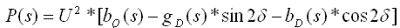
Источник: Заболотный И.П., Гришанов С.А. Метод управления динамическим режимом синхронного генератора с использованием фазовых траекторий движения ротора
// Журнал Електротехнiка i електромеханiка, №1. — Харьков. — 2007. — С. 21–25.
Для управления переходными режимами синхронных генераторов (СГ) в устройствах противоаварийной автоматики (ПА) автоматической системы управления используются алгоритмы, позволяющие оценить зону устойчивости электроэнергетической системы (ЭЭС) либо с помощью функций Ляпунова, либо путем использования уравнений классификационной функции (КФ), определяющей классы «эталонов» устойчивой и неустойчивой работы СГ [1–5]. Однако из–за ряда допущений полученная зона ус-тойчивости меньше реальной, что существенно снижает эффективность управления. Кроме того, суще-ствующие методы не позволяет учитывать особенности стадий переходного процесса путем адаптации математической модели в пусковом органе устройства управления.
В [5] сопоставлены зоны устойчивости генератора типа ТВВ–1000/4, полученные с помощью функций Ляпунова и на основе нелинейного уравнения КФ.
Для распознавания классов ЭЭС используют либо линейное представление решающей функции [3– 4], либо нелинейные зависимости от угла вылета ротора и его производных [5].
Реализация управления переходным процессом СГ включает в себя этап получения (процесс обучения) уравнения КФ. На этом этапе при использовании простейшей модели синхронного генератора выполняются расчеты переходных процессов в ЭЭС при различных величинах возмущений и параметров исходного режима с последующим разделением полученного множества на классы устойчивой и неустойчивой работы СГ и получением параметров уравнения КФ.
Таким образом, на зоны устойчивости СГ влияют не только достоверность математической модели ЭЭС, но и погрешности получения параметров уравнения КФ. Однако преимущество прямых методов оценки устойчивости, удобное определение запасов устойчивости обуславливают их использование.
Как известно, структурная перестройка энергетики и внедрение энергетического рынка сопровождаются нарушением иерархических связей существующей системы управления ЭЭС и, как следствие, наблюдается значительный рост количества технологических задач при управлении электроэнергетическими объектами, их разнообразие и интеграция через динамические ситуации, которые необходимо анализировать. Внедрение микропроцессорной техники в разные системы управления и развитие новых информационных технологий создает условия для построения интегрированных (автоматизированная и автоматическая) систем управления энергетическими объектами. Уровень использования интеллектуальных методов в построении современных устройств ПА позволяет реализовать работу последних, как адаптируемых. Понятно, что эффективность цифровых устройств ПА, особенно обеспечение адаптации модели объекта
к текущему состоянию и учету особенностей протекания переходного процесса во времени, в значительной степени зависит от реализованного метода оценки ситуации ЭЭС.
Таким образом, цель работы — совершенствование методов и математических моделей, как для пусковых органов цифровых устройств ПА, так и для информационно-управляющей системы является актуальной задачей.
Модель пускового органа устройства ПА может быть представлена в виде решающего правила, с помощью которого, не решая систему дифференциальных уравнений, которые описывают процесс в рассмотренной системе, определяются условия устойчивости ЭЭС при возникновении аварийной ситуации. Решающее правило являет собой некоторую аппроксимацию поверхности, которая разделяет в пространстве параметров, которые характеризуют исходный режим ЭЭС и аварийную ситуацию, области устойчивой и неустойчивой работы ЭЭС.
В соответствии с [6] анализ динамической устойчивости выполняется на основании метода площадей с использованием выражения для характеристики угловой мощности и схем замещения нормального, аварийного и послеаварийного режимов Следует отметить, что уравнения могут быть записаны не только через переходную ЭДС генератора (учет АРВ пропорционального типа), а также через синхронную ЭДС (не учет АРВ) и напряжение на шинах генератора (учет АРВ сильного действия).
Для учета физических явлений в роторе генератора предлагается использовать зависимости для асинхронной мощности генератора [7]:
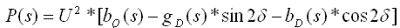
Из условия устойчивости на основании равенства площади ускорения и возможной площади торможения следует, что при достижении углом вылета ротора критического значения скольжения становится равным нулю. Кинетическая энергия, запасенная при разгоне ротора в аварийном режиме, израсходована на торможение после отключения КЗ. Далее изменение угла вылета ротора определяется угловой характеристикой мощности послеаварийного режима. Если параметры исходного режима не меняются и при расчетах не учитывать системы регулирования генератора, зависимости, определяющие поведение генератора в послеаварийном режиме не изменяться.
При рассмотрении нелинейных систем в общем случае найти аналитическое решение не удается, но для простейших схем можно получить не само решение, а уравнение фазовой траектории. Рассмотрим систему уравнений без учета P(s):
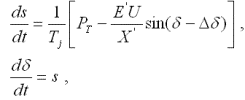
где Е’, U, X’ — переходная ЭДС СГ, напряжение на шинах системы, переходное сопротивление соответственно;
Тj — постоянная инерции агрегата;
s, δ, Δ — скольжение, угол между переходной ЭДС и напряжением, угол между переходной ЭДС и поперечной осью ротора соответственно.
Разделив первое уравнение на второе, найдем уравнение интегральной кривой

Интегрирование уравнения дает
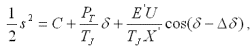
где С — постоянная интегрирования, определенная из начальных условий.
Если коэффициенты уравнения определять по параметрам послеаварийного режима и использовать в качестве начальных условий скольжение (равно нулю) при достижении углом критического угла и значение критического угла, то получим фазовую траекторию послеаварийного режима.
Если коэффициенты уравнения определять по параметрам аварийного режима и использовать в качестве начальных условий скольжение (равно нулю) и угол в предшествующем синхронном режиме, то получим, то получим фазовую траекторию аварийного режима.
Таким образом, на основании данных исходного режима: мощности турбины, начального угла, сопротивлений ЭЭС определяется КФ эталонов устойчивого и неустойчивого режимов.
На основе измерений параметров режима определяется текущее значение угла вылета ротора и это значение сравнивается с предельным по условиям устойчивости и определяется значение КФ.
Предельный угол отключения КЗ возможно определить по формуле при использовании данных аварийного режима (С, Х) и послеаварийного режимов:
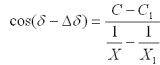
Тенденция к уменьшению КФ свидетельствует о приближении генератора к границе устойчивости. Если принятые меры управления дадут положительный эффект, то значение КФ начинает увеличиваться, в противном случае, при достижении значения КФ равного нулю генератор должен быть отключен.
Метод определения предельного времени отключения КЗ состоит из следующих этапов:
1. Определение уравнений фазовой траектории для послеаварийного режима ЭЭС
2. Определение уравнений фазовой траектории для аварийного режима ЭЭС.
3. Совместное решение уравнение фазовых траекторий для аварийного и послеаварийного режимов. Значение угла вылета ротора и скольжения, которому удовлетворяют обе фазовых траектории, является предельным углом отключения КЗ.
4. Определение предельного угла отключения КЗ по формуле [6]:
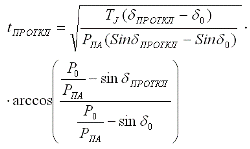
Ниже представлены результаты исследований влияния мощности исходного режима ЭЭС на время отключения КЗ и на классификационную характеристику, разделяющие «эталоны» классов устойчивых и неустойчивых режимов. При этом рассматриваются зависимости s = f(δ) для аварийного и послеаварийного режимов с учетом различных факторов.
Анализировались следующие варианты:
1. Мощность турбины в исходном режиме работы ЭЭС меняется, рассматривается один вид КЗ в одном и том месте, демпферный момент не учитывается, не учитываются переходные процессы в ОВГ: P0=var (0.6…1 о.е.); Pав = const; Pd = 0.
2. Мощность турбины в исходном режиме работы ЭЭС не меняется, меняется вид и место КЗ, демпферный момент не учитывается: P0= const (1 о.е.); Pав = var (0…0.4 о.е.); Pd = 0.
3. Мощность турбины в исходном режиме работы ЭЭС не меняется, не меняется вид и место КЗ, демпферный момент изменяется: P0= const (1 о.е.);
Pав = const (0…0.4 о.е.); Pd = var.