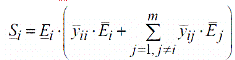
Источник: Научные проблемы транспорта Сибири и Дальнего Востока. —2009.— №1. — 84 – 87
В данной работе, применительно к указанной задаче, рассматривались методы расчета пределов генерируемой в узлах и передаваемой по сечениям сети мощности на основе матрицы собственных и взаимных проводимостей генерирующих узлов.
Традиционный метод получения матрицы СВП ГУ (прямой метод) основывается на преобразовании исходной электрической схемы замещения ЭЭС, требует полной и достоверной информации о топологии и параметрах сети. Сбор, хранение и контроль
данной информации требует значительных временных и материальных затрат. Кроме того, любые коммутации в схеме сети приводят к необходимости внесения изменений в электрическую схему замещения и перерасчета матрицы. Поэтому применение прямого метода в темпе переходного процесса вызывает большие трудности.
Система мониторинга переходных режимов (СМПР (Россия) [2], WAMS (США) [3,4]) позволяет в режиме реального времени контролировать параметры генерирующих узлов ЭЭС и синхронизировать эту информацию по времени, с помощью спутников. Поэтому эти данные могут быть использованы
для идентификации матрицы СВП косвенным методом.
Малый объем информации, необходимый для определения матрицы СВП косвенным методом, отсутствие необходимости в контроле топологии и параметров сети, позволяют использовать косвенный метод расчета в реальном времени процесса, однако недостаточные изученность и необходимость формализации модели создают сложность его применения на практике.
Сопоставление прямого и косвенного методов определения матрицы СВП производилось на примере Тюменской энергосистемы, работающей параллельно с ЭЭС Урала. Связь с энергосистемой осуществляется через Рефтинскую ГРЭС.
При расчетах матрицы СВП приняты следующие допущения:
• генераторы моделируются постоянной переходной ЭДС (Е`) за сопротивлением Х`d;
• местная нагрузка электрических станций представляется постоянным сопротивлением;
Расчет прямым методом проводился в два этапа:
1. Расчет матрицы СВП активных узлов без учета внутренних сопротивлений генераторов. Выполняется на основе уравнений установившегося режима сети путем исключения всех узлов сети, в которых нет генерации.
2. Расчет матрицы СВП для эквивалентных ЭДС генераторных узлов (с учетом внутренних сопротивлений генераторов). Ведется на основе данных, полученных на предыдущем этапе.
Активными узлами считаются ЭДС генераторов.
Для реализации метода, в программной среде MatLAB была со ставлена программа на основе метода исключения Гаусса.
Контроль правильности определения проводимостей, производился путем сравнения мощности генерации узлов, вычисленной на основе полученной матрицы СВП, с данными, полученными в результате расчета установившегося режима по программе MUSTANG.
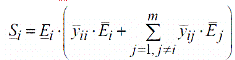
где Si — вектор полной мощности генерации i–ого узла, МВА;
— вектор ЭДС i–ого узла, кВ;
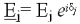— сопряженный вектор ЭДС j–ого узла, кВ;
yii — сопряженный вектор суммы проводимости i–ого узла и взаимных проводимостей i–ого узла с остальными узлами, См;
yij — сопряженный вектор взаимной проводимости i–ого и j–ого узлов, См;
Модули ЭДС ГУ Ej вычислялись по формуле (2):
где Ui — напряжение на шинах ГУ, кВ;
Qi — реактивная мощность генерации, Мвар;
Pi — активная мощность генерации, МВт;
x`di — переходное индуктивное сопротивление генератора, Ом.
Углы вектора ЭДС i E , вычислялись по формуле (3):
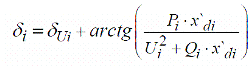
где δ Ui — фаза напряжения i–ого ГУ, град.
Значения параметров Ui , Qi , Pi и δUi брались из результатов расчетов по программе MUSTANG.
В результате расчетов методом исключения Гаусса получена матрица СВП для модели взаимного движения генераторов из пяти эквивалентных генерирующих узлов Тюменской энергосистемы.
Определение матрицы СВП косвенным методом возможно только при наличии относительного изменения углов ЭДС генерирующих узлов. Так, при принятом расчетном возмущении, однофазное короткое замыкание
вблизи Нижневартовской НРЭС, взаимные углы эквивалентных генераторов СГРЭС–1–500, СГРЭС–1–220 и СГРЭС–2 мало изменяются в переходном процессе из-за наличия сильной трансформаторной связи между ними, поэтому в расчетах они замещены одним эквивалентным генератором.
Косвенным методом получена эквивалентная трехузловая схема сети и соответствующая матрица СВП. Первый узел — эквивалентный генератор СГРЭС–1–220, СГРЭС–1–500, СГРЭС–2, второй — НВГРЭС, третий — Рефтинская ГРЭС.
Сопоставление пределов по статической устойчивости, получаемых разными методами производился путем сравнения пределов мощности генерирующих узлов, определяемые по матрице СВП.
Активная мощность, генерируемая узлом, вычисляется по формуле:
где Pi — активная мощность генерации i–ого узла, МВт;
Yii — модуль вектора проводимости ii y , См;
Ψii — угол наклон вектора проводимости ii y , град;
Δi — угол наклона вектора ЭДС i–ого узла, град;
δj — угол наклона вектора ЭДС i–ого узла, град;
Ψij — угол наклона вектора взаимной проводимости i–ого и j–ого узлов.
Максимум выдачи активной мощности происходит при
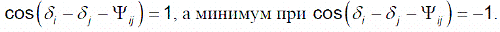
Для станции НВГРЭС расчетное значение максимума выдачи мощности, определенное с помощью матрицы СВП, полученной классическим методом, составило 2598,7 МВт, минимума – 2243,6 МВт.
Расчетное значение максимума выдачи мощности, определенное с помощью матрицы СВП, полученной косвенным методом, составило 2660 МВт, минимума и -2480 МВт.
В результате проведенного исследования сделаны следующие выводы:
1. WAMS–технологии позволяют с достаточной точностью осуществлять идентификацию матрицы СВП ГУ в режиме on–line, что дает возможность контролировать запасы статической устойчивости ЭЭС.
2. Результаты сравнения методов свидетельствуют о возможности контроля запасов статической устойчивости ЭЭС на основе матрицы СВП, получаемой как классическим (прямым) методом, так и косвенным (на основе регистрации переходных процессов).