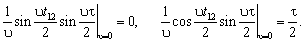УДК 621.311.1.018.3
ОСОБЛИВОСТІ АНАЛІЗУ ІНТЕРГАРМОНІК
О. М. ДМИТРІЄВА (канд.техн.наук, доц.), І.Б. ПОНОМАРЬОВ
Донецький національний технічний університет
Источник: Наукові праці Донецького національного технічного університету, с. 48-51.
Розглядається задача оцінювання несинусоїдальності напруги при наявності неканонічного та безперервного спектрів. Вказується область коректності використання інтергармонік. Аналізуються похибки використання стандартної процедури обробки осцилограм напруги.
Рассматривается задача оценивания несинусоидальности напряжения при наличии неканонического и непрерывного спектров. Указывается область корректности использования интергармоник. Анализируются ошибки использования стандартной процедуры обработки осциллограмм напряжения.
The estimation task of voltage nonsinusoidality in the presence of not canonical and continuous spectrum is considered. The area of a correctness of interharmonics usage is indicates. Errors of usage of standard processing procedure of voltage oscillograms are analyzed.
Ключові слова: ЕМС, несинусоїдальність, гармоніки, спектральна щільність, похибки оцінювання ЕМС
Ключевые слова: ЭМС, несинусоидальность, гармоники, спектральная плотность, ошибки оценивания ЭМС
Key words: EMC, nonsinusoidality, harmonics, spectral density, errors of EMC estimation
Постановка задачі. Інтергармоніки являють собою синусоїдальні процеси зміни за часом миттєвих значень и напруги, частота яких відрізняється від частоти 50 Гц у меншу або більшу сторони [1]. У проектуванні використовуються періодичні графіки u(t), по яких розрахунок будь-яких гармонік виконується шляхом розкладання в ряд Фур’є за час тривалості циклів. У діючих електричних мережах такої ясності немає, оскільки стандарт [2] передбачає визначення тільки вищих гармонік різними вимірюваними вікнами у широкому діапазоні їх ширини: від 0,08 до 0,5 с. В [3] показано, що такий підхід не забезпечує достовірності оцінок ЕМС за вищими гармоніками.
Метою статті є узагальнення результатів [3] на інтергармоніки. Для визначеності розглядається стандартна процедура цифрової обробки осцилограм з використанням прямокутного вікна шириною к = 0,32 с без пробілів між вікнами (табл. Е.1 з [2]).
Прийняті наступні терміни і позначення. Для канонічних f-гармонік: n – порядок гармоніки, fn – і ωn – частота в Гц і кутова частота в рад/с, сn – амплітуда n-ої гармоніки. Для інтергармонік (ν-гармонік): m – номер (не порядок) гармоніки, νm і Ωm = 2πνm – частоти і кутові частоти, сm – амплітуди. Окрім того, для періодичного процесу з тривалістю циклу Тμ використовуються μ-гармоніки з основною частотою μ1 = 1/Tμ, порядком r, частотами μr і ωμr = 2&piμr, амплітудами сμr. При обробці за стандартною процедурою і k ≠ Tμ гармонічні складові формально розрахувати можна, але вони не мають смислу. Тому будемо називати їх квазігармоніками [3] або k-гармоніками, які мають основну частоту β1 = 1/k = 3.125 Гц, порядок q, частоти βq і ωβq = 2πβq, амплітуди сβq.
Періодичні процеси. Для наочності розглянемо суму
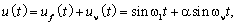 (1)
(1)
перша (корисна) складова якої має частоту f1 = 50 Гц і одиночну амплітуду, а друга є завадою – інтергармонікою з частотою ν і амплітудою α < 1. Якщо частота завади є раціональним числом, то процес (1) буде періодичним, тривалість циклу Тμ якого залежить від співвідношення частот f1 і ν. При ірраціональній частоті процес буде неперіодичним.
Слід відзначити, що мале змінення частоти інтергармоніки може приводити до значного змінення тривалості циклу. Наприклад, при ν = 4 Гц цикл Тμ = 0,5 с, а при близькій частоті √16,1 = 4,012 Гц він є нескінченним.
Нехай перетворення Фур’є процесу (1) здійснюється на відрізку часу від t1 до t2 тривалістю τ = t2 – t1. Позначивши через р порядок відповідних гармонік, γ1 = 1/τ – основну частоту, ωγ1 = 2πλ1 – основну кутову частоту, t1,2 = t1 + t2, υ1,2 = ω1 ± pωγ1, υ3,4 = Ω1 ± pωγ1, отримаємо коефіцієнти ряду Фур’є при р ≥ 1 і будь-якому ± ≠ 0:
 (2)
(2)
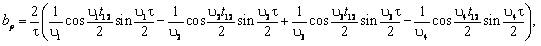 (3)
(3)
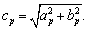 (4)
(4)
Якщо ν = 0, то враховуючи, що границя sin(x)/x → 0 при х → 0 дорівнює одиниці, відповідні члени в (2)-(4) становлять:
Постійний член ряду при р = 0 становить c0 = a0/2.
Формули (2)-(4) є загальними для гармонік будь-якого виду: при τ = 0,02 с і р = n вини дають вищи гармоніки, при τ = Тμ і р = r – μr-гармоніки, при τ = k і p = q – квазігармоніки.
Якщо τ = Тμ і Тμ < ∞, формули (2)-(4) дають дві гармоніки з амплітудами 1 і α, порядками r = fTμ і μTμ, частотами μr = fTμμ1 = f і νTμμ1 = ν. Це означає, що розв’язок є точним. Але для цього потрібно знати, що процес є періодичним з циклом Тμ. При використанні ж аналізаторів якості напруги графік u(t) не записується, тому інформація про Тμ відсутня – приводяться лише результати обробки по вікнах. Очевидно, що лише для окремих випадків, коли цикл Тμ ≤ 0,32 с і ціле число разів розміщується в інтервалі 0,32 с, результат буде вірним. Проте такі випадки зустрічаються зовсім не часто.
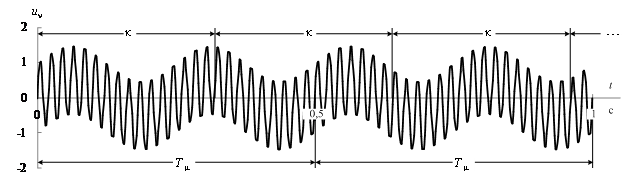
Проілюструємо механізм виникнення помилок на прикладі інтергармоніки частотою 4 Гц з періодом tν = 1/ν = 0,25 c і амплітудою α = 0,5. Сумарний процес (1) має цикл Тμ = 0,5 с, у якому розміщується 25 циклів tf = 0,02 с і два цикли інтергармоніки (рис. 1). Тривалість 0,32 с не співпадає з Тμ, тому графіки у вікнах будуть різними. На рис. 2 потовщеними лініями показано фактичний спектр, а світлими кружками для першого вікна частково представлені спектри «гармонік», які розраховані за формулами (2)-(4) при τ = k. Згідно з [2] враховувалися гармоніки з амплітудами, більшими ніж 0,001: для трьох послідовних вікон включно до q = 156; 216; 76 з частотами до 487,5; 675; 237,5 Гц. Оскільки на інтервалі 0,32 с цикл 0,02 с розміщується ціле число разів, амплітуда гармоніки 50 Гц (q = 16) визначається точно. Інтергармоніка частотою 4 Гц відсутня – її потужність розподілилася по частотах 3,125 і 6,25 Гц (q = 1 і 2). З’явилися постійні складові (q = 0), вищі гармоніки (q = 32; 48; …) і квазігармоніки . Спектр гармонік змінюється від вікна до вікна, хоча фактично він є постійним.
Рисунок 1 – Сума гармонічних сигналів з частотами 50 і 8 Гц
Аналогічно стоїть справа і з періодичними коливаннями напруги. Наприклад, ідеалізоване гармонічне коливання з частотою λ << 50 Гц приблизно описується виразом, до якого входить не тільки несуча частота 50 Гц, але і дві інтергармоніки з частотами 50 &plusm; λ. Тривалість циклу Тμ залежить від співвідношення частот 50 Гц і λ: наприклад, при λ = 25 Гц маємо Тμ = 0,04 с, а при 27 Гц – 1 с. При великих частотах (практично λ > 6 Гц) у циклі 20 мс з’являються інші гармоніки, які модулюються частотою λ, тому фактичний спектр гармонік значно збільшується.
Рисунок 2 – Спектри гармонік: точний і визначений на інтервалі 0 ≤ t ≤ 0,32 с
Неперіодичні процеси.У діючих електричних мережах процес u(t) є випадковим, для якого поняття «гармоніка» не має смислу. Він описується спектральною щільністю, яка має великий максимум на частоті 50 Гц і може мати максимуми на інших частотах. Оскільки в [2] показники несинусоїдальності нормуються окремо від складової 50 Гц, з процесу u(t) доводиться виділяти несинусоїдальну складову uν(t) шляхом пропускання u(t) через вузькосмуговий фільтр з частотою настройки 50 Гц, або поциклічним виділенням синусоїди 50 Гц на інтервалах 0,02 с.
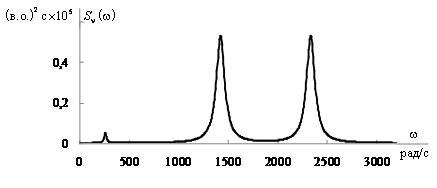
Проаналізуємо похибки, які виникають при обробці осцилограм за стандартною процедурою на прикладі несинусоїдальної складової напруги на шинах 6 кВ електросталеплавильного цеху. Спектральна щільність Sν(ω) цієї складової представлена на рис. 3. Для можливості зіставлення з обробкою по вікнах щільність розраховувалася за час 0,32 с. У діапазоні частот від ωм = 60 до ωМ = 3500 рад/с вона добре апроксимується виразом
 (5)
(5)
де величини σν1 = 0,03483, σν2 = 0,02142 вимірюється у відносних одиницях (в.о.), а параметри становлять: k = 1,382, α1 = 50, α2 = 14 с–1, ω01 = 2330, ω02 = 1420, ω03 = 258 рад/с. За цими межами щільність дорівнює нулю.
Рисунок 3 – Спектральна щільність несинусоїдальної складової напруги на шинах підстанції 6 кВ
У межах (ωм, ωМ) щільність є безперервною функцією і при ω = 0 дорівнює нулю. Однак розкладання на квазігармоніки дає дискретний спектр з постійною складовою, що не відповідає дійсності.
Якщо тривалість часу, за який розраховувалася спектральна щільність, не співпадає з 0,32 с, то спектр квазігармонік буде змінюватися від відрізку до відрізку по 0,32 с.
Вплив на електроприймачі.Похибки у визначенні спектрів приводять до похибок у оцінюванні впливу несинусоїдальності напруги на електроприймачі. Для короткості розглянемо три ідеальні електроприймачі з активною, індуктивної і ємнісною провідністями (індекси R, L і С), показниками ЕМС яких є ефективні значення IRe, ILe і ICe несинусоїдальних складових відповідних струмів.
При активній провідності у в.о. струм і напруга співпадають. При індуктивній провідності для отримання в.о. струму напругу потрібно розділити на відносну величину частоти ν* = ν/50 або ω = ω*/100π, а при ємнісній – помножити на ту ж саму величину. З урахуванням цього для процесу (1) маємо
 (6)
(6)
Якщо ж використовувати квазігармоніки з відносними частотами βq* = βq/50, то виключаючи складові з частотою 50 Гц (при q = 16), на кожному інтервалі по 0,32 с отримаємо:
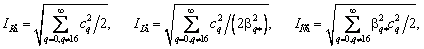 (7)
(7)
де враховано, що при постійній напрузі, коли q = 0, ємнісний струм дорівнює нулю.
При ν = 4Гц і α = 0,5 згідно з (6) точні значення дорівнюють: IRe = 0,3536; ILe = 4,4194 і ICe = 0,0283, у той час як на перших трьох інтервалах IRe = 0,353; 0,340; 0,365; ILe = ∞; ICe = 28,17; 44,42; 12,32. Різницю у результатах оцінювання ЕМС найбільш наочно видно на струмі через індуктивність, який при появі постійної складової, що не існує, стає нескінченним. Для випадкових завад струми визначаються за спектральною щільністю:
 (8)
(8)
Інтегрування щільності виду (5) здійснюється у межах від ωм до ωМ. Усі інтеграли є табличними, але кінцеві вирази є громіздкими. Наприклад, квадрат ефективного значення струму крізь індуктивність становить
 (9)
(9)
де позначено: 

Вираз (9) дає кінцеву величину ефективного струму, тоді як розрахунки по квазігармоніках на інтервалах по 0,32 с, як і для періодичних процесів, дають постійні складові, а отже нескінчений струм.
Розглянуті приклади показують, що квазігармоніки не можна використовувати для оцінювання впливу на електроприймачі, а також для нормування завад на їх затискачах. Останнє доцільно виконувати шляхом встановлення норм на підвищення температури, як у [4], або з використанням стандартних електроприймачів: за дозами несинусоїдальності [3].
Висновки.
- Використання інтергармонік є коректним лише для періодичної завади з тривалістю циклу, що не співпадає з 0,02 с.
- Показники ЕМС за «гармоніками», які нормуються у ГОСТ 13109-97 у точках загального приєднання, є умовними і не можуть використовуватися для оцінювання впливу несинусоїдальності напруги на електричні мережі та електроприймачі.
- У якості показників ЕМС для електрообладнання доцільно прийняти низько- і високочастотну дози несинусоїдальності без нормування «гармонік».
- Жежеленко И.В. Высшие гармоники в системах электроснабжения промпредприятий /И.В. Жежеленко. – М.: Энергоатомиздат, 2000.
- ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
- Куренный Э.Г. Оценка несинусоидальности напряжения при анализе качества электроэнергии / Э.Г. Куренный, А.П. Лютый // Электричество, 2005, № 8.
- ГОСТ 183-74. Машины электрические вращающиеся. Общие технические требования. – Введ. 01.01.76.