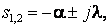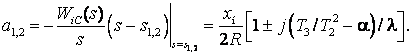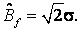Оценка несинусоидальности напряжения

КУРЕННЫЙ Э.Г., ЛЮТЫЙ А.П.

---

Источник: Журнал «Электричество», 2005 г., №8.

---

Рассматривается проблема обеспечения достоверности и универсальности показателей несинусоидальности. Предлагается оценивать ЭМС путем моделирования воздействий несинусоидальности на электрооборудование. Для целей нормирования вводятся понятия низко- и высокочастотной доз несинусоидальности.

К л ю ч е в ы е с л о в а : ЭМС, несинусоидальность, гармоники, модели ЭМС, дозы несинусоидальности.

The problem of guarantee of reliability and universality of nonsinusoidality indexes is considered. For estimation of EMC by modeling of nonsinusoidality influences on electrical equipment is proposed. For the purpose of standardization the conceptions of low- and high-frequency doses of nonsinusoidality are introduced.

K e y w o r d s: EMC, nonsinusoidality, harmonics, EMC models, dose of nonsinusoidality.

Постановка задачи. Несинусоидальность напряжения является одним из часто встречающихся видов кондуктивных помех для электромагнитной совместимости (ЭМС). Показатели ЭМС должны иметь физический смысл, быть применимыми для помех и_v(t) любого вида (периодических или случайных), обеспечивать единство их нормирования, измерения и расчета.

Существующие методы оценки ЭМС по показателям, основанным на понятии гармоник, для случайных помех этим очевидным условиям не удовлетворяют, что требует разработки универсальных показателей ЭМС по несинусоидальности напряжения.

Концептуальным является принцип оценки ЭМС путем моделирования воздействий помехи на электрооборудование [1]. В полной мере этот принцип реализован в нормировании доз фликера напряжения [2-5], поэтому далее будет проводиться аналогия с фликер-моделью, включая название ее блоков.

Будем различать два типа задач оценки ЭМС. В задачах первого типа получают данные для определения ущерба от несинусоидальности, что требует моделирования конкретного электрооборудования и использования физически обоснованных показателей ЭМС, отражающих негативные последствия искажений кривой напряжения.

В задачах второго типа устанавливаются нормы на показатели ЭМС, которые используются во взаимоотношениях между энергоснабжающей организацией и потребителем в точке коммерческого контроля качества электрической энергии. Здесь невозможно учесть особенности всего электрооборудования, поэтому нормируемые параметры в общем случае не могут быть использованы для решения задач первого типа.

Показатели ЭМС. Модели ЭМС должны быть простыми, но вместе с тем отражать основные свойства объектов. Обобщенно модель можно представить взвешивающим фильтром ВФ (термин из [3]) и энергетическим блоком БЭ (рис. 1). ВФ моделирует реакцию i(t) объекта на помеху (во фликер-модели – адаптация зрения [4]). Негативные последствия от воздействия помехи зависят от мощности реакции и инерционности объекта. Поэтому самый простой энергетический блок должен иметь квадратор 1 и инерционное звено первого порядка 2 (блок квадратичного инерционного сглаживания в [3]). Показатель ЭМС устанавливается по характеристикам энергетического инерционного процесса на выходе энергетического блока (зрительное ощущение в [3]), но не по характеристикам помехи.

Несинусоидальность вызывает дополнительный нагрев электрооборудования, зависящий от квадратов тока. В связи с этим ВФ моделирует проводимость электрооборудования, а реакцией является ток. Постоянная времени инерционного звена совпадает с постоянной времени нагрева Т объекта. Одна и та же помеха вызывает тем меньший нагрев, чем больше тепловая инерция. Это еще раз подчеркивает некорректность оценки ЭМС по характеристикам и_v(t) без моделирования объекта.

Рис.1

Физический смысл энергетического инерционного процесса ω_vT(t) состоит в том, что он пропорционален температуре нагрева электрооборудования. Максимальная температура не должна превышать допустимую. Если это техническое требование к ЭМС нарушается, то эксплуатация оборудования невозможна. Для определения ущерба от несинусоидальности необходимо оценивать кратность снижения срока службы электрооборудования и дополнительные потери активной мощности. Эти величины определяются через средние значения θ_с температуры, инвариантные к постоянным времени нагрева.

Потери активной мощности, максимальное и среднее значения температуры или квадратичного инерционного процесса являются физически обоснованными показателями ЭМС и удовлетворяют всем сформулированным ранее требованиям.

Немодулированные процессы. Поскольку электроэнергия передается на частоте f = 50 Гц, процесс u(t) изменения текущих значений напряжения (или тока) естественно представить в виде суммы двух компонент: синусоидальной u_f(t) с частотой 50 Гц и несинусоидальной

u_v(t) = u(t) − u_f(t)               (1)

которые будем называть синусоидой и помехой.

При отсутствии низкочастотной модуляции амплитуда В_f синусоиды

u_f(t) = B_fsinω_ft               (2)

не изменяется в пределах длительности t_f = 1 / f любого цикла, где ω_f = 2πf – несущая угловая частота.

В проектировании допущение об отсутствии модуляции принимается всегда, а несинусоидальная компонента, периодическая или случайная, рассчитывается по токам источников помех – электроприемников с нелинейными вольт-амперными характеристиками. В действующих сетях соотношение (2) корректно, если нет колебаний напряжения.

В случае периодической помехи напряжение можно представить в виде ряда Фурье

u(t) = u_1Ф(t) + u_n∑(t),

который содержит первую гармонику u_1Ф(t) и сумму u_n∑(t) канонических гармоник с порядком n≥2. Подставив это выражение в (1), получим соотношение

u_ν(t) = u_1Ф(t) – u_f(t) + u_n∑(t).

Отсюда следует, что несинусоидальная компонента совпадает с суммой высших гармоник лишь при равенстве u_1Ф(t) и u_f(t), которое выполняется далеко не всегда. Проиллюстрируем это на следующем примере. Пусть в синусоиде (2) источник помехи создает провал

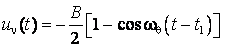               (3)

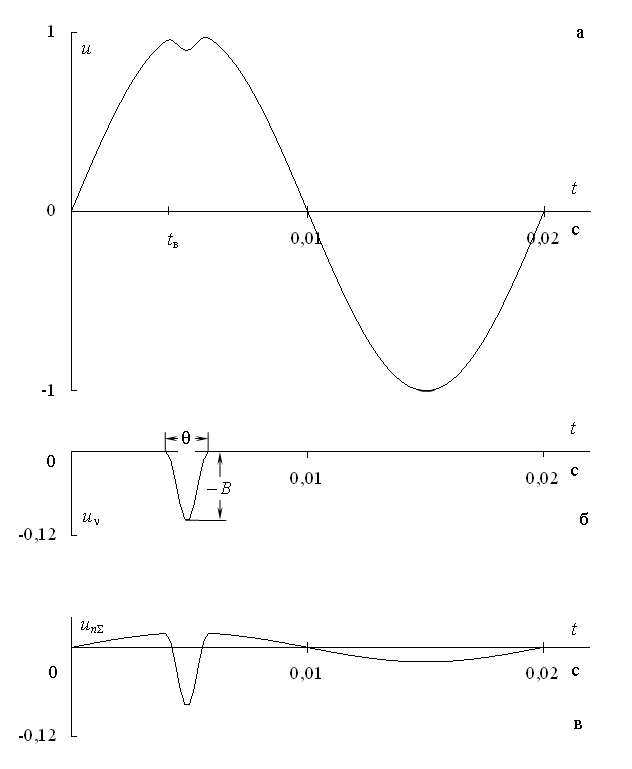
глубиной В и шириной θ, середина которого приходится на вершину синусоиды (рис. 2,а), где t1 – момент начала провала, ω_θ = 2π/θ.

Очевидно, что искажение синусоиды происходит только в области провала, поэтому график несинусоидальной компоненты имеет вид, показанный на рис. 2,б.

Амплитуда основной канонической гармоники u_1Ф(t) определяется выражением

               (4)

при θ* = θ/t_f и В* = В/В_f, а фаза равна нулю.

Рис. 2. Иллюстрация различия между несинусоидальной компонентой (б) и суммой канонических гармоник (в) при В_f = 1, В = 0,1, θ = 0,0018 с

В общем случае амплитуда и фаза зависят от положения провала. Вычитанием основной гармоники из исходного процесса получим график суммы

u_n∑(t) = u(t) – u_1Ф(t).

высших гармоник (рис. 2,в), который принципиально отличается от несинусоидальной компоненты (3): «помеха» якобы имеется в продолжение всего цикла и вызывается двумя провалами (отрицательные области) и двумя выбросами (положительные области), хотя в действительности есть только один провал.

В общем случае синусоида и помеха коррелированы. Например, для периодического процесса на рис. 2,а, который можно рассматривать как стационарный неэргодический процесс, корреляционный момент

               (5)

Гармоники же не коррелированы между собой. Действительно, хотя n-я гармоника с амплитудой В_n и фазой φ_n функционально связана с основной:

u_n = B_nsin[narcsin(u₁/B₁) – φ₁] + φ_n,

но момент взаимной корреляции между ними равен нулю. Это позволяет суммировать квадраты действующих значений гармоник.

В действующих сетях выделить синусоиду можно, если кривая напряжения имеет четко выраженные неискаженные участки синусоиды. На этих участках определенные по любым парам ординат параметры синусоиды остаются неизменными. Несинусоидальная компонента определяется согласно (1). При отсутствии неискаженных участков задача выделения синусоиды не имеет точного решения. В связи с этим необходимо оценивать влияние на электрооборудование всего процесса u(t) или в качестве несинусоидальной компоненты ориентировочно принимать сумму высших гармоник, если помеха периодична.

Для случайных помех понятие гармоники отсутствует, поэтому говорить о сумме высших гармоник некорректно. Тем не менее, при принятом допущении об отсутствии модуляции синусоиду u_1Ф(t) можно выделять по формулам коэффициентов ряда Фурье при n = 1. Разность между u(t) и этой синусоидой дает ориентировочный график несинусоидальности.

Одним из расчетных приемов, используемых в практике, является представление непериодических процессов в виде ряда Фурье на конечном интервале Т_μ (в [2] – 0,32 с) – в предположении, что до и после рассматриваемого интервала процесс периодически повторяется с длительностью цикла Т_μ и основной частотой ω_μ1 = 2π/Т_μ. Обозначим порядок слагаемых ряда через μ и назовем их «квазигармониками». Такой прием возможен, если требуемая для решения задачи длительность процесса меньше периода разложения. При этом следует учитывать все квазигармоники, а не только с частотами, кратными ω_f. В самом деле, если длительность t_f целое число m раз укладывается в Т_μ, то часть квазигармоник будет иметь частоты, совпадающие с частотами канонических гармоник: при μ = mn. Если отношение Т_μ/t_f не будет целым числом, то квазигармоники с частотами ω_n будут отсутствовать. В первом случае учет только квазигармоник с частотами канонических существенно занижает уровень помехи, а во втором будет сделан неверный вывод об отсутствии искажений.

При отсутствии низкочастотной модуляции процесс u_1Ф(t) можно определять как по каждому циклу, так и за весь период Т_μ. Разность между u(t) и u_1Ф(t) синусоидой дает сумму всех квазигармоник, за исключением гармоники с порядком μ = n.

В действующих сетях анализаторы «гармоник» измеряют эффективные значения процессов на выходе узкополосных фильтров. Очевидно, что они совпадают с действующими значениями канонических гармоник лишь при периодических помехах. При непериодических же помехах эффективные значения наблюдаются на любой частоте ω. Будем именовать их «псевдогармониками». Они могут иметь любой «порядок» ν = ω/ω_f, в том числе и дробный.

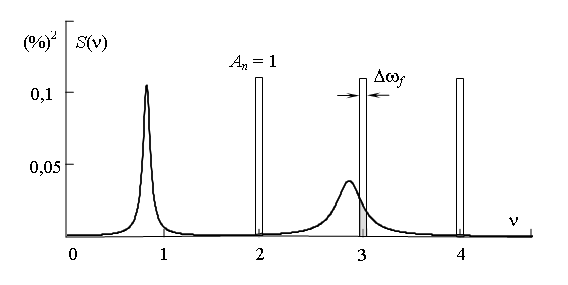
Если учитывать только псевдогармоники с кратными nω_f частотами, принимая их за канонические гармоники, то результаты оценки ЭМС будут существенно занижены. В самом деле, случайные помехи характеризуются спектральной плотностью S(ω) в (%)²*с или S(ν) в (%)². При измерении псевдогармоник из спектральной плотности вырезаются узкие области частот, в пределах которых определяются действующие значения процессов на выходе фильтра. На рис. 3 показаны области на частотах n псевдогармоник, вырезаемые идеальным фильтром с полосой пропускания Δω_f. Если амплитудно-частотная функция (АЧФ) А_n(ω) фильтра в этой полосе равна единице, то дисперсия суммы квазигармоник определяется суммой затушеванных площадей, в то время как на самом деле дисперсия помехи равна площади под всей кривой.

Рис.3 – Спектральная плотность несинусоидальной компоненты напряжения на шинах 6 кВ при работе дуговой сталеплавильной печи

Рассмотренные примеры иллюстрируют условность понятия несинусоидальности. В самом деле, качественно под несинусоидальностью следует понимать такую компоненту, устранение которой делает кривую напряжения синусоидальной. Но этого эффекта, например, для периодических помех можно добиться как устранением процесса u_ν(t), так и u_n∑(t) – различие будет только в амплитудах: во втором случае амплитуда синусоидального напряжения меньше на величину разности между B_f и B_fФ. Принятие той или иной трактовки несинусоидальности зависит от конкретных условий задачи: возможность получения исходной информации, вид корректирующих устройств (активные или пассивные). Методы же оценки ЭМС от этого не изменяются.

Модулированные процессы. Наличие колебаний напряжения принципиально усложняет задачу, так как модуляция сигнала 50 Гц приводит к искажению синусоиды даже при отсутствии источников помех. Например, если в сети наблюдаются гармонические колебания напряжения с размахом δU_t и частотой λ в Гц, то мгновенные значения напряжения определяются выражением

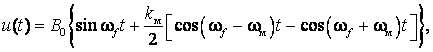               (5)

где В₀ – среднее значение огибающей амплитуд напряжения за период 1/λ k_m = √2δU_t/B₀ – коэффициент модуляции, ω_м = 2πλ. В любом цикле t_f кривая напряжения отличается от синусоиды: слагаемые с боковыми частотами представляют собой интергармоники. В [3] учитываются гармонические колебания частотой от 0,5 до 25 Гц, поэтому соответствующие частоты интергармоник будут равны 49,5 и 50,5 Гц, 25 и 75 Гц. Периодические колебания напряжения другой формы создают теоретически бесконечное количество интергармоник.

Источники периодических помех также могут помимо канонических создавать и интергармоники, в том числе и субгармоники. При случайных колебаниях напряжения понятие интергармоники лишено смысла, а искажения синусоиды наблюдаются во всем частотном диапазоне.

В [2] при наличии колебаний нагрузки рекомендуется использовать быстрое преобразование Фурье, используя прямоугольное окно или окно Хеннинга разной ширины Т_μ (в [2] – Т_w). В отличие от немодулированных процессов такой способ нельзя использовать для выделения синусоиды 50 Гц. Покажем это на простом примере. Пусть за время Т_μ искажение синусоиды произошло только в одном цикле длительностью t_f. Однако синусоида с частотой ω_f (квазигармоника порядка μ = m) относится ко всему периоду Т_μ. Вычтя ее из кривой u(t), получим «несинусоидальную компоненту», которая якобы присутствует во всех циклах, что противоречит физическому смыслу, так как фактически искажение есть только в одном из них.

Лучший результат получается, если выделять синусоиду не на всем интервале, а поциклично. В этом случае график помехи отличен от нуля в пределах тех циклов, где есть искажения. Параметры синусоид в каждом цикле могут быть разными, что приводит к появлению скачков на границах циклов. Их устраняют путем принятия на границе одной ординаты, равной полусумме ординат скачка. В приложении приведен инженерный метод выделения помехи.

Формулы для коэффициентов ряда Фурье предполагают периодичность процесса, в частности, равенство ординат в начале и конце цикла. В случае непериодической помехи эти ординаты могут не совпадать, что приводит к погрешности в определении фазы синусоиды. Для устранения погрешности фазу необходимо варьировать до тех пор, пока не будет достигнут минимум среднеквадратичных отклонений исходного процесса от синусоиды. Необходимость уточнения фазы усложняет расчеты, поэтому целесообразно амплитуду и фазу сразу определять методом наименьших квадратов.

Доля несинусоидальности. На электрооборудование воздействует процесс u(t). Для того, чтобы оценить долю несинусоидальности, необходимо определить параметры ЭМС при совместном воздействии синусоиды и помехи, а затем сопоставить их с параметрами ЭМС от неискаженной синусоиды. Покажем, что в общем случае несинусоидальная компонента не может рассматриваться отдельно от синусоиды. Компонентами входного процесса являются процессы (1) и (2), а компонентами реакции ВФ – соответствующие составляющие i_f(t) и i_ν(t) тока. В силу линейности ВФ эти компоненты можно анализировать раздельно.

Синусоида имеет нулевое среднее значение, поэтому ее эффективное (действующее) значение I_fэ совпадает со стандартом σ_fi. Среднее значение i_νc помехи не всегда равно нулю, вследствие чего эффективное значение определяется по формуле

,

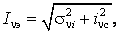где σ_νi – стандарт несинусоидальной компоненты.

Инерционное звено в энергетическом блоке осуществляет линейное преобразование L_T, но квадратор делает БЭ нелинейным. В результате в энергетическом процессе

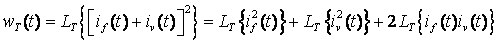               (6)

уже нет явного разделения на две компоненты w_Tf(t) и w_Tν(t).

Чтобы найти эти компоненты, надо третье слагаемое разделить между двумя другими, введя коэффициенты разделения ρ_f и ρ_ν. Тогда

               (7)

Точно так же обстоит дело и с эффективным значением I_э тока. С учетом формулы для дисперсии суммы коррелированных процессов получим

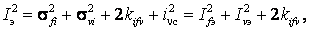               (8)

где k_ifν – момент взаимной корреляции между компонентами тока.

По аналогии с (7) запишем выражения для средних значений компонент энергетического процесса

,

которые пропорциональны средним значениям θ_fc и θ_νc компонент температуры.

Относительная погрешность в определении компоненты θ_νc средней температуры или квадрата эффективного значения тока при раздельном рассмотрении несинусоидальности составит

.

При положительной (отрицательной) корреляции средняя температура занижается (завышается), а при отсутствии корреляции – определяется точно. Последний вывод не относится к максимальной температуре.

Коэффициенты разделения можно принимать из разных соображений. На наш взгляд, это целесообразно сделать по квадратам эффективных значений компонент:

               (10)

Итак, раздельное рассмотрение компонент не обеспечивает достоверности оценки ЭМС. Оно возможно, если вторые слагаемые в выражениях (7) будут мало отличаться от нуля. В общем случае это условие выполняется при I_νэ²/I_fэ²<<1, когда ρ_u≈1 и ρ_ν≈0, а в частном случае определения параметров ЭМС по средним значениям компонент энергетического процесса – если попарно взятые произведения средних значений компонент и все моменты взаимной корреляции равны нулю, т.е. когда выражение в скобках обращается в нуль. В силу линейности ВФ все соображения относительно корреляционных моментов k_fν напряжений справедливы и для корреляционных моментов компонент тока.

Нормирование. Теория и практика нормирования проходят путь от норм на показатели помехи до норм на показатели ЭМС, отражающие воздействие помехи на «стандартный» электроприемник. Например, вначале нормировались размахи и частоты колебаний напряжения, а затем перешли к физически обоснованному параметру – дозе фликера, причем во фликер-модели принята стандартная лампа накаливания мощностью 60 Вт [3].

Таким образом, принцип моделирования распространяется и на задачу второго типа с тем непринципиальным отличием, что условность норм позволяет принять некоторые упрощающие допущения. Во-первых, как и в существующей практике, можно принять раздельное нормирование помех. Тем самым предполагается некоррелированность помех между собой и синусоидой. Во-вторых, поскольку постоянные времени нагрева силового электрооборудования велики, оценку ЭМС достаточно выполнять по эффективному току I_ρэ выбранного стандартного электроприемника от несинусоидальной компоненты.

Введем понятие дозы несинусоидальности

ψ_ν = k_νI_νэ,               (11)

где k_ν – коэффициент пропорциональности. Физический смысл дозы состоит в том, что ее квадрат отражает дополнительные потери мощности в стандартном электроприемнике, а следовательно, его средний перегрев и сокращение срока службы.

Коэффициент пропорциональности выберем таким образом, чтобы допустимое значение дозы ψ_ν = 1. Если известно допустимое значение I_νэ несинусоидальной компоненты тока, то это условие выполняется, когда

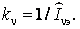               (12)

Обычно же задается допустимое увеличение тока от двух компонент. Принимая за 100 % номинальный ток, из (8) при нулевом коэффициенте корреляции получим соотношение

из которого найдем

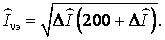               (13)

В действующих сетях помехи могут иметь широкий частотный диапазон (рис. 3). В низкочастотном диапазоне (условно – менее 50 Гц) несинусоидальность более всего сказывается на электроприемниках с индуктивной нагрузкой, а в высокочастотном – на конденсаторных установках и изоляции. Поэтому надо ввести два стандартных электроприемника и две дозы несинусоидальности: ψ_νl – низкочастотную и ψ_νh – высокочастотную.

Выбор стандартных электроприемников и их параметров должен осуществляться путем экспертных оценок, что требует отдельного рассмотрения. Проиллюстрируем выбор такого электроприемника на примере высокочастотной дозы.

Простейшая схема замещения конденсатора содержит активное сопротивление r и индуктивность L проводников, а также две параллельные ветви с сопротивлением R и емкостью С диэлектрика [6]. Полная проводимость

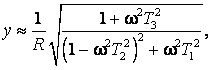               (14)

где Т₁≈rC, Т₂²≈LC, Т₃ = rC и учтено, что R >> r.

Выразим проводимость в относительных единицах, умножив ее на номинальное сопротивление х_н конденсатора. Для согласования с параметрами схемы замещения при частоте ω_f должно быть ух_н = 1. Тогда из (14) получим

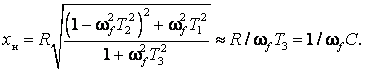               (15)

Схема замещения представляет собой структурную схему ВФ с передаточной функцией

               (16)

Отсюда следует, что ВФ состоит из трех элементарных звеньев: 4 – пропорционального с коэффициентом передачи х_н/R, 5 – колебательного с постоянными времени T₁ и T₂, 6 – форсирующего с постоянной времени T₃ (рис. 4). На вход ВФ поступает несинусоидальная компонента напряжения, которая выделяется из входного напряжения в блоке 1. На выходе ВФ наблюдается несинусоидальная компонента тока. В энергетический блок БЭ входит квадратор 1 и инерционное звено 2 с большой постоянной времени. В блоке 7 из I_νэ² извлекается квадратный корень и результат умножается на коэффициент kh, значение которого выберем из условия длительно допустимой перегрузки конденсатора.

Рис. 4. Структурная схема модели ЭМС стандартного конденсатора

Стандарт [7] допускает длительную работу при нагрузках до 1,3 от номинального тока, но не указывает, насколько меньше 1,3 она может быть. Принимать значение 1,3 в качестве длительно допустимого нельзя, так как в этом же стандарте повышение напряжения, а следовательно тока, на 30 % допускается лишь в течение 1 мин. Для определенности примем длительно допустимую перегрузку равной 10 %, что соответствует норме повышения напряжения на 10 %, которое допускается в течение 12 ч, т.е. практически длительно. Подстановка этого значения в (12) и (13) дает I_νэ = 45,83 % и kh = 0,0218 (%)^–1.

Максимальное значение ψ_hmax дозы несинусоидальности определяется с интегральной вероятностью 0,95. Условие ЭМС:

ψ_hmax ≤ 1.               (17)

В качестве стандартного можно принять силовой конденсатор 18 квар, 400 В с найденными из опыта параметрами [6]: r = 6,88*10^–3 Ом, R = 2,69*10⁸ Ом, L = 2,7*10^–7 Гн, С = 5,84*10^{–4,/sup> Ф. В этом случае T₁ = 4,018*10–6 с, T₂ = 1,256*10–5 с, T₃ = 1,571*105 с, х_н = 5,45 Ом.}

Аналогичным образом выбирается стандартный электроприемник и для низкочастотного диапазона. На наш взгляд, это должен быть асинхронный электродвигатель. Для целей нормирования можно принять предложенную в [8] для ориентировочных оценок модель ЭМС в виде инерционного звена первого порядка с коэффициентом передачи а_д = 2,27 и постоянной времени T_д = 0,0019 с.

В стандарте на электрические машины нормируются длительно допустимая температура θ_N и ее допустимое превышение Δθ. Ввиду малости диапазонов изменения температур, относительное приращение температуры в два раза превышает относительное приращение тока. Это позволяет определить допустимое увеличение тока в процентах:

Примем значения допустимых температур для изоляции класса А: θ_N = 65 °С и Δθ = 10 °С. В этом случае согласно (13) несинусоидальная компонента тока не должна превышать 40 %. При этом коэффициент k_νl = 0,025 (%)^–1.

Для помехи со спектральной плотностью, приведенной на рис. 3, эффективные токи стандартного конденсатора и двигателя составили 7,79 и 1,76 %. Им соответствуют дозы ψ_μh = 0,171 << 1 и ψ_μl = 0,044 << 1.

Таким образом, вместо неуниверсальной системы параметров ЭМС, основанной на понятии гармоник, в стандарте достаточно нормировать только дозы несинусоидальности. Эти параметры не могут охватывать все виды электрооборудования, компьютеры, системы питания и др. Поэтому в соответствующих стандартах на ЭМС возможно использование других стандартных электроприемников. Не исключено нормирование не структуры и параметров ВФ, а предельных переходных или частотных функций – как в [9].

Расчет параметров ЭМС. В задаче первого типа исходными данными для расчетов являются графики помех или их характеристики. Наличие моделей ЭМС позволяет применить известные методы теории автоматического управления.

Для исследования процессов на выходе ВФ удобно использовать метод парциальных реакций [10], который заключается в представлении ВФ в виде параллельно включенных инерционных звеньев первого порядка. Сумма парциальных реакций i(t) каждого звена на помеху дает искомый процесс на выходе ВФ.

Количество инерционных звеньев равно количеству полюсов знаменателя передаточной функции. Для передаточной функции (16) полюса

где . Инерционные звенья имеют сопрягающие частоты γ_1,2 = – s_1,2 и коэффициенты передачи

               (18)

Передаточная функция раскладывается на простые множители, поэтому разности s − s_1,2 в числителе и знаменателе сокращаются, и деление 0/0 не происходит. То обстоятельство, что параметры инерционных звеньев являются комплексными величинами, не препятствует расчетам, так как в конечном результате мнимые величины уничтожаются. Для принятого стандартного конденсатора получим: ά = 12741 с^–1, λ = 78611 с^–1, ά_1,2 = 1,013 × 10^–8 ± j128,35.

Если в качестве входного блока используется линейный фильтр, то метод парциальных реакций применяется к линейной системе с передаточной функцией, равной произведению передаточных функций блока 1 и ВФ. Количество полюсов знаменателя при этом возрастает.

В случаях, когда помеха задана спектральной плотностью, а для оценки ЭМС достаточно знать дисперсию реакции, вместо метода парциальных реакций можно использовать частотные методы, определяя АЧФ по передаточной функции ВФ.

В задаче второго типа дозы могут быть получены либо расчетным путем, как в задаче первого типа, либо измерены специализированным прибором. Измерители доз должны иметь структурную схему и параметры, совпадающие с моделями ЭМС стандартных электроприемников. Использование одной и той же модели ЭМС позволяет избежать расхождения в результатах, полученных расчетным путем или измерениями.

Приложение.Рассмотрим простой метод «эквивалентной синусоиды», основанный на том, что за время t_f стандарт σ искаженного напряжения мало отличается от действующего значения U_f синусоиды. Действительно, при нулевом среднем значении помехи между ними существует соотношение

где K_U – коэффициент искажения синусоидальности в %. В [2] допускаются искажения величиной 5 и 8 % – для сетей 6-20 и 0,38 кВ. В этом случае амплитуды будут разниться всего на 0,125 и 0,319 %.

В качестве амплитуды синусоиды принимается величина

Для графика на рис. 1,а

где корреляционный момент определяется формулой (5).

Как и следовало ожидать, найденная амплитуда практически не отличается от вычисленной по B_fФ: при θ_* = 0,0018 всего на 0,19 %. Малое расхождение в помехах, выделенных поциклично по формулам коэффициентов Фурье и методом эквивалентной синусоиды, позволяет в последнем случае пренебречь корреляцией между синусоидой и помехой.

Выводы. 1. Физический смысл, достоверность и универсальность оценок ЭМС обеспечивается путем моделирования воздействий несинусоидальности напряжения на электрооборудование: дополнительных потерь мощности, максимального перегрева и теплового износа изоляции. Модель ЭМС целесообразно принимать в виде взвешивающего фильтра и энергетического блока.

2. В задачах, требующих учета ущерба от несинусоидальности напряжения рекомендуется использовать модели ЭМС конкретного электрооборудования и сети, а для целей нормирования – модели ЭМС «стандартных» электродвигателя и конденсатора, которые позволяют ввести универсальные показатели: низко- и высокочастотную дозы несинусоидальности напряжения.

3. Применение метода парциальных реакций для определения характеристик процесса на выходе взвешивающего фильтра модели ЭМС позволяет получать аналитически точное решение, унифицирует и упрощает расчеты.

СПИСОК ЛИТЕРАТУРЫ

1. Куренный Э.Г., Ковальчук В.М., Коломытцев А.Д. Оценка качества электроэнергии с использованием моделей объектов. – В кн.: Качество электроэнергии в сетях пром. предприятий. Материалы конференции. – М.: МДНТП, 1977.
2. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
3. CEI/IEC 61000-4-15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.
4. Куренный Э.Г., Дмитриева Е.Н., Куренный Д., Цыганкова Н.В. Совершенствование модели фликера. – Электричество, 2003, № 2.
5. Mirra C., Sani G. Il fenomeno del flicker. Analizi delle sue caracteristiche. Techniche di misura e metodi di limitazione. – L’Elettrotecnica. – 1987.
6. Малафеев С.И. О динамических и энергетических характеристиках силовых конденсаторов. – В сб. научных трудов: Оптимизация системы питания и электрооборудования электротехнологических установок. – К: Ин-т электродинамики АН УССР, 1989.
7. ГОСТ 1282-88. Конденсаторы для повышения коэффициента мощности. Общие технические условия. Группа Е.53. – Введ. 01.01.89.
8. Лютий О.П. Оцінка електромагнітної сумісності за несинусоїдальності напруги в електричних мережах з швидкозмінним навантаженням. – Праці Інституту електродинаміки Національної академії наук України, № 1 (1), Київ, 2002. – С. 109-115.
9. ГОСТ 19705-89. Системы электроснабжения самолетов и вертолетов. Общие требования. Нормы качества электроэнергии. Введ. 01.01.90.
10. Kourennyi E.G., Petrosov V.A., Chernikova L.V. Linear filtration on random processes in EMC models: the “partial reaction” method. – Fifteenth International Wroclaw symposium and exhibition: Electromagnetic compatibility 2000. – Wroclaw: National Institute of Telecommunications, 2000, part II.
11. Гутников В.С. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990.
12. Теория автоматического управления / Под ред. А.А. Воронова. – М.: Высшая школа, 1977, ч. 1.