Источник: Материалы ХІ Международной научно-технической конференции «Автоматизация технологических объектов и процессов. Поиск молодых» 17-20 мая 2011 года. — Донецк, ДонНТУ — 2011, с. 150–152.

Коливання струму навантаження здійснює низькочастотну модуляцію миттєвих значень и напруги, що приводить до появи в процесі u(t) інтергармонік. Ця обставина не враховується в стандарті [1], де нормуються лише канонічні вищі гармоніки. При цьому для визначення гармонік рекомендується використовувати прямокутне вікно шириною k = 0,32 с або вікно Хемінга.
Метою роботи є оцінювання похибок, що виникають при розрахунках гармонік за стандартною процедурою, на прикладі гармонічних коливань напруги. Всі параметри режиму вважаються незмінними, рівними номінальним значенням 1 і f = 50 Гц.
Миттєві значення напруги при гармонічних коливаннях частотою l у Гц і розмахом dU у в.о. описуються формулами [2]

(1)

де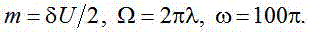
Як видно, тут окрім несучої частоти 50 Гц є інтергармоніки з кутовими частотами w ± W, яким відповідають частоти

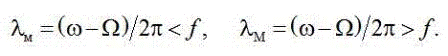
Якщо частоти є раціональними числами, процес (1) буде періодичним з тривалістю циклу Тm, яка залежить від співвідношення між частотами інтергармонік і 50 Гц. Величина Тm звичайно не співпадає з 0,32 с – вона може бути меншою або більшою за ширину вікна. Наприклад, при l = 10 Гц маємо Тm = 0,1 с, а при 12 Гц – 0,5 с.
Покажемо, що при Тm ¹ 0,32 с розкладання в ряд Фур’є на інтервалах k дає спектр квазігармонік (термін з [3]), суттєво відрізняється від фактичного. Позначимо: t1 і t2 – початок і кінець інтервалу 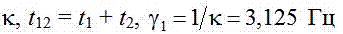і

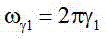– частота і кутова частота першої квазігармоніки, р – порядок квазігармоніки, img226 За відомими формулами на інтервалі t2 – t1 = k отримаємо коефіцієнти ряду Фур’є при р ¹ 0 і u ¹ 0:

Якщо u = 0, то відповідні члени з добутками синусів дорівнюють нулю, а з добутками косинуса на синус – величині k/2 = 0,16c При р = 0 постійний член дорівнює b0/2. Амплітуди гармонік

(2)

Згідно з [1] враховуються гармоніки з амплітудами не меншими за 0,001. Оскільки відношення 0,032/0,02 є цілим числом, гармоніка 50 Гц, коли р = 16, визначається точно. Інші гармоніки (2) суттєво відрізняються від фактичних: з’являються постійні складові, канонічні гармоніки і квазігармоніки, які не існують. Спектр гармонік змінюється від вікна до вікна, хоча він є постійним.
Проаналізуємо, як похибки у визначенні спектру позначаються на оцінках впливу несинусоїдальності на електроприймачі. Для короткості розглянемо ідеальні активний опір, індуктивність і ємність, ЕМС яких оцінюється за ефективним значенням 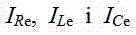несинусоїдальних складових відповідних струмів.
У в.о. струм і напруга на активному опорі співпадають. Інтергармоніки процесу (1) мають однакове діюче значення img230 тому незалежно від їх частоти точна величина

Для визначення струмів через індуктивність (ємність) амплітуди гармонік потрібно розділити (помножити) на відносні значення частот img232 і img233 Тоді

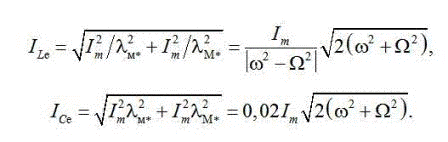
При обробці на інтервалі (t1,t2) ефективні значення визначаються виразами:

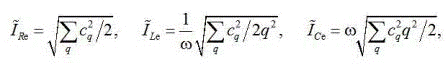
де підсумовування виконується від 0 до порядку останньої гармоніки, яка враховується (для ємності – від q = 1)
Різниця між цими і точними значеннями наочно видна для індуктивності: поява в спектрі постійної складової, якої у дійсності немає, дає нескінченний струм на усіх інтервалах по 0,32 с.
У діючих мережах коливання є випадковими, для яких поняття гармоніки не існує. Тому обробка по вікнах буде давати ще більші похибки для активного опору і ємності. Для індуктивності постійні складові також будуть давати нескінчений струм.
Таким чином, обробка осцилограм напруги за стандартною процедурою не дозволяє достовірно оцінювати вплив несинусоїдальності напруги на електроприймачі, що підтверджує висновок з [3] щодо заміни в [1] показників ЕМС за «гармоніками» на дози несинусоїдальності.

Перелік посилань
ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.
Бессонов Л.А. Теоретические основы электротехники / Л.А. Бессонов. – М.: Высшая школа, 1964.
Куренный Э.Г. Оценка несинусоидальности напряжения при анализе качества электроэнергии / Э.Г. Куренный, А.П. Лютый // Электричество, 2005, № 8.

Наверх