УДК 621.311.153.2

Источник: Наукові праці Донецького національного технічного університету. Серія: «Електротехніка і енергетика», випуск 10 (180). – Донецьк: ДонНТУ, 2011. - С. 48-52.

The task of instantaneous voltage values imitation is considered at the set voltage fluctuations. In general case it is offered to design an electro-receiver by changing conductivities. For designing the method of imitation by voltage sine semiwaves is developed.

Постановка задачі. У деяких задачах електромагнітної сумісності (ЕМС) для забезпечення достовірності потрібно розглядати процес u(t) зміни за часом миттєвих значень напруги (криву напруги): наприклад, при оцінюванні несинусоїдальності від коливань напруги. В стандарті рекомендується лише приблизне рішення крива напруги приймається у вигляді кусково-лінійної функції. До того ж при цьому існує невизначеність у виборі виду апроксимації: на рис. Б.1,а  з цього стандарту ординати з’єднані похилими прямими, а на тому ж рис. Б.1,б  – вертикальними стрибками. Це веде до похибок в імітації миттєвих значень і, як наслідок, в оцінках показників ЕМС.

             Усунення невизначеності є метою статті. Розглядаються два типа вихідного завдання. У загальному випадку відомими вважаються процеси зміни g(t) активної і b(t) реактивної провідностей джерела коливання, а для проектування – розрахункові коливання  напруги. Як звичайно, вважається, що напруга Uж центра живлення не містить завад ЕМС. Напруга вимірюється у відносних одиницях щодо номінального значення Uн.

             Загальний випадок. Спокійне навантаження задається постійними провідностями gп і bп. Джерело коливань має постійні gпк, bпк і змінні gпк(t), bпк(t) складові провідностей. Сумарним провідностям

                                                    (1)

відповідають опір і індуктивність

                                                                                  (2)

 

де w50 = 100p,  – квадрат повної провідності. Слід відзначити, що на відміну від динамічних провідностей вирази (1) по суті дають тренди статичних провідностей, які визначаються по діючих значеннях струмів і напруг.

У проектуванні відомими є активні і реактивні складові струмів навантаження, по яких розраховуються провідності – шляхом помноження на  Якщо задаються струм  і  то при

            

            

 

             Розрахункова схема містить у собі активний опір rм і індуктивність Lм мережі, з якими послідовно з’єднані r(t) і L(t). Сумарні параметри схеми  і  є функціями часу. Синусоїдальна напруга має фазу y. При такій схемі лінійне диференціальне рівняння для миттєвих значень і струму має змінні коефіцієнти:

 

                                                                                                                   (3)

 

Позначивши через  

запишемо відомий загальний розв’язок у вигляді

 

                                                                                                                                       (4)

 

де  а  Найбільше значення початкового струму дорівнює ІМ при

             У розрахунках доцільно приймати найбільшу величину початкового струму, яка дорівнює ІМ при  В проектуванні використовують періодичні функції параметрів режиму. У цьому випадку, без розрахунку перехідного процесу, визначається періодичній розв’язок [3].

             Напруга на шинах

 

                                                                                                                                                               (5)

 

є результатом низькочастотної модуляції несучої синусоїди 50 Гц внаслідок зміни провідності.

В [1] діючі значення U напруги визначаються шляхом осереднення квадрата (5) на послідовних інтервалах q = 0,01 с. Оскільки напруга u(t) є безперервним процесом, потрібно виконувати не таке дискретне, але й безперервне осереднення

 

                                                                                                                                                                      (6)

 

Тренд напруги визначається середньоквадратичним осередненням процесу (6) на інтервалі 60 с  [1]:

 

                                                                                                                                                                 (7)

 

             Коливання напруги у відносних одиницях становлять

 

                                                                                                                                                                    (8)

 

а при розрахунку доз флікеру напруги вираз (8) потрібно помножити на 100 %.

             Як приклад, розглянемо випадок, коли коливання створюються електроприймачем, який працює у режимі «увімкнено-вимкнено» з постійним опором. Позначимо:  Струм розраховується послідовно для всіх ділянок часу. На першій ділянці тривалістю tу струм, як відомо, дається виразом

 

                                                                                                                 (9)

 

             Початкове значення струму дорівнює нулю, а кінцеве  є початковим для другої ділянки – паузи. Тут напруга відсутня, тому, строго кажучи, потрібно було б моделювати процеси звільнення енергії через дугу при вимкненні. Для практики можна вважати, що перехідний процес проходить з тією ж сталою часу. Тоді

 

            

 

             Напруга на шинах визначається за виразом (5): на першій ділянці

 

                                                                                        (10)

 

де  і враховано, що  На другій ділянці

 

            

             Якщо заданим є початкове значення u1(0), то потрібно визначити відповідний кут y0 – дорівнюванням виразу (10) до цього значення. Наприклад, коли u1(0) = 0, то

 

                                                                                                                                             (11)

 

             Суттєво, що у перехідному періоді процес (10) є несинусоїдальним і неперіодичним, а тому не може бути представленим рядом Фур’є – він має безперервний спектр.

             Інтегрування згідно з (6) виконується у кінцевому вигляді, але вираз для U(t) є громіздким і тут не приводиться.

Імітація півхвилями синусоїд. У проектуванні за графіком струму розраховуються втрати  напруги з середнім значенням  Як на рис. А.1 з [1], тренд вважається незмінним: V = 1, тому коливання напруги й напруга на шинах становлять

Це означає, що вісь часу графіка коливань напруги співпадає з горизонталлю одиниця на графіку напруги. Оскільки флікермодель не пропускає постійної складової, при V = 1 паралельний перенос осі часу не впливає на результат розрахунку доз флікеру.

Згідно з [1] процес  являє собою ґратчасту функцію з кроком q, тому на кожному інтервалі q процес  можна приблизно представити півхвилями синусоїд. Їх вершини розташовуються посередині інтервалів з абсцисами  де k = 1, 2, … – номер інтервалу. Для цих моментів часу діючі значення півхвиль повинні співпадати з  тому на k-му інтервалі ординати півхвиль за абсолютним значенням будуть у  разів більшими, що для k-го інтервалу дає

 

                                                                                                                      (12)

 

Цей процес, як і (5), є безперервним, але на межах інтервалів похідні будь-якого порядку змінюються стрибком – при нерівності абсолютних значень вершин сумісних інтервалів. Окрім того, за винятком прямокутних коливань, півхвилі синусоїд виходять за межі огинаючих процесу (5). Тому перетворення (6) дає процес  який не співпадає ані з  ані з  – за винятком моментів часу te. З ТОЕ відомо, що вираз (12) лише приблизно описує низькочастотну модуляцію. Похибка буде тим більшою, чим ближче частота модуляції до 50 Гц. Похибка залежить від виду й характеристик процесів, тому у кожному конкретному випадку потрібно перевіряти можливість використання (12) замість (5).

Періодичні коливання. Застосування методу півхвиль спочатку розглянемо на прикладі меандру (рис. 1,а) та гармонічного коливання (рис. 1,б) з розмахом dU і частотою l = 25 Гц, коли у періоді  с розташовується ціле число s = 2 циклів t50 = 0,02 с  синусоїди 50 Гц. При одиночному тренді напруга на шинах періодично змінюється від  до

У випадку меандру в циклі tl буде дві півхвилі з амплітудою  і дві – з  Інтегрування згідно з (6) при w100 = 200p дає безперервну функцію

 

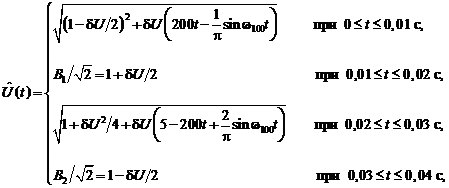                                                          (13)

 

де множники 100 і 200 мають розмірність 1/с. Її графік показано на рис. 1,а  потовщеною лінією. Розмах коливань залишився без зміни, але коливання суттєво відрізняються від ідеалізованого прямокутника (пунктир): сумарна довжина горизонтальних ділянок зменшилася на 2q (з 0,04 до 0,02 с), а стрибки відсутні. Це приводить до зменшення доз флікеру напруги.

Рисунок 1 – Імітація прямокутних і гармонічних коливань з частотами: а, б – 25 Гц; в, г – 100/3 Гц

 

Розглянутий приклад показує, що відтворити прямокутні коливання неможливо – лише при малих частотах, менших за 5 Гц, похибка не буде великою.

Перейдемо до випадку, коли цикл коливання не є кратним 0,02 с, що не дозволяє виконати імітацію точно за цикл tl. Подолання цієї принципової труднощі можна здійснити двома способами: округлити тривалість циклу в меншу і більшу сторони до кратних 0,02 с значень tl1 і tl2 або збільшити тривалість циклу до величини Тl, більшу за tl.

За першим способом розглядаються два коливання з частотами  і  а результати розрахунку доз потім інтерполюються. Чим менше відрізняються l1 і l2 від l, тим менше похибка. Однак при великих частотах розкиди l1,2 – l збільшуються. Наприклад, при l = 3 Гц, коли tl = 0,333 с  округлювання дає цикли 0,32 і 0,34 с, яким відповідають частоти l1 = 3,125 і l2 = 2,941 Гц з розкидами 0,125 і –0,059 Гц. При частоті ж 32 Гц з циклом 0,031 с  маємо цикли 0,03 і 0,04 с, частоти 33,333 і 25 Гц, розкиди вже дорівнюють 1,333 і –7 Гц. Для верхньої межі 35 Гц частотного діапазону коливань застосування способу неможливе, оскільки округлення циклу tl = 0,0286 с  у меншу сторону до 0,02 с  дає частоту 50 Гц, коливання з якою не існують.

З цієї причини потрібно виконувати імітацію для трьох-чотирьох частот, менших за ту, що розглядається, а результати розрахунку доз екстраполювати.

За другим способом частота і цикл коливань не змінюються, а тривалість Тl визначається за умови, що при цілому числі s цілою буде й величина 0,02sl. Так, при частоті 100/3 Гц умова 2s/3 виконується при s = 3, що дає Тl =3×0,02 с. Якщо частота є цілим числом, то тривалість циклу не перевищує 1 с. Коли ж частота виражається ірраціональним числом (наприклад, l = p  Гц), то Тl ® ¥, тобто процес  буде неперіодичним.

Коли стрибки на графіку коливань попадають на моменти часу, які не є кратними q (на рис. 1,в при 0,015 і 0,045 с), то виникає невизначеність з амплітудою півхвилі. Щоб уникнути стрибків на графіку  приймемо за амплітуду ординату, яка відповідає середині стрибка (на рис. 1,в будуть амплітуди  При частоті 100/3 Гц графік  (потовщена лінія) вже не має горизонтальних ділянок з ординатами  що ще більше зменшує дозу.

Для ідеалізованого гармонічного коливання вираз для  є єдиним, але громіздким. В нього входять частоти 100 Гц, l, 2l, 2(50 – l), 100 – l і 100 + l. Це свідчить про те, що точно відтворити гармонічні коливання неможливо. В окремих випадках деякі частоти зникають при інтегруванні. Так, при частоті 25 Гц відсутня частота 100 Гц. На рис. 1,б,г потовщеними лініями показано графіки цих функцій, які також відрізняються від заданих (пунктир), проте у меншій мірі.

             Приклад. Побутовий електроприймач напругою 220 В, потужністю Рн = 1 кВт і cos j = 0,8 працює у режимі «робота-пауза» з періодом, значно більшим за 1 с – час перехідного процесу у флікермоделі. Мережа має активний 0,74 і індуктивний хм = 0,56 Ом опори. Для оцінювання ЕМС за дозою флікеру при  розрахувати напругу на електроприймачі точним і наближеним методами.

             У випадку, що розглядається, для моментів стрибків провідності початкові умови є нульовими, тому достатньо імітувати процес u(t) тільки для одного стрибка. За час роботи параметри розрахункової схеми є незмінними:  Ом, rS = 49,14 Ом,  Ом,  Гн, z = 60,5 Ом, хS = 36,86 Ом, LS = 0,1173 Гн, zS = 61,428 Ом. Відповідно gп = 425,3 с–1, ІМ = 5,065 А, jS = 0,6435 рад, e(t) = exp{–425,3t}, j = 0,6435 рад, rп = 0,7222 Ом.

             Для можливості зіставлення з методом півхвиль, приймемо, що и1(0) = 0. Тоді згідно з (11) y0 = 0,007194 рад, а формула (10) дає

 

            

 

             По цьому процесі визначимо функцію (6), яка плавно змінюється від 1 до значення  (рис. 2, крива 1), тобто розмах коливань становить 0,015. В проектуванні на ділянці уві-

мкнення втрата напруги розраховується по номінальному струмові  за наближеною формулою

 

 

яка дає значення  менше за 0,985. Розрахунковий графік (пунктир) принципово відрізняється від фактичного, оскільки при t = 0 напруга змінюється стрибком.

За методом півхвиль достатньо розглянути проміжок часу від 0 до 0,01 с. Інтегрування згідно з (6) дає процес

 

 

Рисунок 2

графік якого представлено на рис. 2 кривою 2. Границі, до яких прямують криві, відрізняються менше ніж на 1 %, але крива 2 згасає не точно за 0,01 с, а теоретично – у нескінченності. Практично рівня 5 % від  крива 2 досягає за 0,0126 с, тобто на 26 % більше за 0,01 с.

Висновки. 1. Імітування кривих напруги потрібно виконувати з використанням моделювання джерела коливань змінними параметрами: активним опором й індуктивністю.

2. Для орієнтовного оцінювання параметрів ЕМС криву напруги можна імітувати послідовністю півхвиль синусоїд на інтервалах 0,01 с, амплітуди яких визначаються заданими графіками коливань напруги.

Література

1. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. в Украине с 01.01.2000.

2. Дмитриева Е.Н. Совершенствование цифровой фликер-модели для оценки колебаний напряжения / Е.Н. Дмитриева, В.А. Топчий // Электричество, 2010, № 7. – С. 20-25.

3. Курінний Е.Г. Доза флікеру при періодичних коливаннях напруги / Е.Г. Курінний, О.М. Дмитрієва, В.О. Топчій // Праці Інституту електродинаміки Нац. академії наук України, 2009, вип. 22. – С. 123-129.

4. CEI/IEC 61000-4-15. Electromagnetic compatibility – Part 4, Section 15: Flickermeter – Functional and design specification. 1997.

 

Рекомендовано до публікації проф., д.т.н. Заболотним І.П.

Наверх