Источник: Журнал «Электричество», 2010 г., №7.
Предлагается тренд и колебания напряжения разделить по частотному принципу. Разработаны рекомендации по совершенствованию входного блока и взвешивающего фильтра цифровой фликер-модели.
Ключевые слова: электромагнитная совместимость, фликер-модель, тренд напряжения, колебания напряжения, фильтрация колебаний
При любых способах измерения и расчета однозначность оценок электромагнитной совместимости (ЭМС) по дозе фликера напряжения обеспечивается, если определяемые показатели ЭМС не допускают разной трактовки. Действующие нормы этому очевидному требованию не удовлетворяют. Во-первых, используются два разных определения колебаний. В самом деле, согласно [1] из процесса изменения во времени напряжения U(t) выделяют участки единичных изменений, измеряя размахи колебаний в процентах номинального напряжения. Напротив, во входном блоке фликер-модели IЕС [2, 3] выделяются «приведенные колебания» напряжения (КНП – термин наш), равные отношению разности между напряжением и усредненным напряжением к усредненному напряжению. Во-вторых, в [1, п. Б.2.1] действующее значение напряжения определяется путем квадратичного усреднения мгновенных значений за полпериода основной частоты, а в [2, 3] – путем квадратичного детектирования. В-третьих, в [2, 3] колебания приводятся к номинальному напряжению лампы, что предполагает контроль напряжения на зажимах ламп. Согласно же [1] ЭМС контролируется в точке общего присоединения (общей точке). Выраженные в процентах усредненные напряжения в этих точках не совпадают, что создает принципиальные трудности в выборе коэффициента приведения в общей точке.
Первоначально структурная схема фликер-модели была ориентирована на аналоговую реализацию фликерметра. При этом потребовалось принять сравнительно небольшую ширину θ=1 мин и усредняющего окна Дирихле (кратко – окна), а также ввести фильтры ФВЧ высших и ФНЧ низших частот с частотами среза 0,05 и 35 Гц. Копировать такую структурную схему в цифровой модели нецелесообразно.
В статье предложены пути устранения отмеченных неопределенностей, а также рекомендации по усовершенствованию цифровой фликер-модели. Изложение ведется на примере модели со стандартной лампой накаливания 60 Вт, 230 В [2, 3], но все выводы относятся и к более корректным моделям: с расширенным частотным диапазоном, с лампами другого вида и мощности [4].
Исходные положения. В соответствии с существующей практикой раздельного нормирования помех ЭМС из процесса U(t) будем выделять колебания напряжения.
Колебания напряжения вызывают дополнительное утомление человека, а также влияют на силовые электроприемники, устройства управления и др. Механизмы и последствия воздействия колебаний на эти объекты разные, поэтому для их оценки должны создаваться соответствующие динамические модели ЭМС, объединять которые с фликер-моделью представляется нецелесообразным.
Воздействие на объекты любой помехи ЭМС определяется всем ее графиком, поэтому с принципиальной точки зрения следует рассматривать непрерывные графики колебаний напряжения без искусственного их разделения на отдельные участки по тому или иному признаку.
Зрительная система человека реагирует на изменение яркости. При большой освещенности скачкообразное изменение яркости от J до J ± ΔJ не изменяет порог восприятия ΔJ / J. Это означает, что восприятие зрительной системой изменений яркости зависит от тренда. Одни и те же колебания вызывают меньший или больший фликер при усредненном напряжении, большем или меньшем номинального, что необходимо учитывать при оценивании фликера.
Колебания представляют собой результат низкочастотной модуляции несущего сигнала 50 Гц. При малых частотах колебаний (λ << 50 Гц) модуляция в пределах каждого полупериода несущественно изменяет синусоидальную форму сигнала, поэтому два способа определения действующих значений напряжения (детектирование и усреднение) дают близкие результаты. Однако при частотах колебаний 6 Гц и более искажение формы происходит все в большей мере, что приводит к разным результатам. При случайных колебаниях, а также при наличии несинусоидальности различия будут еще большими. Далее, как и в [1], для получения действующих значений (не тренда!) принято среднеквадратичное усреднение на интервалах 0,01 с.
Частотные диапазоны. В [6] под трендом V(t) понимается любая составляющая процесса, период которой превышает «длину» реализации. Это означает, что ширина окна должна быть не менее половины длительности записи. В [1-3] кратковременные дозы фликера Рstопределяются за десятиминутные промежутки времени. Следовательно, ширина окна должна превышать 5 мин, а используемые в [1, 2] одноминутные усредненные значения не могут рассматриваться как тренд. Это было бы корректным при длительности записи 2 мин, однако уменьшать длительность записи до 2 мин нельзя, так как утомление человека от фликера начинает проявляться через 8 – 10 мин.
Определение тренда становится корректным только после выбора физически обоснованной ширины окна. В рассматриваемой задаче для этого необходимо исходить из амплитудно-частотной функции (АЧФ) взвешивающего фильтра (ВФ) фликер-модели IЕС.
Исходя из казалось бы интуитивно ясного представления о том, что колебания есть быстрые изменения напряжения, ранее (например в ГОСТ 13109–87) в качестве определяющего признака использовалась средняя скорость изменения напряжения. В этом случае тренд трактовался бы как медленная компонента напряжения. Однако при таком подходе график напряжения искусственно разбивается на участки с большой и малой скоростями, что противоречит принципу непрерывности воздействий.
В соответствии с теорией фильтрации (например [7]) тренд и колебания напряжения будем разделять по частотному признаку. Теоретически эта задача неразрешима, так как у случайных процессов спектральная плотность определена в бесконечном диапазоне от 0 до ∞. Такой же диапазон будут иметь и тренд, и колебания, а потому их диапазоны полностью перекрываются. Для практических целей надо установить правую граничную частоту λVmахтренда и левую λKmin колебаний. Очевидно, что при этом должно выполняться условие λVmах ≤ λKmin.
На рис. 1 представлена АЧФ А4(λ) (1) взвешивающего фильтра без ФВЧ и ФНЧ. В этом случае реакция ВФ на колебания напряжения описывается дифференциальным уравнением 4-го порядка. Фильтры повышают порядок уравнения n до 11, сжимая АЧФ А11(λ) ВФ в областях низших и высших частот. На рис. 1 эта АЧФ не показана, так как она мало отличается от кривой 1.
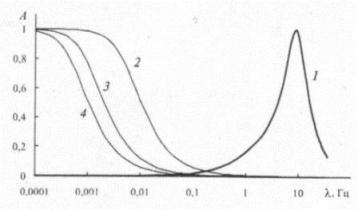
Рис. 1. Амплитудно-частотные функции: 1 – ВФ фликер-модели; 2, 3 и 4 – окон Дирихле шириной 1, 5 и 10 мин
Граничная частота определяется по АЧФ. Для этого необходимо задать малое граничное значение Атin, которое должно быть меньше допустимой погрешности определения доз фликера 0,05 [1]. Это условие определено тем, что АЧФ относится к гармоническим колебаниям, а при колебаниях другого вида погрешность может быть большей. Расчеты показывают, что при n=4 в области значений Атin от 0,01 до 0,05 существует линейная зависимость:

Для определенности примем Атin=0,01. В этом случае граничная частота равна 0,0524 Гц.
Перейдем к определению граничной частоты тренда. В существующих стандартах на интервале θ усредняется квадрат напряжения. Как показано в приложении, при оценивании фликера целесообразно перейти к более простому усреднению самого процесса U(t), что позволяет определять граничную частоту по АЧФ окна.
В темпе реального времени усреднение (символ Мθ) осуществляется по прошлому процесса в пределах отt –θ доt. В этом случае выделенный тренд (знак ~):
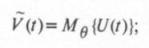
АЧФ окна:
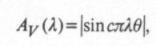
где 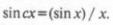
Тренд отстает от процесса U(t) на время θ/2.
Недостатком АЧФ (3) является наличие боковых лепестков, которые могут быть подавлены более сложными окнами [7]. Однако преимуществом окна Дирихле, предопределяющим его широкое применение, является простота реализации. Ось частот на графиках АЧФ обычно дается в логарифмическом масштабе. При этом боковые лепестки затемняют рисунки, поэтому для наглядности АЧФ окна будем условно представлять АЧФ инерционного звена как

с постоянной времени T= θ / 2,25 мин, близкой к огибающей АЧФ окна [8, рис. 2.5]. Однако все дальнейшие расчеты выполняются по фактической АЧФ (3).
Подстановка в (3) Атiпдает трансцендентное уравнение для аθ =0,01, где множитель 60 определяет размерность ширины окна в секундах. Решив уравнение методом подбора и выполнив аппроксимацию, получим аθ =0,236 Атiп-1,06. Отсюда найдем соотношение между граничной частотой и шириной окна:
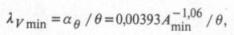
где θ измеряется в минутах; при Атin=0,01 граничная частота равна 0,519/ θ.
Для окон шириной 1, 5 и 10 мин получим значения 0,519; 0,104 и 0,052 Гц. Сравнивая их с граничной частотой 0,0524 Гц диапазона колебаний, заключаем, что тренд и колебания будут практически разделены лишь при θ =10 мин.
Следует отметить, что в [1, рис. 1] принят частотный диапазон от 0,1 до 1620 мин-1, т.е. от 0,00083 до 13,5 Гц. Хотя это согласуется с идеей расширения частотного диапазона [4], но формально противоречит требованиям [2, 3]. Поскольку п. 5.3 из [1] относится к зрительным работам, на сегодня рис. 1 и табл. В.1 этого стандарта необходимо привести в соответствие с табл. 2 из [2, 3]. При этом любая точка на кривой размахов колебаний должна давать одно и то же допустимое значение дозы фликера.
Понятие колебания. Существующее определение колебания через единичные изменения напряжения не отвечает требованию непрерывности воздействий. Действительно, даже в частных случаях, когда интервалы времени Δti между единичными воздействиями превышают время затухания tз переходной функции ВФ фликер-модели, исключать из рассмотрения участки Δti нельзя (в [1] Δti ≥ 1 с). Хотя в этих случаях реакция ВФ может рассматриваться отдельно для каждого единичного изменения в пределах tз, но оставшиеся нулевые паузы с длительностью Δti – tз необходимо учитывать при построении функции кумулятивных вероятностей. В [1] такой подход показан в приложении В путем введения приближенных коэффициентов – и то лишь для ограниченного числа форм единичных изменений частотой λ менее 1 Гц. В результате стремление к упрощению, наоборот, привело к усложнению практических расчетов, так как формализовать выделение единичных изменений в расчетах на компьютере не так просто, а главное – не нужно.
Понятие колебания не может быть абсолютным, а приобретает определенность только после выбора усредняющего окна. В этом случае под колебанием напряжения естественно понимать разность между напряжением и трендом:
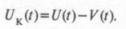
Обозначим через UПприведенное к тренду напряжение (в процентах):
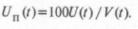
На вход фликер-модели подается КНП:

Принятое в [2, 3] квадратичное детектирование было вынужденным решением для аналоговой фликер-модели. В цифровом варианте действующие значения напряжения целесообразно определять так же, как и в [1]: путем квадратичного усреднения на интервале 0,01 с. При этом не только достигается единообразие, что очень важно для директивных документов, но и существенно упрощается структура входного блока – достаточно лишь реализовать преобразование (8).
При контроле ЭМС на зажимах ламп понятие КНП является физически обоснованным и однозначным. Иначе обстоит дело с контролем в общей точке. Из-за наличия потерь напряжения и регуляторов напряжения между напряжениями в конкретной сети освещения и в общей точке нет однозначной связи, поэтому обосновать значение коэффициента приведения в общей точке не представляется возможным – решение может быть принято лишь путем экспертных оценок. Учитывая очевидную условность показателей ЭМС в общей точке, можно вообще отказаться от умножения на коэффициент приведения.
Погрешности фильтрации. Оценить погрешности фильтрации тренда возможно, если только он известен из физических соображений. Например, если нагрузка создающего колебания напряжения электроприемника является эргодическим процессом, то тренд будет неизменным, определяемым средним значением нагрузки, которая теоретически вычисляется за бесконечный промежуток времени. Поэтому усреднение на любом конечном интервале дает погрешность. Проиллюстрируем это на примере графика напряжения (рис. 2, кривая 7) с неизменным трендом V0 (горизонталь 2) и гармоническим колебанием с амплитудой В, равной половине размаха δUt. Длительность цикла tλ =1/λ.
Подставив сумму этих компонент в (2) и выполнив интегрирование, получим

Здесь второе слагаемое дает абсолютную погрешность, которая представляет собой синусоиду с той же частотой λ, но с амплитудой

и запаздыванием во времени θ /2 (кривая 3 на рис.2). При принятом в [1] дискретном усреднении на смежных интервалах график тренда 4 является ступенчатым.

Рис. 2. К фильтрации тренда и колебаний напряжения
Выделенный тренд отличается от фактического качественно и количественно: он изменяется во времени и имеет меньшую амплитуду (за исключением случаев, когда sinπλθ=0). Это объясняется тем, что усредняющее окно частично воспринимает колебание как тренд.
Относительная погрешность (в процентах)
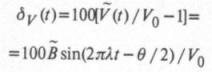
имеет абсолютное максимальное значение
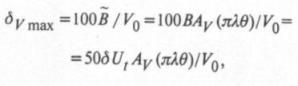
пропорциональное АЧФ окна. При очень малых частотах, когда АЧФ близка к единице, погрешность достигает значения 50δUt/V0. На границе диапазона при Атin=0,05 она не превышает 2,50δUt/V0, а при 0,01 – 0,5δUt/V0. Если колебания отсутствуют (В=0), погрешность равна нулю.
Вследствие неточности фильтрации тренда выделенное КНП
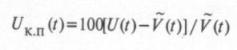
отличается от (8).
Для рассматриваемого графика напряжения после подстановки (9) и (12) получим

где

Из-за знаменателя в (13) КНП не является синусоидой, но так как В= V0, то приближенно получим синусоиду
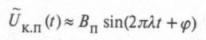
c амплитудой и фазой:
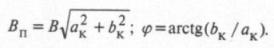
На рис. 2,б при V0=Uнфактическое колебание представлено кривой 5, а рассчитанное по формуле (9) – кривой 6. Разность между кривой 1 и ступенчатым трендом 4 дает «колебания» 7.
При гармонических колебаниях доза фликера пропорциональна размаху колебаний

и не зависит от фазы. Поэтому относительная погрешность определения дозы фликера при той или иной частоте равна погрешности определения амплитуды:

Эта погрешность не должна превышать допустимое значение 5% определения дозы фликера. Из-за наличия боковых лепестков в АЧФ окна зависимость погрешности от частоты имеет колебательный характер (рис. 3,а). Ее экстремумы по абсолютному значению убывают с увеличением частоты колебаний. При частотах более 0,0464 Гц погрешности не превышают значение 5%.
Найдем диапазон частот, в котором можно рассчитывать дозу фликера без учета фильтров. В этом случае погрешность оценки ЭМС
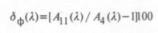
достигает больших значений в зоне малых и больших частот (рис. 3,5). Диапазон частот от 0,178 до 28,9 Гц, в котором погрешность не превышает 5%, перекрывает диапазон частот от 0,5 до 25 Гц из [2, 3, табл.1], что свидетельствует о возможности отказа от ФВЧ и ФНЧ.
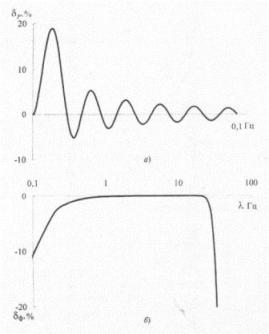
Рис. 3. Погрешности определения доз фликера при гармонических колебаниях напряжения: а - при фильтрации одноминутного тренда; б - при отказе от ФВЧ и ФНЧ.
Выражение (18) оценивает погрешности при гармонических колебаниях. При колебаниях в форме меандра погрешности будут больше.
Совершенствование фликер-модели. До внесения в [2, 3] изменений по расширению частотного диапазона и учета фактических условий освещения должна использоваться существующая фликер-модель. Рассмотрим возможность ее улучшения в предположении, что физически обоснованной является АЧФ А4(λ) без фильтров.
При одноминутном усреднении отсутствие требований к полосе пропускания создает неопределенность в разграничении тренда и колебаний напряжения и в выборе структуры входного блока фликер-модели. В самом деле, если принять Атin > 0,03 то можно отказаться от ФВЧ, а при Атin < 0,03 – нельзя.
Кроме того, имеется некоторое несоответствие между понятием тренда, связанным с длительностью измерений, и шириной окна: кратковременная доза измеряется на интервалах 10 мин против 1 мин. Это усложняет структуру входного блока, так как требуется регистрация текущих одноминутных значений – хотя бы с шагом 1 мин.
На наш взгляд, исходя из определения тренда, ширину окна следует принимать равной длительности измерения, т.е. 10 мин. Во-первых, при этом погрешность выделения тренда практически будет отсутствовать. Во-вторых, ФВЧ становится излишним. В-третьих, поскольку отсчет тренда достаточно проводить один раз: в конце десятиминутного интервала измерения, коэффициент 230/V будет учитываться после расчета десятиминутной дозы. Это обстоятельство позволяет отказаться и от входного блока, в котором осуществляется приведение к опорному напряжению.
Исключение фильтров понижает порядок д.у. с 11 до 4, что упрощает и ускоряет расчет реакций ВФ. Возможные же погрешности, обусловленные дискретным представлением процесса U(t) с шагом 0,01 с, подавляются самим ВФ, поскольку на частотах 1/0,01 = 100 Гц и более амплитуда АЧФ А4(λ) очень мала и не превышает 0,0185.
Приложение. Покажем, что при оценивании колебаний напряжения вместо среднеквадратического усреднения можно использовать усреднение на интервале действующих значений напряжения.
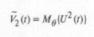
При θ=0 процессы (П-1) и (2) совпадают между собой и с U(t). Наибольшее расхождение между ними будет при θ→∞, когда процесс (П-1) вырождается в горизонталь с ординатами, равными эффективному значению напряжения Uэ, а (2) – среднему значению Uс. Поэтому предельная погрешность усреднения (2) по абсолютному значению составляет
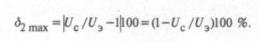
Рассмотрим колебания напряжения в форме меандра, которые дают наибольшие дозы фликера по сравнению с периодическими колебаниями любой другой формы. Так как тренд не изменяется, то для этого случая
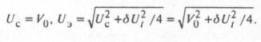
Согласно (П-2)

отсюда при допустимой погрешности найдем
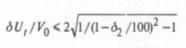
– условие возможности использования (2) вместо (П-1). Если допускается погрешность в 1%, то отношение размаха колебаний к тренду не должно превышать 0,285, а при 5% - уже 0,657. Встречающиеся в практике колебания намного меньше предельных значений, поэтому целесообразно использовать более простое преобразование (2), что делает задачу оценивания ЭМС линейной сразу на начальном этапе, существенно упрощая выкладки. Например, если процесс U(t) является случайным, с нормальным распределением ординат, то при усреднении U(t) и тренд будет нормальным случайным процессом, числовые характеристики которого определяются по среднему значению корреляционной функции напряжения. Без затруднений, с применением метода парциальных реакций [9], определяются и характеристики реакции ВФ, которая также имеет нормальное распределение. При среднеквадратичном же усреднении отсутствует даже приближенное решение.
Выводы. 1. Вместо одноминутного среднеквадратичного усреднения, принятого в [1 – 3], под трендом целесообразно понимать среднее (не эффективное!) значение процесса изменения напряжения за время измерения кратковременных доз фликера 10 мин. Колебания напряжения следует определять как отнесенную к тренду разность между напряжением и трендом, исключив понятие «единичных изменений».
2. Кривые допустимых размахов периодических колебаний для ламп должны соответствовать допустимым дозам фликера во всем диапазоне частот, в связи с чем табл. В. 1 из [1] и табл. 2 в [2, 3] должны совпадать.
3. При измерении и расчете доз фликера целесообразно исходить из цифровой, а не аналоговой фликер-модели, что позволяет существенно упростить контроль ЭМС: во входном блоке вычисляются только действующие значения напряжения и десяти минутные средние значения; исключаются фильтры высших и низших частот; средние значения учитываются после вычисления доз фликера.
СПИСОК ЛИТЕРАТУРЫ
1. ГОСТ 13109-97. Межгосударственный стандарт. Электрическая энергия. Совместимость технических средств электромагнитная. Нормы качества электрической энергии в системах электроснабжения общего назначения. – Введ. с 01.01.1999.
2. ГОСТ Р 51317.4.15-99 (МЭК 61000-4-15-97). Совместимость технических средств электромагнитная. Фликерметр. Технические требования и методы испытаний.
3. IЕС 61000-4-15. Electromagnetic compability. Part 4. – Section 15: Flickermetr – Functional and design specification, 1997.
4. Куренный Э.Г., Дмитриева Е.Н., Куренный Д., Цыганкова Н.В. Совершенствование модели фликера. – Электричество, 2003, № 2.
5. Watson J. F. Power supply to critical loads. Part 2. – Power Engineering , December 1966.
6. Бендат Дж., Пирсол А. Измерение и анализ случайных процессов. – М.: Мир, 1974.
7. Гутннков В.И. Фильтрация измерительных сигналов. – Л.: Энергоатомиздат, 1990.
8. Шидловский А.К., Вагин Г.Я., Куренный Э.Г. Расчет электрических нагрузок систем электроснабжения промышленных предприятий. – М.: Энергоатом издат, 1992.
9. Куренный Э.Г., Лютый А.П., Черникова Л.В. Метод парциальных реакций для анализа процессов на выходе линейных фильтров в моделях электромагнитной совместимости. – Электричество, 2006, № Ю.