Источник: Журнал «Электричество», 2009 г., №3.
Предложен новый подход к определению коэффициента искажения синусоидальности напряжения в сетях с дуговыми сталеплавильными печами. На базе экспериментальных исследований на машиностроительном предприятии доказано преимущество новой методики по сравнению с существующей как по точности, так и по степени сложности расчетов. Приводится пример расчета.
Ключевые слова: электрические сети, напряжение, качество, искажение синусоидальности, дуговые сталеплавильные печи, расчет
Экспериментальные исследования, проведенные авторами, показали, что уровни высших гармоник в напряжении электрической сети, питающей дуговые сталеплавильные печи (ДСП), далеко выходят за пределы, допустимые ГОСТ 13109-97. Кроме того, они существенно превышают те значения, которые получаются расчетным путем при использовании существующей методики [2]. Повышенный уровень гармоник часто приводит к выходу из строя конденсаторов в компенсирующих устройствах, установленных на подстанции. Подобных нежелательных явлений можно избежать, если еще на стадии проектирования правильно рассчитать коэффициент искажения синусоидальности напряжения КUи заложить в проект необходимые мероприятия по его снижению. Наиболее объективные результаты дает вероятностный подход к расчету коэффициента КU, который является функцией случайного тока нагрузки ДСП.
Перед составлением вероятностной модели для расчета КUрассмотрим исходные положения, используемые в традиционной методике расчета искажений напряжения в сетях с ДСП [1].
Коэффициент искажения синусоидальности напряжения определяется формулой:
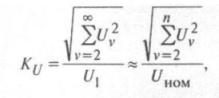
где Uν– действующее значение фазного напряжения ν-й гармоники; U1–действующее значение фазного напряжения основной частоты, которое обычно заменяется его номинальным значением Uном; п – номер последней из учитываемых гармоник.
Расчет коэффициента искажения синусоидальности напряжения по ГОСТ 13109-97 ограничивается 40-й гармоникой (n=40), а предлагаемая методика расчета, как показано далее, учитывает весь гармонический ряд, позволяя тем самым повысить точность расчета.
В [1] при расчете коэффициента КUпредлагается использовать правую часть формулы (1), ограничиваясь при этом 7-й гармоникой (п = 7). Искомую п-ю гармонику рекомендуется находить из эмпирического соотношения:

где I – ток печного трансформатора в расчетном режиме.
Для определения максимальных значений гармоник тока предлагается брать в расчет номинальный ток печного трансформатора, что, как показано далее, не совсем верно. Вторую гармонику принимают равной току третьей гармоники (I2 = I3). Для группы одновременно работающих ДСП в режиме расплавления металла ток I по (2) умножается на соответствующий коэффициент, зависящий от того, одинаковые ДСП или нет. Фазное напряжение n-й гармоники в расчетной точке питающей сети
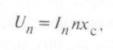
где хс — индуктивное сопротивление питающей сети от расчетной точки до условной точки бесконечной мощности.
Подкоренное выражение в формуле (1) с учетом соотношений (2) и (3) можно переписать следующим образом:
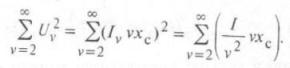
С учетом того, что I2 = I3, правую часть уравнения перепишем в виде:
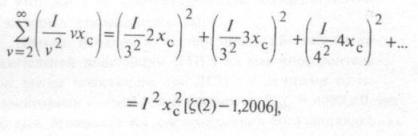
где  – дзета-функция Римана [3|:
– дзета-функция Римана [3|:
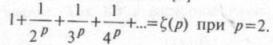
Тогда с достаточно высокой точностью
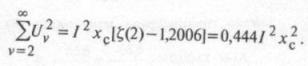
После подстановки правой части выражения (6) в формулу (1) получим:
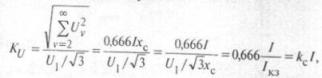
где Iкз — ток короткого замыкания в расчетной точке сети; kс— коэффициент, который в дальнейшем условимся называть коэффициентом схемы электроснабжения в расчетной точке, А-1.
Для удобства коэффициент схемы измеряется в %/А. тогда

Таким образом, коэффициент искажения синусоидальности напряжения является линейной функцией случайною аргумента I:
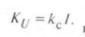
Пусть известны параметры распределения тока нагрузки ДСП I: М[I] – математическое ожидание тока: D[I] – дисперсия тока, тогда, применяя к (9) теоремы о числовых характеристиках [3], найдем параметры распределения величины КU:


где М[КU] и D[КU]– математическое ожидание и дисперсия КU соответственно.
Среднее квадратическое отклонение КU:

так как коэффициент схемы kсможет быть только положительным. В (12) σ[I]– среднее квадратическое отклонение тока печной нагрузки.
Будем считать, что ток печной нагрузки в режиме расплавления металла подчиняется нормальному закону. Такое утверждение согласуется с результатами экспериментальных исследований, проведенных авторами. Следовательно, величина КUтоже будет подчиняться нормальному закону.
Согласно указаниям [4] максимальные значения токов эксплуатационных коротких замыканий (КЗ) не должны превышать 3,5Iмом (Iном – номинальный ток печного трансформатора). При этом ограничение тока производят поднятием электродов. В случае отказа регулятора мощности и задержке по этой причине подъема электрода печной выключатель отключается с выдержкой времени. Уставка срабатывания выключателя составляет 3÷4 Iном. Для доказательства справедливости данного утверждения на рис. 1 приведен фрагмент графика тока нагрузки одной дуговой печи ДСП-5, работающей в режиме расплавления металла. Штриховой линией отмечен уровень тока, соответствующий значению 3,5 Iном. Как видно из рис. 1, ток дуговой нагрузки нередко превышает уровень, указанный в ПУЭ.

Рис. 1. Фрагмент графика тока нагрузки дуговой сталеплавильной печи в режиме расплавления металла
Максимальное значение коэффициента искажения синусоидальности напряжения, обусловленное работой одной ДСП, равно:

т.е. по этой формуле можно определить максимальное значение коэффициента искажения синусоидальности напряжения еще на стадии проектирования системы электроснабжения.
Из (13) можно найти параметры распределения случайной величины КU. Для этого воспользуемся «правилом трех сигма» [3]:
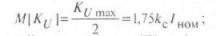
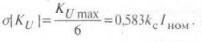
Если в режиме расплавления металла работает группа ДСП, то полученные результаты необходимо умножить на соответствующие коэффициенты, о которых упоминалось выше.
Пример. К одной из секций шин 6 кВ главной понизительной подстанции (ГПП) на машиностроительном заводе подключено три ДСП-5 с печными трансформаторами номинальной мощности Sном = 4000 кВА каждый. Мощность КЗ для этой секции шин составляет 5КЗ = 165 МВ-А.
Требуется дать вероятностную оценку изменения коэффициента искажения синусоидальности напряжения на данной секции шин ГПП.
Решение. Ток КЗ в расчётной точке:

По (8) определяем коэффициент схемы:
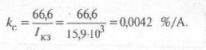
Номинальный ток печного трансформатора:

Для трех ДСП

Параметры распределения случайной величины КUсогласно (14) и (15) будут следующими:

Подставив найденные параметры в формулу плотности вероятности нормального закона, получим:
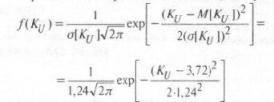

По этому выражению рассчитана и построена на рис. 2 кривая распределения коэффициента искажения синусоидальности напряжения 1.
При экспериментальных исследованиях использовались серийно выпускаемые цифровые портативные приборы. В частности, гистограмма и параметры распределения величины КUполучены с помощью анализатора гармоник и прибора дня измерения статистических характеристик.
Гистограмма 2 коэффициента КUсоответствует периоду времени непрерывной работы печей, равному 9 ч (с 15.00 до 24.00). При этом в расчет принимались только те участки времени, когда все три печи одновременно работали в режиме расплавления металла. Эксперимснтальные значения параметров распределения: М[КU] = 3,72%, σ[КU] = 1,34%.

Рис. 2. Значения коэффициента искажения синусоидальности напряжения в режиме расплавления метала: 1 – по предлагаемой методике; 2 –из эксперимента; 3 – по существующей методике
При сравнении теоретических и экспериментальных параметров распределения, а также графиков рис. 2 можно сделать вывод, что они хорошо согласуются друг с другом. Некоторая положительная асимметрия экспериментального распределения объясняется, скорее всего, инерционностью регуляторов мощности, а также наличием выдержки времени при отключении печных выключателей.
Расчёт КUпо существующей методике [1] даёт значение 1,78% (на рис. 2 – штриховая линия 3).
Выводы. 1. Предложенная методика позволяет определить ожидаемое значение коэффициента искажения синусоидальности напряжения КUв cетях с ДСП на стадии проектирования системы электроснабжения.
2. При расчете ожидаемого значения коэффициента искажения синусоидальности напряжения в сетях ДСП целесообразно:
использовать вероятностный подход, взяв за основу нормальный закон распределения тока дуговой нагрузки;
параметры распределения тока дуговой нагрузки выбирать исходя из указаний ПУЭ, а именно: максимальное значение тока ДСП должно быть равным не менее 3,5Iиом. а не номинальному значению, как это принято в [2];
учитывать всю гамму высших гармоник без ограничения, используя при этом дзета-функцию Римана при р = 2.
3. Результаты, полученные с применением предложенной методики расчёта, дают хорошее совпадение с экспериментальными данными.
СПИСОК ЛИТЕРАТУРЫ_
1. Иванов В.С., Соколов В.И. Режимы потребления и качество электроэнергии систем электроснабжения промышленных предприятий. – М.: Энергоатомиздат, 1987.
2. Двайт Г.Б. Таблицы интегралов и другие математические формулы: Учебное ПОС. 9-е изд. – С. Петербург: Лань, 2005.
4. Вентцель Е.С. Теория вероятностей. –М.: Высшая школа, 2001.
5. Правила устройства электроустановок. Раздел 7, глава 7.5 «Электротермические установки». Приказ Минэнерго России
от 08.07. 2002 № 204.