Ідентифікація моменту інерції електроприводу рекурентним методом найменших квадратів

Журов І.О., Толочко О.І.
ДВНЗ «Донецький національний технічний університет»

Источник: Вісник кафедри «Електротехніка» за підсумками наукової діяльності студентів. - Донецьк, ДонНТУ, 2011 – С.22-24.

          Для якісного керування електромеханічною системою необхідно мати максимум достовірної інформації про об'єкт керування. Ця задача ускладнюється у випадку, коли параметри ОК невідомі чи змінюються в процесі його роботи. Наприклад, в електроп-риводі з асинхронним двигуном такими параметрами є активні опори обмоток статора й ротора, взаємна індуктивність, момент інерції приводу, який володіє найбільшим діапазоном змін у процесі роботи.
          Мета роботи. Розробка алгоритму ідентифікації моменту інерції електроприводу з використанням рекурентного методу найменших квадратів (РМНК) та аналіз його роботи на математичній моделі системи векторного керування асинхронним двигуном з короткозамкненим ротором.
          Вираз для вектору оцінок параметрів об’єкту керування за РМНК має вигляд [1]:

                                                                                                                                           (1)

де 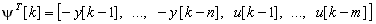– вектор виміряних сигналів на k-му такті; 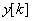– вихідний сигнал об’єкту керування на k-му такті; 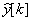– вихідний сигнал адаптивної моделі на k-му такті;
          Вихідний сигнал адаптивної моделі є добутком вектору виміряних сигналів та вектору оцінок параметрів . При цьому в загальному випадку частина коефіцієнтів можуть бути відомими величинами. Тоді вектор повинен містити тільки невідомі коефіцієнти, вектор – тільки ті компоненти вхідних та вихідних сигналів, які помножуються на невідомі коефіцієнти, а сума добутків решти компонент на відомі коефіцієнти додається у вигляді відомого сигналу :

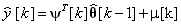                                                                                                                                                            (2)

          Вектор корекції 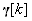розраховується за наступним виразом:

                                                                                                                                                         (3)

де 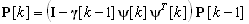– матриця, яка впливає на швидкість ідентифікації, для якої задається початкова умова 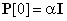; - велика константа; 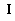- діагона-льна одинична матриця.
          Відмітимо, що у випадку, коли ідентифікації підлягає лише один параметр, всі вище розглянуті векторні величини стають скалярними.
          Для розробки алгоритму ідентифікації моменту інерції зручно використати передатну функцію механічної частини приводу:

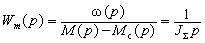                                                                                                                                                      (4)

де 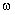– кутова швидкість обертання ротора; 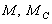– електромагнітний момент двигуна та момент статичного опору, приведений до валу двигуна, відповідно.
          При дискретизації ПФ (4) методом Тастіна отримуємо наступне різницеве рівняння, яке є початковим для побудови адаптивної моделі:

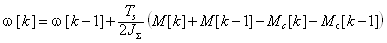                                                                                                       (5)

де 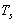– період дискретності адаптивної моделі.
          З аналізу рівняння (5) витікає, що задача ідентифікації моменту інерції приводу пов’язана з задачею визначення моменту статичного опору, величина якого не піддається прямому вимірюванню. Тому, для ідентифікації 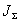бажано мати математичну модель, яка не містила б моменту статичного опору. Вирішення цієї проблеми розглянуто у [2].
          Остаточний вираз для дискретної моделі механічної частини електроприводу:

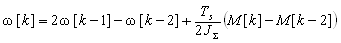                                                                                                                  (6)

          З урахуванням (6) рівняння (1) приймає вигляд:

                                            (7)

          Ідентифікований параметр формується з параметрів адаптивної моделі згідно рівнянню:

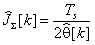                                                                                                                                                                                (8)

та фільтрується аперіодичною ланкою з постійною часу Tf = 1мс. Початкові умови ідентифікаторів вибрані наступними: .
          Структурна схема ідентифікатора, розроблена у пакеті Matlab додатку Simulink представлена на рис. 1.

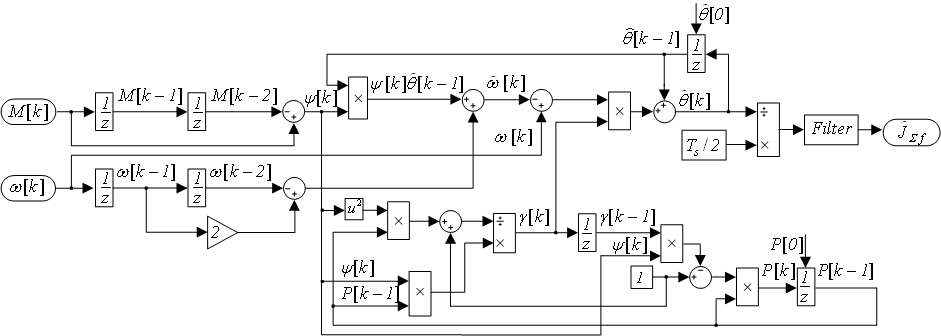Рисунок 1 – Структура ідентифікатора моменту інерції електроприводу

          Результати моделювання системи векторного керування АД з ідентифікацією приведені на рис. 2.

Рисунок 2 – Перехідні процеси з урахуванням ідентифікації моменту інерції електроприводу

          Аналізуючи отримані результати, можна зробити висновок, що на швидкість ідентифікації впливає константа, закладена в ідентифікаторі в якості початкової умови.
          Точність ідентифікації залежить від періоду дискретності ідентифікатора. При цьому необхідно, щоб період дискретності ідентифікатора був рівний або менше у ціле число разів періоду дискретності регулятора струму.
          Розроблений алгоритм ідентифікації дає адекватний результат як при постійному моменту інерції електроприводу, так і у разі його зміни у процесі роботи.

Література

1. Изерман Р. Цифровые системы управления / Изерман Р. – М.: Мир, 1984. – 541 с.
2. Трандафілов В.М. Особливості градієнтного метода ідентифікації моменту інерції електроприводу / В.М. Трандафілов, О.І. Толочко, В.В. Божко // Автоматизація технологічних об’єктів та процесів. Пошук молодих. Збірник наукових праць X Міжна-родної науково-технічної конференції аспірантів та студентів в м. Донецьку 18-20 тра-вня 2010 р. – Донецьк: ДонНТУ, 2010. – С. 260-262.