Параметричний астатизм в системі модального керування двомасовим електромеханічним об‘єктом

Журов І.О., Толочко О.І.
ДВНЗ «Донецький національний технічний університет»

Источник: Електротехнічні і електромеханічні системи: Матеріали XVI Всеукраїнської студентської науково-технічної конференції, м. Севастополь, 18-20 квітня 2011 р. - Севастополь: Вид-во СевНТУ, 2011. - С. .

          Одним із засобів боротьби з пружними коливаннями в двомасових елект-ромеханічних системах є вживання принципів модального керування [1].
          Синтез систем модального управління (СМУ) виконується з умов забезпечення бажаного розподілення їх полюсів. Внаслідок цього забезпечується бажана поведінка основної регульованої координати при відпрацюванні керуючої дії. Але поведінка інших координат при відпрацюванні керуючої дії та усіх координат (у тому числі і основної регульованої) при накиді навантаження може бути якою завгодно.
          Одним з параметрів СМУ, що суттєво впливають на її статичні та динаміч-ні властивості, є середньогеометрічний корінь (СГК) характеристичного полінома (ХП). Наприклад, від цього параметра у СМУ залежить величина статизму привода за швидкістю двигуна та виконавчого органа механізму при накиді навантаження. У [1] показано, що при деяких параметрах ДЕМО система з регулятором стану повного порядку може мати не тільки від’ємну, але й нульову або навіть додатну статичні похибки за швидкістю у названому вище режимі.
          Можливість зробити систему астатичною за навантаженням без включення в регулятор інтегральної складової є досить привабливою.
          Але для розв‘язання цієї задачі треба знайти аналітичний вираз для розрахунку параметрів СМУ, які забезпечують параметричний астатизм.
          Для цього в роботі здійснено синтез СМУ, знайдено її передавальну функцію за збуренням і вираз для статичної просадки швидкості двигуна і механізму при накиді навантаження. Прирівнявши отриманий вираз до нуля, одержано формулу для розрахунку середньогеометричного кореня характеристичного полінома СМУ 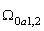, що забезпечує параметричний астатизм:
          
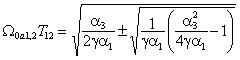
          В наведеній формулі 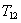– стала часу пружних коливань двомасового об‘єкта, 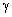– коефіцієнт розподілення мас, 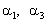– коефіцієнти характеристичного полінома при відповідних степенях оператора Лапласа, унормовані за середньо-геометричним коренем.

Література

1. Борцов Ю.А. Автоматизированный электропривод с упругими связями / Борцов Ю.А., Соколовский Г.Г. – СПб.: Энергоатомиздат, 1992. – 288 с.