Особливості градієнтного метода ідентифікації моменту інерції електроприводу

Трандафілов В.М., Толочко О.І., Божко В.В.
ДВНЗ «Донецький національний технічний університет»

Источник: Автоматизація технологічних об’єктів та процесів. Пошук молодих. Збірник наукових праць X Міжнародної науково-технічної конференції аспірантів та студентів в м. Донецьку 18-20 травня 2010 р. – Донецьк, 2010. – С. 260-262.

          Переважна більшість механізмів мають постійний момент інерції. Однак існує категорія робочих машин, в яких момент інерції є функцією кута повороту (кривошипно-шатунні, мальтійські, ексцентрикові та інші механізми) чи змінюється в залежності від навантаження та інших факторів (підйомно-транспортні, тягові механізми, моталки, роботи-маніпулятори та інші). Системи керування такими механізмами, зазвичай, будуються за принципом підпорядкованого керування. Помилково розраховане значення або зміна моменту інерції в процесі роботи системи електроприводу призводить до погіршання якості перехідних процесів в такій системі. Наприклад, у випадку зменшення моменту інерції підвищується коливальність перехідних процесів, а при збільшенні цього параметру перехідні процеси уповільнюються. Надзвичайно чутливими до зміни моменту інерції є спостерігачі стану, що відновлюють момент статичного опору на валу двигуна, інформація про який може використовуватися для комбінованого керування за збуренням, для запобігання виникнення пробуксовок, вирівнювання навантажень в багатодвигунних електроприводах, при формуванні діаграм відпрацювання заданих переміщень, оптимальних за тепловими втратами, тощо. Невірне значення моменту інерції в моделі об‘єкта регулювання призводить до помилкової роботи спостерігача на ділянках розгону та гальмування [1]. Тому питання ідентифікації моменту інерції в процесі роботи і адаптації системи до його зміни є актуальними. Розглянемо можливість ідентифікації моменту інерції ненормованим градієнтним методом, який відрізняється своєю простотою. Згідно з цим методом процес ідентифікації описується системою рівнянь [2]:

          

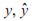де – вектор параметрів адаптивної моделі; u – вектор вхідних сигналів; – вихідний сигнал досліджуваного об’єкта та адаптивної моделі відповідно; F – коефіцієнт адаптації; n – номер кроку.
          Дискретна модель механічної частини одномасової системи електроприводу на n- та (n-1)-ому кроці при чисельному інтегруванні (ЧІ) методом прямокутників – Forward Euler (FE):

          
          

де Ts – період дискретності; J – момент інерції електроприводу; 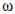– кутова швидкість ротора; M – електромагнітний момент двигуна; M_c – момент статичного опору. Знаходимо різницю між рівнянням (2) та (3) з припущенням, що за один крок ЧІ момент статичного опору залишається незмінним, тобто M_c[i-1]=M_c[i], де і = 0, 1, 2, …. Після перетворень маємо:

          
       Відповідно до системи рівнянь (1) приймемо наступні позначення в рівнянні (4): .
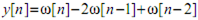          При дискретизації моделі механічної частини приводу можуть бути використані також такі методи ЧІ як модифікований метод прямокутників – Backward Euler (BE) та метод трапецій – Trapezoidal (TR), для яких можна здійснити перетворення, аналогічні (2)-(4).
          Для аналізу роботи ненормованого градієнтного методу ідентифікації була використана система векторного керування синхронним двигуном з постійними магнітами, розроблена в пакеті Matlab. Результати моделювання (при Ts=20 мкс та F=0,05) зображені на рис. 1-2. На них продемонстровано процес ідентифікації моменту інерції при застосуванні різних алгоритмів ЧІ в моделі об‘єкта регулювання в режимі роботи за трапецеїдальною тахограмою з накидом навантаження на ділянці розгону та скиданням навантаження на ділянці гальмування.

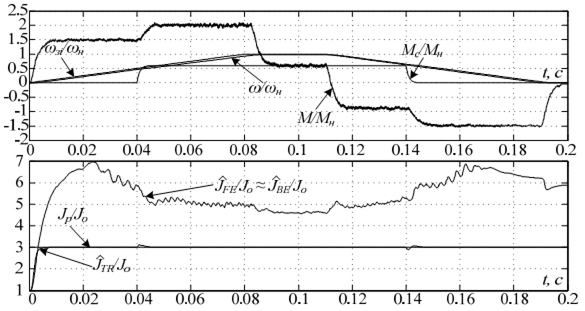Рисунок 1 – Перехідні процеси при Jо=Jр/3

          На рис. 1-2 прийняті наступні позначення: 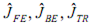– момент інерції, ідентифіковані при використанні методу чисельного інтегрування FE, BE та TR відповідно; Jo – момент інерції, на який налаштована система і який є початковим для адаптивної моделі; Jр – реальний момент інерції; 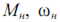– номінальний момент та номінальна кутова швидкість двигуна; – завдання на кутову швидкість від задавача інтенсивності.

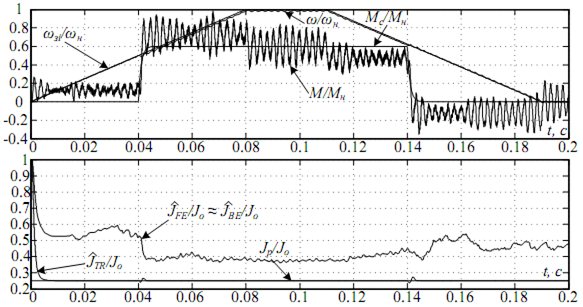Рисунок 2 – Перехідні процеси при Jo=4Jр

          З аналізу перехідних процесів випливає, що при використанні ЧІ методом трапецій момент інерції відновлюється на порядок точніше, ніж при використанні методів прямокутників.
          До напрямків подальших досліджень можна віднести аналіз роботи інших модифікацій градієнтного методу (наприклад, нормованого та покращеного), аналіз впливу періоду дискретності та коефіцієнта адаптації на процес ідентифікації, порівняння градієнтних методів з іншими методами параметричної ідентифікації.

          Перелік посилань

1. Методика настройки наблюдателя состояния, восстанавливающего статический и динамический моменты двигателя постоянного тока / О.И. Толочко, П.Х. Коцегуб, П.И. Розкаряка, Г.С. Чекавский // Сборник научных трудов ДГТУ. – Днепродзержинск, 2007. – С. 434-436.
2. Ljung L. System Identification - Theory For the User, 2nd ed / Lennart Ljung – PTR Prentice Hall, Upper Saddle River, N.J., 1999. – 609 pp.