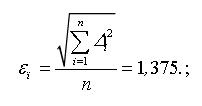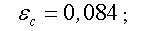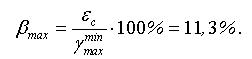Моделирование процесса торможения многоканатной шахтной подъемной установки со шкивом трения, оборудованной дисковым тормозом
М.А. Рутковский
Источник: http://www.nbuv.gov.ua/.../Rutkovskiy.pdf
Состояние вопроса
Подъемные машины являются важнейшими технологическими объектами
угольных и рудных шахт. С ростом производительности горных предприятий и глубины разрабатываемых месторождений увеличивается масса поднимаемых грузов и растет коэффициент массивности подъемных установок. Эти факторы приводят к повыше
нию требований, предъявляемых к тормозным сис
темам подъемных машин. Применяемые в настоящее
время на подъемных машинах тормозные системы
радиального типа настраиваются на создание опреде
ленного тормозного усилия, независимого от вели
чины и знака концевой нагрузки, и в ряде случаев
оказываются не в состоянии обеспечить интервал ве
личин замедлений предохранительного торможения в
пределах, нормируемых Правилами безопасности.
На смену традиционно выпускаемым подъемным
машинам с радиальными тормозными устройствами,
зарубежными машиностроительными компаниями
(ABB, ASEA, GHH, SIEMAG и др.) освоен выпуск и
производство подъемных машин с дисковыми тормо
зами, имеющими, по сравнению с радиальными, ряд
преимуществ: малую величину холостого хода, рав
номерное распределение давления на тормозную ко
лодку, отсутствие силовой рычажной системы, ком
пактность и малую металлоемкость.
Использование дисковых тормозов позволяет осу
ществлять ступенчатое приложение тормозного уси
лия по определенному алгоритму, что обеспечивает
гибкую настройку тормоза под конкретную подъем
ную установку. Таким образом, техническое совер
шенствование подъемных установок, идущее по пути
снижения их металлоемкости и повышения произво
дительности, управляемости и безопасности, не воз
можно без замены радиальных тормозных систем на
дисковые. Применение дисковых тормозных уст
ройств существенно повышает технический уровень
машин, делает их более конкурентоспособными и яв
ляется объективным результатом развития современ
ных подъемных машин.
Однако отечественная промышленность пока не
выпускает подъемные машины, оборудованные дис
ковыми тормозами, что в первую очередь связано с
недостаточной изученностью процесса торможения
подъемной установки при использовании многомо
дульных дисковых тормозов. Для обоснованного вы
бора параметров дисковых тормозных устройств, ра
ботающих в сложной динамической системе подъем
ной установки, необходимо провести исследования
динамических явлений, протекающих во взаимосвя
занных элементах: подъемных канатах, тормозной
системе, упругих звеньях машины.
Разработкой конструкции и определением рацио
нальных параметров дисковых тормозных устройств
занимались Белобров В.И., Степанов А.Г., Траубе Е.С.
Но выбор параметров дисковых тормозов проводился
без учета динамических явлений в подъемных канатах
и без проверки соблюдения требований Правил безо
пасности по величинам допустимых ускорений.
Димашко А.Д. [1] выбор параметров тормозной
системы многоканатной подъемной установки про
изводил на основе моделирования подъемной уста
новки как абсолютно твердого тела, при этом преду
сматривая следующие допущения:
– тормозной момент имеет постоянную величину,
неизменную во времени;
– не учитывается влияние колебательных процес-
сов в подвесных канатах на уменьшение силы сцеп-
ления их со шкивом трения;
– не учитывается время холостого хода тормозно-
го устройства.
В реальных подъемных установках величина тор-
мозного момента переменна во времени, колебатель-
ные процессы в подвесных канатах влияют на усилия
прижатия их к поверхности шкивов трения, поэтому
неучет этих факторов приводит к ошибкам при опре-
делении параметров дисковой тормозной системы.
Одной из последних работ по исследованию много-
модульных дисковых тормозов является работа Трибу-
хина В.А. [2]. Им было предложено ввести в математи-
ческую модель подъемной установки нулевую массу,
соединяющую ветви в нижней части многоканатной
подъемной установки, однако, данное допущение при-
водит к возможности передачи усилий между ветвями
через петлю канатов, что неверно. Кроме того, при ана-
лизе динамики подъемной установки в режиме тормо-
жения не учитывалось влияние демпфирующих свойств
каната, не был проведен анализ отсутствия проскальзы-
вания каната по шкиву трения.
Таким образом, обоснование параметров дисковых
тормозных устройств на основе исследования процес-
са торможения многоканатной шахтной подъемной
установки является актуальной научной задачей.
Цель работы
Разработать рекомендации по вы-
бору параметров дисковых тормозных устройств для
многоканатной шахтной подъемной установки со
шкивом трения.
Основная часть
В соответствии с работой [3],
одномерная континуальная система многоканатной
подъемной установки со шкивами трения может быть
заменена дискретным динамическим аналогом, со-
стоящим из небольшого количества масс, соединен-
ных между собой невесомыми пружинами и демпфе-
рами. Используя данную методику, расчетная схема
шахтной подъемной установки может быть представ-
лена в следующем виде (рис. 1).
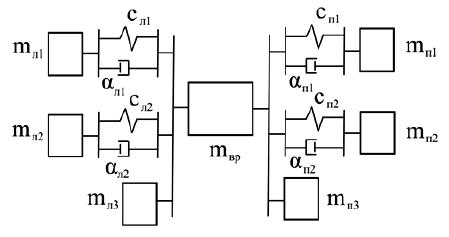
Рис. 1. Расчетная схема динамического аналога подъ
емной установки: mвр – масса вращающихся час
тей подъемной машины; mл1, mл2, – массы осцил
ляторов левой ветви; сл1, сл2 – коэффициенты
жесткости осцилляторов левой ветви; л1, aл1 – коэффициенты демпфирования осцилляторов ле
вой ветви; mл3 – жесткая масса левой ветви; mп1,
mп2, mп3, сл1, сл2, aл1, aл1 – соответствующие параметры правой ветви.
Массы осцилляторов определяются по формулам:
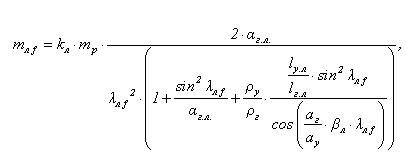
(1)

(2)
где mр = mс + mгр – расчетная масса, равная массе
подъемного сосуда и наибольшей массе поднимаемого груза; kл, kп – безразмерные параметры, характеризующие отношения масс концевых грузов соответственно левой и правой ветвей к массе расчетного груза; aг, aу – скорости пробега волны упругой деформации соответственно в головном и уравновешивающем канатах; pг, pу – погонные массы соответственно головного и уравновешивающего канатов; y.л l, y.п l – длина уравновешивающего каната для левой и правой ветви; г.л l , г.п l – длина головного каната для левой и правой ветви; л f y , п f y – собственные числа частот колебаний левой и правой ветвей, которые
определяются при решении трансцендентных уравнений графическим методом [3]
Для пятимассовой системы, представленной на
рисунке 1, процесс торможения подъемной
установки описывается следующей системой
дифференциальных уравнений:
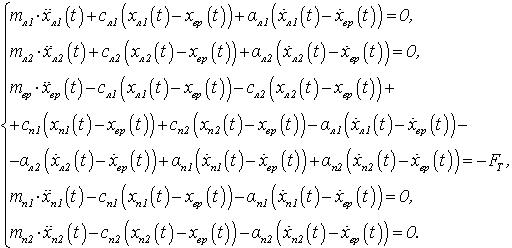
(3)
где FT – усилие, развиваемое тормозом, которое определяется выражением:

(4)
Начальные условия
Система дифференциальных уравнений (6) реше
на в MathCad с использованием функции rkfixed, реа
лизующей метод Рунге-Кутта четвертого порядка с
постоянным шагом интегрирования
Z = rkfixed (x,L1,L2,m,D), (5)
где x – вектор начальных условий; L1 – начало ин
тервала интегрирования; L2 – конец интервала интег
рирования; m – число шагов интегрирования; D –
вектор производных в явном виде.
Зависимость тормозного усилия от времени тор
можения была принята соответствующей рис. 2 для
рассматриваемой подъемной машины МПМН 6,3*2.
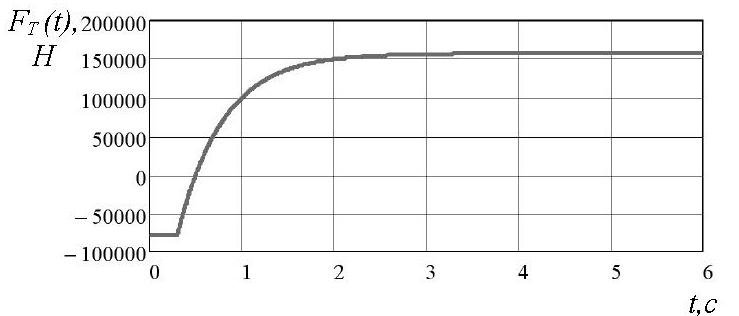
Рис. 2. Характеристика тормозного усилия
Вектор производных в явном виде

(6)
В результате решения была получена матрица Zi,j,
состоящая из 10 столбцов. В первом столбце содер
жатся значения текущего времени t, а в остальных
находятся значения функций смещений и скоростей
масс, входящих в систему дифференциальных урав-
нений.
Используя найденные значения смещений и ско
ростей, были рассчитаны усилия в пружинах осцил
ляторов по формулам:

(7)
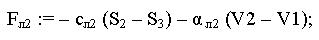
(8)
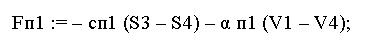
(9)

(10)
Уравнения (1–10) представляют собой математическую модель динамического аналога многоканатной подъемной установки.
Для тестирования этой модели сравним результа
ты вычислений динамических усилий в сечениях канатов в режиме торможения с результатами, полученными в SolidWorks/Motion для многоканатного подъема глубиной Н = 1025 м, оборудованного подъемной
машиной МПМН 6,3*2 со скипами 2СН 9,5-2.
Значения параметров пятимассовой системы мно-
гоканатной подъемной установки, представленной на
рисунке 1, приведены в таблице 1.
Графики усилий в упругих элементах пятимассо-
вой системы, рассчитанные в пакете MathCad, пред-
ставлены на рисунке 3. Из приведенных графиков
(рис. 3) видно, что процесс торможения сопровожда-
ется интенсивными колебаниями усилий в ветвях,
которые имеют явно выраженный затухающий ха-
рактер. Время торможения вращающейся массы mвр,
после остановки которой все тела системы начинают
колебаться относительно своих положений равнове-
сия, составляет примерно 6,5 с.
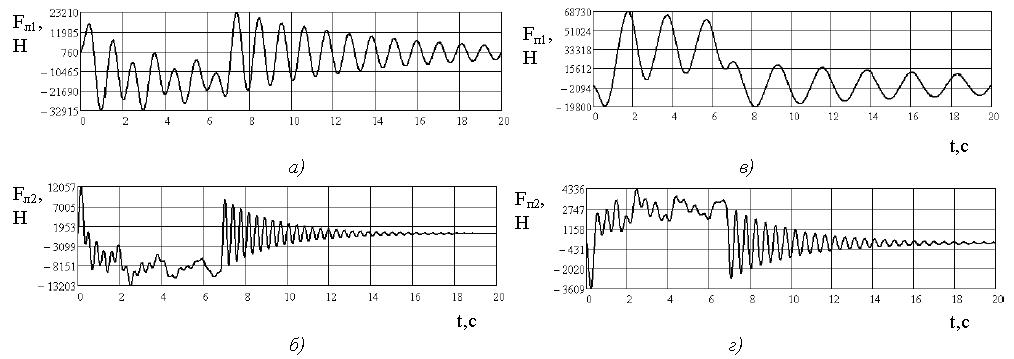
Рис. 3. Графики усилий в упругих элементах пятимассовой системы, рассчитанные в пакете MathCad:
а) в левой ветви для массы mл1; б) в левой ветви для массы mл2;
в) в правой ветви для массы mл1; г) в правой ветви для массы mп2
Полные усилия в верхних сечениях головных ка-
натов определяются по формулам

(11)
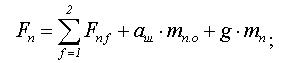
(12)
где
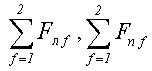
– сумма усилий в упругих эле-
ментах левых и правых осцилляторов соответственно.
На рисунке 4 представлены графики изменений
полных усилий в верхних сечениях канатов. Видно, что
усилия в канатах достигают максимума после 6,5 с, в
момент остановки барабана подъемной установки.
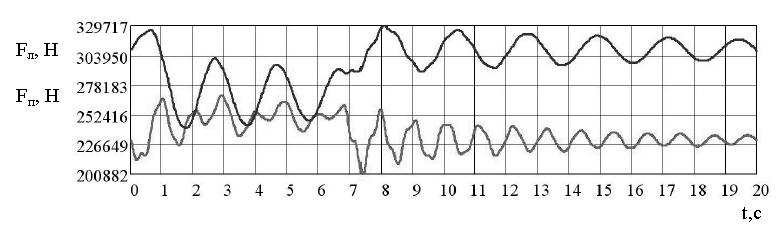
Рис. 4. Полные усилия в верхних сечениях канатов
Наибольшие усилия в левой спускаемой ветви с
грузом достигают 3,3·105Н. Колебания имеют затухающий характер. Анализируя полученные графики
полных усилий следует отметить, что основная частота колебаний имеет преобладающий характер.
Влияние, которое оказывают на нее другие частоты, незначительно и ими можно пренебречь.

Рис. 5. Отношение усилий в верхних сечениях канатов для определения условия отсутствия проскальзывания каната по шкиву трения
Для проверки условия отсутствия проскальзывания каната по шкиву трения были рассчитаны и построены графики функций
(рис. 5), представляющие отношения усилий в верхних сечениях канатов, а также график максимально
допустимого отношения по условию отсутствия проскальзывания каната по шкиву трения
Так как максимальные значения функций y1( t ) и
y2( t ) не превышают предельно допустимого по условию отсутствия проскальзывания канатов значения функции E( t ) (рис. 5), то проскальзывания канатов
по поверхности шкивов трения в процессе торможения не произойдет.
С целью проверки правильности результатов, полученных при моделировании процесса торможения
многоканатной машины в программе MathCad, был
выполнен расчет динамики пятимассовой системы в
программе SolidWorks/Motion.
В графическом редакторе SolidWorks была создана твердотельная модель пятимассовой системы динамического аналога подъемной установки, представленная на рисунке 6.
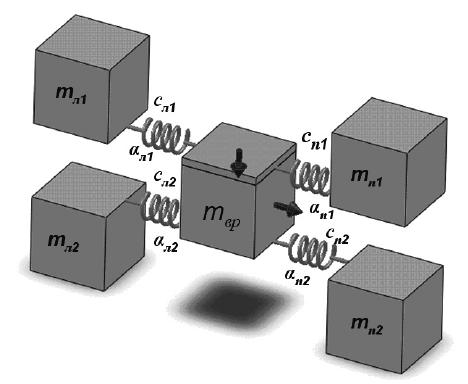
Рис. 6. Твердотельная модель динамического аналога многоканатной подъемной установки
Все массы соединены упруго-демпфирующими
элементами, для моделирования которых был использован инструмент „Пружина“ со свойствами
пружины растяжения-сжатия и возможностью задания коэффициента демпфирования.
При создании сборки пятимассовой твердотельной
модели между боковыми и нижними гранями кубических тел, имитирующих сосредоточенные массы системы, задавалось сопряжение „Совпадение“ для того,
чтобы каждое из тел имело только одну степень свободы.
Различные значения масс кубических тел, имеющих одинаковый объем, задаются в массовых характеристиках соответствующей величиной плотности
материала параметром „Массовая плотность“. Масса
среднего кубического тела mвр равна суммарной массе mвр + mл3 + mп3= 44752 кг.
Над средней массой mвр расположена прямоугольная плита (рис. 6), имитирующая тормозную колодку
дискового тормоза.
В SolidWorks/Motion значение тормозной силы,
прикладываемой к верхней грани прямоугольной
плиты (рис. 2), задавалось в виде функции времени
введением в командной строке выражения.
Для обеспечения выполнения функции торможения
прямоугольной плите заданы необходимые сопряжения: перемещение плиты зафиксировано и может происходить только по нормали к направлению движения
средней массы mвр; между нижней гранью прямоугольной плиты и верхней гранью массы mвр задано
сопряжение „Совпадение“ и установлен коэффициент
трения, равный 0,3.
IF(TIME-0.3: 0, (3*100000*(1-EXP((-TIME+0.3)/0.493)))
/0.3,(3*100000*(1-EXP((-TIME+0.3) /0.493)))/0.3)
При выборе вкладки „Анализ движения“ в про-
грамме SolidWorks/Motion для каждого тела твердотельной пятимассовой модели задавались начальные
скорости: л1 л2 вр п1 п2 x , x, x , x , x . Так как перед началом торможения подъемные сосуды движутся равномерно, то скорость всех тел принималась равной
7,5 м/с. Был рассмотрен режим спуска груза, как наиболее опасный случай работы многоканатной шахтной подъемной машины.
После запуска расчета параметров движения в графическом окне программы SolidWorks/Motion происходит визуализация перемещений тел пятимассовой модели. Вывод графических зависимостей усилий в упругих
элементах производится из вкладки PropertyManager выбором в категории „Силы“ результирующего компонента „Х-составляющая“ и в качестве определяющего компонента указанием на требуемый упругий элемент.
В результате получены графики усилий, действующих в упругих элементах при торможении, которые представлены на рисунке 7.

Рис. 7. Графики усилий в упругих элементах пятимассовой системы при моделировании
процесса торможения многоканатной подъемной установки в SolidWorks/Motion:
а) в левой ветви для массы mл1; б) в левой ветви для массы mл2;
в) в правой ветви для массы mл1; г) в правой ветви для массы mп2
Как видно из приведенных на рисунках 3 и 7 графиков, результаты моделирования в MathCAD идентичны
результатам расчетов в пакете SolidWorks/Motion.
Ошибка при определении величин усилий в упругих
элементах пятимассовой системы не превышает 4%,
что говорит о правильности полученных результатов.
Анализируя систему (4) и выражение тормозного
момента (5) видно, что при заданных условиях подъема груза, выбранном типе подъемной установки и постоянных значениях параметров, приведенных в
табл. 1 на динамические свойства системы оказывают
влияние три основных фактора: коэффициент массивности m подъемной установки, постоянная времени
тормоза ТF и время холостого хода тормоза tх.х.
Тормозную систему характеризуют следующие
параметры:
tх.х – время холостого хода тормоза, регламентируется правилами безопасности. Для действующих
подъемных установок tх.х > 0,5, для вновь создаваемых tх.х > 0,3;
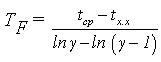
– постоянная времени тормоза, характеризующая интенсивность приложения тормозного усилия;
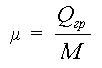
– коэффициент массивности подъемной
установки, м/сек2 [2].
Определим зависимость кратности тормозного
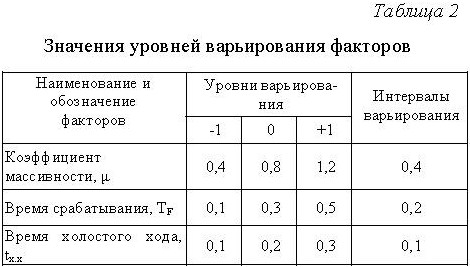
момента y от трех параметров: коэффициента массивности m подъемной установки, постоянной времени тормоза ТF и времени холостого хода тормоза tх.х,
значения которых приведены в таблице 2.
Аппроксимирующие уравнения кратности тормозного момента для случаев подъема и спуска груза
имеют вид
Определена погрешность интерполяции. Неточность интерполяционной формулы оценена абсолютной среднеквадратической e и максимальной относительной B погрешностями:
– абсолютная среднеквадратическая погрешность
определения кратности тормозного момента при
подъеме груза
– абсолютная среднеквадратическая погрешность
определения кратности тормозного момента при
спуске груза
– максимальная относительная погрешность определения кратности тормозного момента при подъеме груза
– максимальная относительная погрешность определения кратности тормозного момента при спуске груза
Небольшая максимальная относительная погрешность служит основанием для такого заключения: полученная функция интерполяции является удовлетворительной математической моделью кратности тормозного момента многоканатной подъемной машины.
Используя разработанную математическую модель были получены графики зависимости коэффициента запаса тормозного момента от коэффициента
массивности подъемной установки, приведенные на рис. 8.
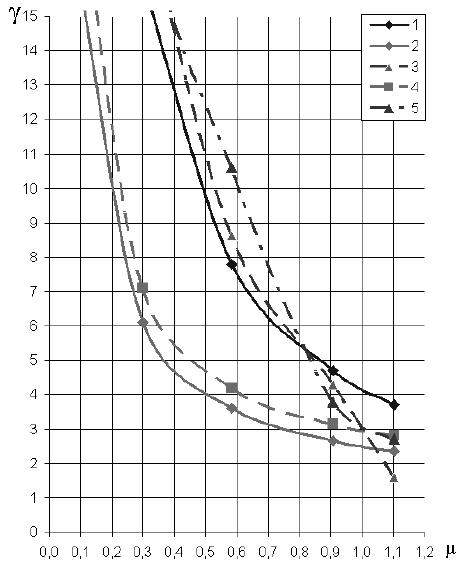
Рис. 8. Зависимость коэффициента запаса тормозного момента от коэффициента массивности подъемной установки
Линии 1 и 2 на графике соответствуют линиям
Мm max и Мm min, полученных Димашко А.Д. для
режимов торможения при подъеме груза с ускорением 5 м/с2 и спуске груза с ускорением 1,5 м/с2.
Линия 3 соответствует торможению при подъеме
груза, ниже которой соблюдается условие отсутствия проскальзывания каната по шкиву. Линия 4 соответствует торможению при спуске груза, при котором соблюдается минимально допустимое ускорение замедления 1,5 м/с2, а также выполняется условие отсутствия проскальзывания каната по шкиву.
Линия 5 соответствует торможению при спуске груза, ниже которой соблюдается условие отсутствия
проскальзывания каната по шкиву.
Диаграмму можно разбить на 3 зоны. В первой
зоне 0,1 < m < 0,8 величина кратности тормозного
усилия y ограничивается линиями подъема груза 3 и
спуска груза 4.
Во второй зоне 0,8 < m < 1,0 величина кратности
тормозного усилия y ограничивается линией 5 спуска
груза с максимально допустимым ускорением и линией 4 для спуска груза с минимально допустимым
ускорением 1,5 м/с2.
В третьей зоне m > 1,0 необходимо применять
тормозную систему со ступенчатым изменением
тормозного усилия.
Выводы
В результате проведенного исследования
была решена актуальная научная задача по
обоснованию параметров дискового тормозного
устройства для многоканатной шахтной подъемной
установки. Для расчетного случая шахтная подъемная
установка со шкивом трения – твердое тело и
тормозное усилие прикладывается дискретно,
допустимое соотношение между коэффициентом
запаса тормозного момента y и коэффициентом
массивности m, определенное из условия отсутствия
переподъема сосуда (азам>1,5м/с2), определяется с
погрешностью 10–15%, а из условия отсутствия
набегания сосуда на канат (азам<5 м/с2) – 12–15%.
При использовании модели шахтной подъемной
установки со шкивом трения в виде твердого тела с
дискретным приложением тормозного усилия, погрешность в определении области использования
тормозных систем с одноступенчатым регулированием может составлять 30–40%.
Допустимое соотношение между коэффициентом
запаса тормозного момента y и коэффициентом массивности ? необходимо определять для шахтной
подъемной установки со шкивами трения, как системы с распределенными параметрами с учетом плавности нарастания тормозного момента и ограничением по проскальзыванию каната по шкиву.
Наибольшие допустимые значения коэффициента
y при заданном коэффициенте m необходимо определять для расчетного случая подъем груза для m < 0,8 и
спуск груза m > 0,8.
Для шахтных подъемных установок со шкивом трения при коэффициенте массивности m > 1 необходимо
регулировать настройки предохранительного торможения в зависимости от спуска или торможения груза.
Список литературы
- Трибухин В.А. Обоснование параметров и режи
мов торможения шахтных подъемных машин с мно
гомодульным дисковым тормозом: автореф. дис. на
соискание научн. степени канд. техн. наук: спец.
05.05.06 „Горные машины“ / Трибухин Валерий Ана
тольевич; НИИ горной механики им. М.М.Федорова
(НИИГМ им. М.М.Федорова).– Донецк, 2003. – 16 с:
ил., табл. – Библиогр.:с. 17–18.
- Димашко А.Д. Шахтные электрические лебедки и
подъемные машины / Димашко А.Д., Гершиков И.Я.,
Кревневич А.А. – М.:Недра, 1973. – 310 с.
- Вертикальный транспорт на горных предприятиях
/ [Потураев В.Н., Червоненко А.Г., Колосов Л.В.,
Безпалько В.В.] – М.:Недра, 1975. – 351с.
НАЗАД К БИБЛИОТЕКИ

 (1)
(1) (2)
(2)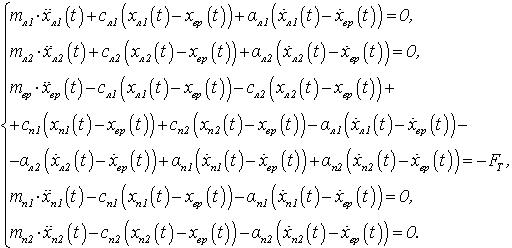 (3)
(3) (4)
(4)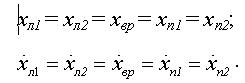

 (6)
(6) (7)
(7)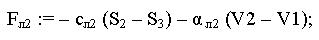 (8)
(8)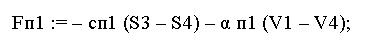 (9)
(9) (10)
(10)

 (11)
(11)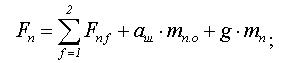 (12)
(12)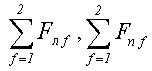 – сумма усилий в упругих эле-
ментах левых и правых осцилляторов соответственно.
– сумма усилий в упругих эле-
ментах левых и правых осцилляторов соответственно.

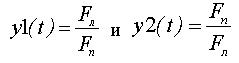
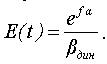


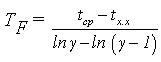 – постоянная времени тормоза, характеризующая интенсивность приложения тормозного усилия;
– постоянная времени тормоза, характеризующая интенсивность приложения тормозного усилия;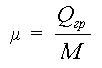 – коэффициент массивности подъемной
установки, м/сек2 [2].
– коэффициент массивности подъемной
установки, м/сек2 [2].