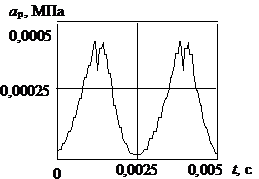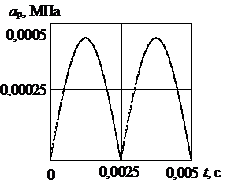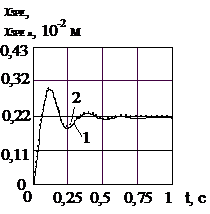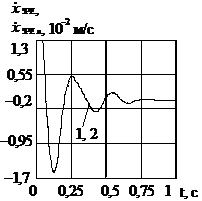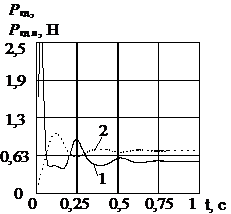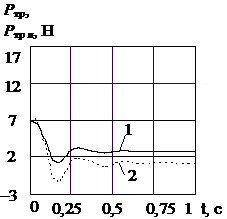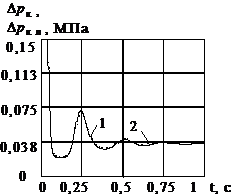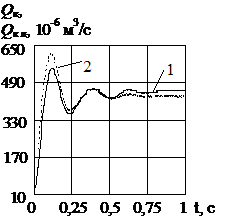УДК 621.22

ОБГРУНТУВАННЯ ПРАВОМІРНОСТІ ДОСЛІДЖЕННЯ ХАРАКТЕРИСТИК ГІДРОАПАРАТІВ З ГІДРАВЛІЧНИМ ВІБРАЦІЙНИМ КОНТУРОМ ПО ЇХ ЛІНЕАРІЗОВАНИМ МАТЕМАТИЧНИМ МОДЕЛЯМ

З. Я. Лур’є, доктор технических наук, професор, Андренко П. Н., доктор технических наук, професор, Национальный технический университет «ХПИ».

Источник: Сборник трудов Национального технического университета «ХПИ» «Весник ХПИ», Харьков, 2009г.

В статье приведена новая математическая модель переливного клапана с гидравлическим вибрационным контуром. Обоснована правомерность исследования динамических характеристик гидроппаратов с гидравлическим вибрационным контуром по их линейным математическим моделям. Это позволит использовать линейные математические модели таких гидроаппаратов в современных методах анализа и синтеза гидроагрегатов.

1. Вступ

Використання в гідроагрегатах гідроапаратів (ГА) з гідравлічним вібраційним контуром (ГВК) дозволяє підвищити їх динамічні характеристики, скоротити енергоспоживання, значно спростити систему керування. Динамічні характеристики таких ГА мало досліджені, що стримує їх широке використання в сучасних гідроагрегатах. Стосовно таких ГА актуальною є задача створення наукових положень і методологічного забезпечення методів математичного моделювання і розрахунку процесів, що в них протікають.

2. Аналіз публікацій

Теорія лінійних систем містить достатній арсенал різних методів аналізу і синтезу, які дозволяють забезпечити високі показники якості перехідних процесів (статичних і динамічних характеристик) проектованих пристроїв та систем. Причому математичні моделі, що описують динамічні процеси в часовій області, можуть бути однозначно представлені в частотній області. Останнє дуже важливо для виключення при проектуванні систем, резонансних явищ, викликаних зближенням власних частот з частотами керуючих сигналів і взбурень. За допомогою перетворення Лапласа лінійна (лінеаризована) модель представляється сукупністю передатних функцій типових ланок, структурною схемою на їх базі, це полегшує пошук рішення. Можлива векторно-матрична форма рівнянь моделі для реалізації модального керування (керуванням розташуванням коренів характеристичного рівняння лінеаризованой моделі). На базі лінійної моделі можна поліпшити динамічні характеристики досліджуваного об'єкта шляхом уведення ПІД-регулятора, синтезу пристроїв корекції з спостерігачем стану та ін. [1, 2]. Теорія нелінійних систем ще не одержала повного завершення. Тому ряд дослідників, розробивши нелінійні моделі конкретних об'єктів [3, 4, 5], піддають їх лінеаризації. При такому підході нелінійні функції, що входять у рівняння, що описують роботу проектованих пристроїв і систем, заміняють лінійними членами розкладу в ряд Тейлора, відкидаючи члени другого і більш високого порядку. У результаті отримують лінійну модель у відхиленнях щодо стану рівноваги (точки лінеаризації). Крім цього, для лінеаризації нелінійних рівнянь, що описують роботу пристроїв і систем, знайшов широке застосування метод гармонічної лінеаризації.

Лінійні математичні моделі гідроагрегатів дозволяють одержати аналітичні рішення, найбільш важливою перевагою, яких є можливість оцінити вплив фізичних параметрів, початкових і граничних умов на характер рішення [6]. Крім цього, більшість сучасних методів аналізу і синтезу гідроагрегатів базуються на лінійних математичних моделях, використання яких дозволяє досить легко і швидко провести вибір його конструктивних параметрів, вибрати структуру і параметри коригуючої ланки, забезпечити необхідну якість процесу регулювання.

Для правомірності використання лінійних математичних моделей ГА з ГВК при розробці методів їхнього проектування, з'явилася необхідність провести порівняльну оцінку близькості рішень, отриманих з використанням лінійних і нелінійних математичних моделей гідроагрегатів. Аналіз літературних джерел, проведений нами, дозволив встановити, що в них відсутня інформація, щодо обґрунтування правомірності дослідження характеристик ГА з ГВК по їх лінеарізованим математичним моделям.

3. Постановка завдання

Метою статі є обґрунтування правомірності дослідження характеристик ГА з ГВК по їх лінеарізованим математичним моделям.

4. Порівняльний аналіз перехідних процесів у ГА з ГВК, отриманих по їх нелінійній і лінійної математичних моделях

Його проведемо на прикладі математичної моделі гідроагрегата з переливним клапаном прямої дії з ГВК (рис. 1). Робоча рідина (РР) від насоса з постійною подачею надходить до споживача з витратою .

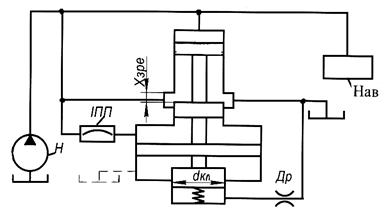
Рис. 1. Схема гідроагрегата з переливним клапаном прямої дії і ГВК: Н – насос; ІПП - інтерференційний підсилювач пульсацій; Др – дросель; Нав – навантаження

Помітимо, що на виході з насоса з постійною подачею, у силу зміни об’ємів його камер нагнітання, має місце пульсації витрати РР (визначаються його кінематикою і геометричними розмірами) і викликають пульсацію тиску. Надлишок РР , зливається через дроселюючу щілину клапана з ГВК у бак. При розгляді гідроагрегата вважаємо, що трубопроводи мають великий діаметр, а процеси, у що в них відбуваються описуються без врахування розподілу параметрів РР по довжині. Це дозволяє не розглядати хвильові процеси.

4.1. Нелінійна математична модель

При розробці математичної моделі гідроагрегата приймалося наступне: виконується рівняння нерозривності течії РР; кавітація відсутня; втрати тиску в трубопроводах незначні; температура і щільність – РР постійні і рівні їхнім середнім значенням.

Математична модель гідроагрегата представлена:

– рівнянням руху ЗРЕ клапана

, (1)

– рівнянням нерозривності

, (2)

– рівнянням витрати на виході з насоса

, (3)

де – об'ємний ККД насоса; – геометрична подача пластинчастого насоса, що розраховується по залежності [7]

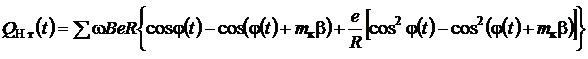. (3а)

У рівняння (3а) входять наступні величини: і – кутова швидкість обертання і кут повороту ротора; R і B – радіус і ширина статора; e – ексцентриситет насоса; – кут між пластинами; – число камер, що одночасно знаходяться в зоні нагнітання.

Рівняння (1) – (3) розглядаються разом з рівняннями, що описують зміни навантаження на виході з гідроагрегату, початковими умовами.

Істотною нелінійністю в математичній моделі клапана є сила тертя, яка є сумою сил сухого тертя, обумовленого нерівномірністю дії сил пружин, і сили рідинного тертя

, (4)

де і – відповідно сили сухого і рідинного тертя; – функція Крон екера; – переміщення ЗРЕ клапана.

Сила сухого тертя [8] , де – радіальна сила, викликана перекосом пружини; – коефіцієнт тертя, значення якого наведено в [8].

Вважаючи, що ЗРЕ займає асиметричне положення і має точки контакту з гільзою, а кут його перекосу зневажливо малий, використовуючи залежність для обліку зсуву пружини щодо її осі, наведену в [9], радіальну силу розраховуємо по формулі

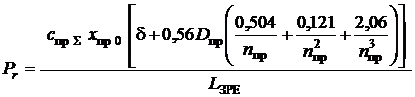де – сумарна жорсткість пружин; – попередній підтиск пружини; – радіальний зазор; , – відповідно зовнішній діаметр і кількість робочих витків пружини; – довжина ЗРЕ.

Тоді залежність для визначення сили сухого тертя можна представити у вигляді

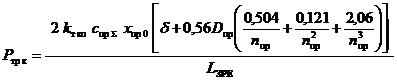. (5)

Сила рідинного тертя [10]

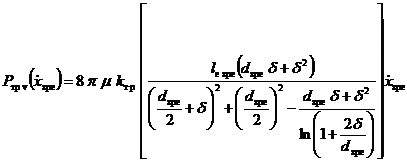, ₍₆₎

де – коефіцієнт динамічної в'язкості РР; – ефективна довжина контакту між ЗРЕ і гільзою; - коефіцієнт, що характеризує положення ЗРЕ в гільзі, і визначається по уточненій нами залежності з роботи [8] ,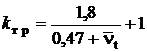

де – відносний коефіцієнт кінематичної в'язкості РР, .

Нелінійною, залежною від коефіцієнта витрати і перепаду тисків на дроселюючий щілини, є гідродинамічна сила [1]

, (7)

де – коефіцієнт, що враховує осциляцію ЗРЕ, приведений нами в [11]. Інші коефіцієнти розраховувалися згідно залежностей [1]

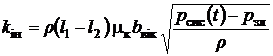і . (8)

Тут: – ширина вікон у втулці клапана; – тиск у гідроагрегаті з урахуванням пульсацій (мал. 2 а); – тиск зливу; – кут нахилу вектора потоку РР до осі ЗРЕ клапана; – щільність РР; і – відповідно, відстані від вікна у втулці клапана до осі каналу живлення і до осі каналу зливу.

Коефіцієнт витрати визначався по залежності [8]

де – граничне значення коефіцієнта витрати клапана; Re_к – коефіцієнт корекції.

Сила пружини обчислювалася по формулі

, (9)

Сила рідинної пружини обчислювалася по [12]

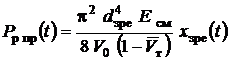, (10)

де – приведений модуль об'ємної пружності трубопроводу с РР, розрахований з врахуванням газовмісту та пружних властивостей трубопроводу; V₀ – об’єм РР у порожнинах клапана при середньому положенні ЗРЕ; – відносний об’єм трубопроводів і порожнин клапана; V_т – об’єм РР, що знаходиться в трубопроводах від насоса, до споживача і клапана.

Сила, під дією якої відбувається осциляція ЗРЕ, розраховувалася по залежності

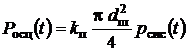, (11)

де – коефіцієнт підсилення ГВК.

Сила керування розраховувалася по залежності

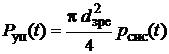. (12)

Сила демпфірування визначалася з залежності

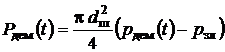, (13)

де – тиск у порожнині демпфірування.

Зневажаючи стискальністю РР у порожнині демпфірування, і прирівнюючи витрату через дросель, демпфера , витраті керування клапаном

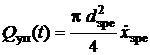, (14)

визначаємо тиск у ній

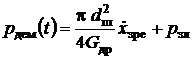, (15)

де – провідність ламінарного дроселя.

Витрата РР у клапані розраховувався по залежності

_.₍₁₆₎

Виразимо формулу (16) через параметри клапана

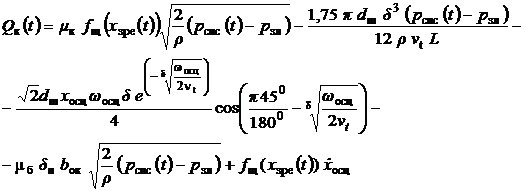,(17)

де – площа дросселюючої щілини клапана; – коефіцієнт кінематичної в'язкості РР; – довжина перемичок у корпусі клапана; і – відповідно, амплітуда і частота осциляції ЗРЕ; , – відповідно зазор і коефіцієнт витрати при течії РР через цей зазор, утворений у результаті перекриття робочого вікна клапана.

Витрата стиску 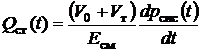. (18)

Похідна тиску РР у нагнітальній магістралі з урахуванням рівнянь (2) і (18) визначається по

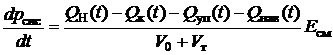. (19)

Розроблена математична модель гідроагрегата з переливним клапаном прямої дії з ГВК (1) – (18), є нелінійною через нелінійність рівнянь (4), (7), (17). З функціонування гідроагрегата видати, що перехідні процеси в ньому виникають за рахунок зміни витрати навантаження. Після закінчення перехідних процесів швидкість ЗРЕ клапана = 0, а приймає значення, при якому клапан зливає в бак різницю витрат РР між навантаженням і насосом. Якщо розв’язати систему рівнянь (1) – (19) щодо однієї перемінної (, чи ), то отримаємо нелінійне диференціальне рівняння 3-го порядку. Для одержання єдиного рішення якого необхідно задати 3 початкові умови. За початкові умови в режимі розгону гідроагрегата при ступінчастому сигналі приймалися умови , і . Тиск зливу , вважали рівним нулю.

Величина в усталеному режимі, відповідає навантаженню на гідродвигуні, що трансформується витратою . Змінюючи вхідний сигнал при заданих початкових умовах, одержували графіки перехідних процесів у гідроагрегаті.

4.2. Лінеаризована математична модель

Одержання цієї моделі на базі нелінійної моделі гідроагрегата базується на лінеаризації рівнянь (4), (7) і (17). Піддаючи перший нелінійний доданок виразу (4) (сила сухого тертя) гармонічної лінеаризації з урахуванням роботи [1], одержуємо

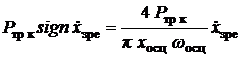, (20)

де розраховувалася по формулі (5). Другий доданок є лінійним і залишається без змін (див. формулу (6)).

Лінеаризація рівнянь (7) і (17) проводилася в точці, що відповідає половині ходу ЗРЭ для заданої витрати навантаження. Коефіцієнт витрати приймався постійним і рівним його значенню в точці лінеаризації. Розкладаючи функції описані даними рівняннями в ряд Тейлора і зневажаючи членами які містять відхилення в ступені вище першої одержали:

лінеаризоване рівняння гідродинамічної сили

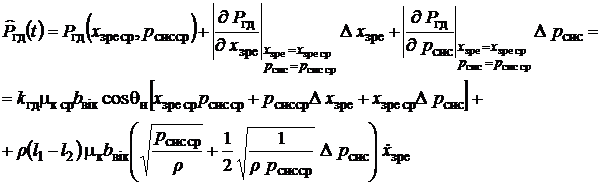, (21)

лінеаризоване рівняння витрати через клапан

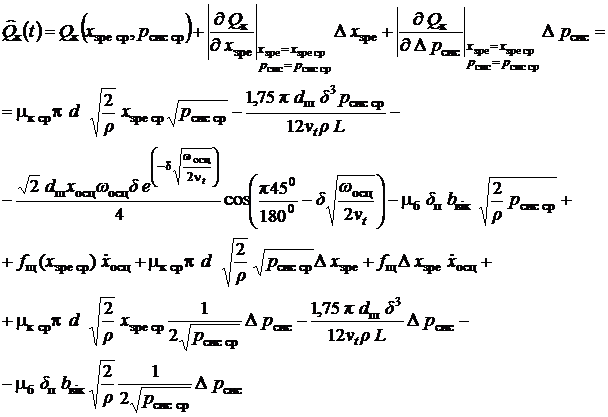.(22

де ; ; індекс ср відноситься до значень, визначених у точці лінеаризації;

4.3. Порівняльний аналіз перехідних процесів у гідроапаратах з ГВК, отриманих по їх нелінійної та лінійної математичних моделях

Його проводили по графіках перехідних процесів переміщення ЗРЕ, швидкості ЗРЕ, гідродинамічної сили, сили тертя, тиску та витрати на виході клапана, отриманих на персональному комп'ютері за допомогою пакета прикладних програм. Досліджували клапан прямої дії з ЗРЕ, який має гостру дроселюючи кромку мм; = 70 Н/мм; m = 0,14 кг; = 1,5 мм; = 8 мкм; = 13 мм;, = 5; =55 мм; = 4,5 мм; =31,4 мм; = 0; = 0,7; ; =1,3; =1,12; = 0,2 [8]; РР – масло ІГП – 30, газовміст якої – 1, 0%.

Витрата на виході з насоса була прийнята постійною, а сила, під дією якої відбувається осциляція ЗРЕ, визначається по залежності

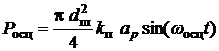. (23)

Тут – амплітуда пульсації тиску в гідроагрегаті, розрахована з рівності енергій імпульсів пульсацій на виході з насоса і моделюючих синусоїдальних гармонічних впливів (рис.2 б).


а	б

Рис.2. Пульсації тиску в гідроагрегаті: а – на виході з пластинчастого насоса НПЛ 40/6,3 (нелінійна модель); б – моделюючих (лінійна модель)

Помітимо, що при цьому частота осциляції дорівнює частоті пульсацій тиску на виході з насоса. Інші величини визначалися аналогічно, як і в нелінійній математичній моделі. Однаковими були і початкові умови.

Для оцінки близькості перехідних процесів клапана використовували відносну інтегральну оцінку

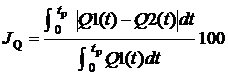%, (23)

де, як приклад узяті, і – відповідно витрати через клапан розраховані по нелінійній і лінійної математичних моделях; - час перехідного процесу.

Оцінка (23) характеризує відношення значень різних площ під кривими і до площі під кривою за час перехідного процесу . Аналогічно до (23) прийняті вирази для інших змінних.

Характер перехідних процесів витрати і тиску на виході клапана, а також переміщення його ЗРЕ, його прискорення, зміна гідродинамічної сили і сили тертя, розрахованих по його нелінійній і лінійній математичних моделях, показали досить гарний збіг (рис. 3). Параметри, що змінювалися в процесі досліджень і відносні інтегральні оцінки (індекс позначає параметр по який розрахована відносна інтегральна оцінка) наведені в табл. 1.

Таблиця 1

Результати розрахунку відносної інтегральної оцінки переміщення ЗРЕ, площі дроселирующей щілини, витрати і тиску на виході клапана з ГВК, розраховані по нелінійній і лінійної математичних моделях, = 901 (f = 200 Гц; f = 150 Гц; f = 250 Гц; f = 300 Гц)

,	,%	,%	,%	,%	,%	,%	,%
650	4,09	8,92	11,49	35,47	43,79	6,46	2,74
550	3,28	7,49	7,07	28,4	39,15	5,84	2,73
450	2,77	6,83	4,51	15,23	34,83	5,47	1,07
450	2,71	7,88	4,45	15,24	33,28	5,44	1,07
450	2,8	6,26	4,54	15,13	35,77	5,5	1,12
450	2,82	5,97	4,56	15,o	36,4	5,51	1,26
350	2,4	6,36	2,8	9,48	30,74	5,23	0,69
250	2,09	6,0	1,71	10,63	26,52	5,08	0,7
150	1,84	5,66	0,97	8,59	23,28	5,0	0,35

Графіки перехідних процесів клапана, а саме переміщення ЗРЕ, швидкості ЗРЕ, гідродинамічної сили, сили тертя, тиску та витрати на виході клапана, отриманих по нелінійним і лінеарізованим математичним моделям клапана показали гарний збіг. Максимальне значення відносної інтегральної оцінки витрати і тиску на виході клапана при заміні нелінійної математичної моделі лінеарізованою не перевищує для витрати 7%, і для тиску - 3%. Найбільшу відносну інтегральну оцінку, при гарному збігу характеру змін, має сила тертя. Що можна пояснити використанням різних його моделей. Помітимо, що зі збільшенням відкриття ЗРЕ клапана (збільшенням витрати навантаження) відносні інтегральні оцінки збільшуються. Це очевидно, і обумовлюється збільшенням ходу ЗРЕ клапана на якому робимо лінеаризацію. Близькість графіків перехідних процесів обумовлюється використанням ГВК, що здійснює самолінеарізацію сил сухого тертя. Якщо вважати, що відхилення ЗРЕ клапана від його сталого значення не перевищує одного десятої від його повного ходу, то відмінність вихідних параметрів клапана (витрати і тиску) розрахованих по нелінійній математичній моделі від лінеарізованої не перевищують 1%. Отже, розгляд клапана як лінійного елемента є цілком правомірним.


а	б

в	г

д	е

Рис. 3 Графіки перехідних процесів клапана, розраховані по його нелінійній – 1 і лінійній – 2 математичним моделям, при = 901 , : а – переміщення ЗРЕ; б – швидкість ЗРЕ; в – гідродинамічна сила; г – сила тертя; д – тиск на виході клапана; е – витрата на виході клапана

5. Висновки

Графіки перехідних процесів клапана, отриманих по нелінійній і лінеарізованій математичним моделям клапана показали гарний збіг. Максимальне значення відносної інтегральної оцінки витрати і тиску на виході клапана при такій заміні не перевищує для витрати 7%, і для тиску - 3%. Таким чином, обґрунтована правомірність використання лінеаризованных математичних моделей для дослідження динамічних характеристик клапана з ГВК.

Література

1. Попов Д .Н. Динамика и регулирование гидро - и пневмосистем. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1987. – 464 с.

2. Автоматизированное проектирование машиностроительного гидропривода / И. И. Бажин, Ю. Г. Беренгард и др. под ред. С. А. Ермакова. – М.: Машиностроение, 1988. – 312 с.

3. Зайончковський Г. Й., Пархомчук С. І. Вплив пружності робочої рідини і обмеженої жорсткості опори кріплення гідравлічного слідкуючого рульового приводу на його стійкість і динамічні властивості // Промислова гідравліка і пневматика. – Вінниця: ВДАУ, 2004. – № 1(3). – С. 59 – 63.

4. Навроцкий К. Л. Теория и проектирование гидро- и пневмоприводов. – М.: Машиностроение, 1991. –384 с.

5. Зайончковский Г. Й. Оцінка стійкості і протифлатерних властивостей гідромеханічних рульових слідкуючи приводів // Промислова гідравліка і пневматика. – Віниця: ВДАУ, 2006. – №1 (11). – С. 53 – 58.

6. Фарлоу С. Уравнения с частными производными. Для научных работников и инженеров. – М.: Мир, 1985. – 384 с.

7. Башта Т. М. Гидравлические приводы летательных аппаратов. – М.: Машиностроение, 1967. – 495 с.

8. Данилов Ю .А., Кирилловский Ю. Л., Колпаков Ю .Г. Аппаратура объемных гидроприводов. – М.: Машиностроение, 1990. – 272с.

9. Хвингия М. В. Вибрация пружин. – М.: Машиностроение, 1969. – 287 с.

10. Электрогидравлические преобразователи гидравлических и газовых приводов / Под ред. Е. Н. Решетникова, Ю.А. Саблина, В. Е. Григорьева. – М.: Машиностроение, 1982. – 144 с.

11. Андренко П. Н. Расчет гидродинамической силы на осциллирующем золотнике гидроаппарата // Вестник НТУ “ХПИ”. – Харьков: НТУ “ХПИ”, 2002. – № 7, Т. 2. – С. 109 – 116.

12. Электрогидравлические следящие системы. Хохлов В. А., Прокофьев В. Н., Борисова Н. А. и др. Под ред. В. А. Хохлова – М.: Машиностроение, 1971. – 431 с.

Лур’є Зиновій Якович, доктор технічних наук, професор, кафедра Гідравлічні машини, Національний технічний університет “Харківський політехнічний університет”. 61002 Харків 2, вл. Фрунзе 21. тел. 707-61-28.

61000 Харків, вл. Анрі Барбюса, б. 6, кв. 40. Тел. 705- 34 -92.

Андренко Павло Миколайович, кандидат технічних наук, доцент, кафедра Гідропневмоавтоматика і гідропривод, Національний технічний університет “Харківський політехнічний університет”. 61002 Харків 2, вл. Фрунзе 21. тел. 707-61-28. 61174 Харков 174, пр. Победы 67 кв. 8. Тел. 337-62-68.