УДК 621 – 82

 

Математична модель гідророзподільника з новим вібраційним контуром

 

       І. П. Гречка,  ассистент. Національний технічний університет “Харківський політехнічний інститут”

 

     Источник: Сборник трудов Национального технического университета «ХПИ» «Весник ХПИ», Харьков, 2006г.

 

    Опис: У статті наведені результати розрахункових досліджень робочих процесів у гідророзподільнику, в яких для покращення динамічних характеристик використовується вібраційна лінеаризація. Проведен докладний аналіз схемних рішень гідророзподільників із гідравлічним вібраційним контуром, де для осциляції золотника використовується пульсація робочої рідини, що утворюється на виході об’ємної гідромашини. Побудові математичної моделі гідророзподільника з гідравлічним вібраційним контуром.

 

Вступ

Гідророзподільники (ГР), в яких для покращення динамічних характеристик використовується вібраційна лінеаризація, знайшли широке застосування в сучасних системах гідроприводів. Докладний аналіз схемних рішень таких ГР наведено в [1], а стосовно ГР із гідравлічним вібраційним контуром (ВК) у [2], де для осциляції золотника використовується пульсація робочої рідини, що утворюється на виході об’ємної гідромашини. Побудові математичної моделі ГР з гідравлічним ВК і присвячена стаття.

 

Аналіз публікацій

Математичним моделям ГР присвячена досить велика кількість наукових робіт [3 – 6]. Однак, наведені в них математичні моделі ГР не враховують параметрів осциляції золотника та їх вплив на його характеристики. Крім того, в науково-технічній літературі немає відомостей про розроблений новий гідравлічний ВК, за допомогою якого здійснюється осциляція золотника. Отже, побудова математичної моделі ГР з новим ВК, яка враховує параметри осциляції золотника, є актуальною науково-технічною задачею задачею.

 

Мета та задачі досліджень

Метою даної статті є отримання докладної математичної моделі ГР прямої дії з новим гідравлічним ВК, яка дозволить досліджувати вплив конструктивних і робочих параметрів на його характеристики.

 

Гідророзподільник із новим гідравлічним вібраційним контуром

ГР із новим гідравлічним ВК збудовано на базі ГР з гідравлічним управлінням, у камерах управління якого розміщені пружини з різною жорсткістю, причому, камера управління, в якій розміщена пружина з меншою жорсткістю, з'єднана з виходом гідромашини, через підсилювач пульсацій тиску (реалізується гідравлічний ВК). Як підсилювач пульсацій тиску пропонується використовувати гідравлічну місткість, конструктивні параметри якої підібрані належним чином. Коефіцієнт підсилення такого ВК є самостійним науково-технічним завданням, яке в даній роботі розглядати не будемо. На рис. 1 наведено розрахункову схему для визначення параметрів осциляції золотника ГР.

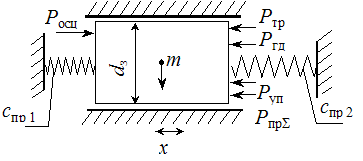
Рис. 1. Схема для розрахунку параметрів осциляції золотника гідророзподільника

 

Припущення

Вважаємо, що виконується умова нерозривності робочої рідини та відсутня кавітація. Робоча рідина – масло ІГП – 30 при постійній температурі, рівній 50 ˚С, в якому кількість нерозчиненого повітря не перевищує 2%. Корпус ГР та золотник абсолютно жорсткі та виконані з однакового матеріалу, а жорсткість трубопроводу враховується при обчисленні приведеного модулю об'ємної пружності робочої рідини.

Так як пружини гідравлічного ВК мають невелику довжину та кількість робочих витків, вважаємо, що вони працюють у лінійному діапазоні своїх характеристик, та при роботі ГР не відбувається їх відрив від поверхонь контакту.

Параметри осциляції золотника (амплітуда та частота) такі, що швидкість його руху не перевищує деякої критичної, що обчислюється аналогічно, як в [7], і визначається в основному зусиллям контактного тертя, а його характеристика має вигляд сухого тертя.

Кут θ – відхилення потоку робочої рідини, що протікає через дроселюючу щілину ГР, постійний і дорівнює 69˚ [8]. Приймемо також, що зміна сили управління відбувається повільно, в порівнянні зі зміною сили, під дією якої відбувається осциляція золотника.

Вважаємо, що лінійні члени гідравлічної системи, мають властивості фільтра, що притаманно всім гідравлічним системам [9], тобто, при виникненні періодичних коливань всі вищі гармоніки, крім третьої, придушуються лінійною частиною фільтру.

Гідравлічний опір ГР складається з місцевих втрат у робочих вікнах і втрат у внутрішній порожнині. Розміри внутрішньої порожнини ГР невеликі, у порівнянні з розмірами трубопроводів, що підводять робочу рідину до ГР, і значно більше площі робочого вікна, тому основна частина гідравлічних втрат має місце в зазорі між робочими крайками золотникової пари. Коефіцієнт місцевих гідравлічних втрат визначається експериментально. У загальному випадку, він залежить від перепаду тиску та числа Рейнольдса. В літературі [5, 10], досить широко, представлені залежності зміни коефіцієнта опору від робочих і конструктивних параметрів ГР. Проведені оцінювальні розрахунки опору каналів ГР показали, що вони незначні, в порівнянні з утратами в дроселюючих щілинах ГР, навіть при їх повному відкритті, при якому власний опір каналів золотника максимальний, тому далі ними нехтуємо. Вважаємо також, що при рівних значеннях переміщення золотника, провідності дроселюючих щілин ГР рівні.

 

Математична модель гідророзподільника

При розгляді сил, що діють на золотник, приймаємо, що сила, під дією якої відбувається осциляція золотника, визначається рівнянням:

,                                      (1)

де S(s) – многочлен, який враховує параметри гідравлічного ВК та визначається з залежності:

,                                            (2)

де d_з – діаметр торця золотника в камері управління (камери, до якої підводиться тиск з гідравлічного ВК); Dp_т – максимальна амплітуда пульсацій тиску в цій камері; s – перетворювач Лапласа; A – амплітуда зовнішньої сили, що утворює осциляцію (3 – 5% від тиску з виходу гідромашини [11]); W_з – частота зовнішньої сили, що утворює осциляцію (частота пульсацій тиску на виході об'ємної гідромашини); t – час.

Сумарна сила від дії пружин визначається з залежності:

,                             (3)

де с_пр1, с_пр2 і с_прΣ – відповідно жорсткості 1 і 2 пружин і сумарна; х – переміщення золотника; с_{ж ср} – середній коефіцієнт жорсткості рідинної пружини, який при умові великого відносного об'єму трубопроводів та каналів , що, зазвичай, має місце у гідравлічному ВК, визначається з залежності [12]:

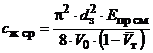,                                                   (4)

де Е_{пр см} – приведений модуль об'ємної пружності робочої рідини, з урахуванням нерозчиненого повітря, та пружності стінок трубопроводу; V₀ – об'єм робочої рідини, що знаходиться в кожній камері управління при середньому положенні золотника;  – відносний об'єм трубопроводів та камер управління: , де V_т – об'єм трубопроводів.

Силу тертя, при прийнятих допущеннях, вважаємо суттєво нелінійною та функцією часу, що визначається з залежності [7]:

,                                    (5)

де Р_{тр п} – сила тертя спокою; Р_r – радіальна сила, що діє на золотник (обумовлена несиметричною дією сили пружини); k_{тр к0} – коефіцієнт тертя, який визначається з [7].

Гідродинамічна сила визначається залежністю [8]:

,                                   (6)

де с_гд – коефіцієнт жорсткості гідродинамічної пружини, який визначається з [8] та при обчисленні якого коефіцієнт витрат визначали в залежності від критичного числа Рейнольдса за залежністю, наведеною у [13]; k_ін – коефіцієнт, що враховує інерційну дію несталого потоку на золотник [8].

Сила управління Р_уп=Р_уп (t) – у загальному випадку є функцію часу, величина якої може бути й постійною.

 

Гідравлічна характеристика гідророзподільника

Гідравлічна характеристика ГР отримана на підставі робіт [3–6, 10, 12], стосовно до розробленої конструкції, зображеної на рис. 2, без запропонованого гідравлічного вібраційного контуру.

Узагальнена гідравлічна характеристика ГР: Q_д = f(p_д, x).

При прийнятих допущеннях, із врахуванням параметрів ГР, аналогічно з [5], і приймаючи, що р_з = 0, узагальнена гідравлічна характеристика:

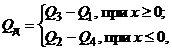                                              (7)

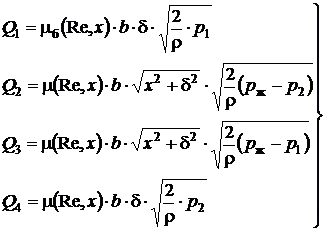,                      (8)

де μ(Re, x) – коефіцієнт витрати дроселюючої щілини, що визначається в залежності від числа Рейнольдса та критичного числа Рейнольдса [13]; μ_б (Re, x) – коефіцієнт витрати перекритого робочого вікна ГР, що визначається з [5]; b – довжина робочого дроселюючого вікна; r – щільність робочої рідини.

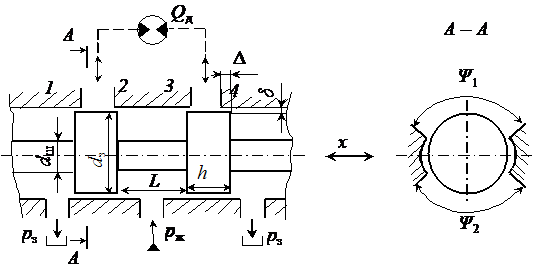
Рис. 2. Конструктивна схема гідророзподільника: 1 – 4 – дроселюючі кромки; х – переміщення золотника; Δ – перекриття; d_з і d_ш – відповідно діаметр золотника та шийки; h – ширина пояска золотника; ψ = Σψ_і – сумарний центральний кут вікна для втулки (ψ_max = 360˚); L – відстань між кромками золотника; р_ж, р_з – відповідно тиск живлення та зливу

 

Для ідеального ГР (в якого радіальний зазор дорівнює нулю, та який має нульове перекриття та рівні провідності дроселюючих щілин) залежність (7) з урахуванням (8) може бути записана в вигляді:

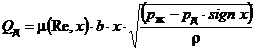,                                     (9)

де sign x – функція Кронекера; р_д – перепад тиску на виконавчому механізмі.

 

Математичний опис руху золотника

Рівняння руху золотника:

,                          (10)

де m – маса золотника та пов'язаних з ним елементів, еквівалентна маса пружини визначається з [14].

Відмітимо, що рівняння (10) справедливе при виконанні умови:

,                     (11)

при, тобто відсутності застою. Якщо при  виявиться, що , то рівняння (10) буде справедливе при , а при  почнеться застій золотника. Застій буде продовжуватися до тих пір, поки  не зміниться в межах:

, де * позначені значення сумарної сили пружин, обчислені для значення х, при якому відбулася зупинка золотника. Отже, як доповнення до вже прийнятих припущень, приймаємо, що застій золотника відсутній.

Для розв'язку рівняння (10) скористаємося методом вібраційної лінеаризації [9]. Приймаємо, що розв'язок (10) може бути наближено представлено в формі:

,                                        (12)

де а –амплітуда осциляції; j – фаза.

Спочатку розглянемо випадок, коли Р_уп(t) = 0. Виразимо складову, що входить до рівняння (1), через (12) і, проводячи гармонічну лінеаризацію сили тертя аналогічно, як зроблено в [9], після перетворень Лапласа запишемо її у вигляді:

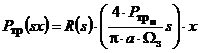                               (13)

де R(s) – многочлен, що враховує параметри вузлу тертя (для ГР дорівнює одиниці).

Підставимо (13) в (10), проведемо перетворення Лапласа, та зробимо підстановку s = j ^. Ω_з і отримаємо:

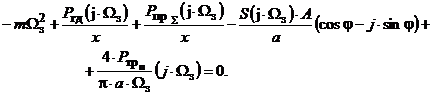         (14)

Розглядаючи параметри осциляції золотника, при х = 0, при додатньому його перекритті, підставляючи в (14) значення із (2) і (3), та розв'язуючи його відносно а і φ, отримаємо рівняння першого наближення для їх визначення:

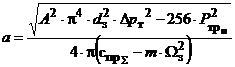,                               (15)

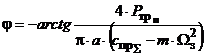.                                      (16)

Для випадку, коли золотник має нульове або від'ємне перекриття, при обчисленні (14) необхідно враховувати гідродинамічну силу (рівняння (6)), в цьому випадку його розв'язок в першому наближенні:

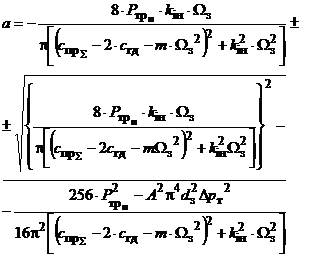                   (17)

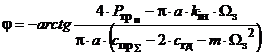і                                .                                            (18)

Відмітимо, що отримані розв'язки справедливі для золотника при виконанні умови захвату, яка визначається, як умова існування дійсного додатнього розв'язку для а в рівнянні (17).

Коли золотник має перекриття, вплив гідродинамічної сили, що діє на нього, необхідно враховувати з моменту, коли центр осциляції золотника буде більше величини перекриття.

Зауважимо, що для однієї однозначної непарно-симетричної нелінійності, з вищих гармонік, найбільш суттєво впливає третя. Тому, обмежимося розглядом процесу осциляції золотника, з урахуванням третьої гармоніки.

Припустимо, що на вхід системи діє синусоїдальна зовнішня сила, а розв'язок рівняння (10), що описує осциляцію золотника, будемо шукати за виразом [15]:

,                  (19)

де δ₃ і φ₃ – відповідно відносна амплітуда третьої гармоніки та її фазове зрушення.

Проводячи гармонічну лінеаризацію рівняння (14), з урахуванням (19), отримаємо рішення у вигляді:

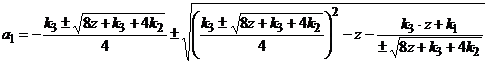,                (20)

де z – розв'язок кубічного рівняння.

,        (21)

де через k позначені коефіцієнти при відповідних членах алгебраїчного рівняння, що визначаються через параметри ГР та гідравлічного ВК.

З урахуванням розв'язку рівняння (18) знаходимо уточнений фазовий зсув:

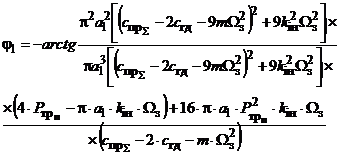,                   (22)

а також 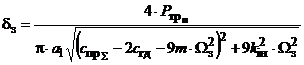                  ,                                   (23)

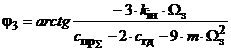.                                         (24)

Зробивши підстановку (22), (23) та (24) в (19) знаходимо амплітуду коливань золотника.

При наявності сигналу управління та при прийнятих припущеннях розв'язок (10), відповідно до прийнятого методу розв'язку, має вигляд:

,                                 (25)

де х⁰(t) – вільно змінна складова; х^* – коливальна складова.

В цьому випадку процеси, що відбуваються в ГР, у відповідності з прийнятою методикою, можуть бути розраховані за лінійним рівнянням:

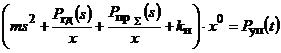,                    (26)

де k_н – коефіцієнт підсилення, який, у загальному випадку, залежить не тільки від структури та параметрів ГР, але й від амплітуди та частоти зовнішньої сили, який для ідеальної релейної характеристики [9]:

.                                                  (27)

Тоді остаточно (26) може бути записане в вигляді:

.                 (28)

Рівняння (8) разом із рівнянням (28), при прийнятих припущеннях, є повною математичною моделлю ГР з новим гідравлічним вібраційним контуром.

 

Висновки

Отримані залежності є повною математичною моделлю гідророзподільника з новим гідравлічним вібраційним контуром, яка враховує такі фактори, як параметри осциляції золотника, стисливість робочої рідини, її газовміст, пружність трубопроводів і інші. Результати чисельного рішення математичної моделі дозволить виконати раціональний вибір робочих і конструктивних параметрів такого гідророзподільника.

 

Література

1. Андренко П. Н. Вибрационная линеаризация – эффективный путь улучшения динамических характеристик гидроаппаратов // Вибрация в технике и технологиях. – № 2 (28). – Винница ВДАУ. – 2003. – С. 39 – 45.

2. Андренко П. Н. Принцип построения гидравлических аппаратов нового класса // Вестник Национального технического университета ”Харьковский политехнический институт”. Харьков: НТУ “ХПИ”. Вып. 129. – Ч.2. – 2001– С. 102 – 106.

3. Башта Т. М. Гидропривод и гидропневмоавтоматика. – М.: Машиностроение. 1972, – 320с.

4. Чупраков Ю. И. Гидропривод и средства гидропневмоавтоматики. – М.: Машиностроение. 1979, – 232 с.

5. Гамынин Н. С. Гидравлический привод систем управления. – М.: Машиностроение. 1972, – 376 с.

6. Андренко П. М. Проектування і розрахунок елементів та пристрів гідропневмоавтоматики: Навч. посібник. – К. УМК ВО, 1990. – 100 с.

7. Андренко П. Н., Кулинич А. В. Определение силы трения на запорно-регулирующем элементе гидроаппарата // Вестник Национального технического университета ”Харьковский политехнический институт”. Харьков: НТУ “ХПИ” – №15. – 2001. – С. 127–135.

8. Попов Д.Н. Динамика и регулирование гидро - и пневмосистем. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1987. – 464 с.

9. Попов Е. П., Пальтов И. П. Приближенные методы исследования нелинейных автоматических систем. М.: Гос. изд. физ. мат. лит., 1960. – 792 с.

10. Хохлов В. А. Электрогидравлический следящий привод. – М.: Наука, 1964. – 231 с.

11. Андренко П.Н., Дмитриенко О.В., Асатрян Р.Я. Использование пульсаций давления рабочей жидкости в системах гидроприводов// Вестник Харьковского государственного политехнического университета. – Харьков: ХГПУ. – вып. 7. – ч. 2. – 1997. – С. 35 – 37.

12. Электрогидравлические следящие системы. Хохлов В. А., Прокофьев В. Н. и др. Под ред. В. А. Хохлова. – М.: Машиностроение. 1971, – 431 с.

13. Данилов Ю.А., Кирилловский Ю.Л., Колпаков Ю.Г. Аппаратура объемных гидроприводов: Рабочие процессы и характеристики. – М.: Машиностроение, 1990. – 272 с.

14. Цзе Ф. С., Морзе Н. Е., Хинкл Р. Т. Механические колебания. Перевод с англ. – М.: Машиностроение, 1966. – 508 с.

15. Попов Е. П. Прикладная теория процессов управления в нелинейных системах. – М.: Наука, 1973. – 584 с.