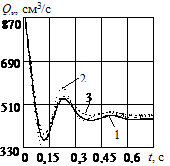УДК 621. 891

 

РОЗРАХУНОК СИЛИ ТЕРТЯ НА ЗАПОРНО-РЕГУЛЮЮЧОМУ ЕЛЕМЕНТІ гідроапарата з вібраційною лінеаризацією

 

З.Я. ЛУР’Є, докт. техн. наук, П.М. Андренко, канд. техн. наук, НТУ "ХПІ", м. Харків.

 

Источник: Сборник трудов Сумского государственного университета "Вісник СумДУ", Сумы, 2010г.

 

Приведен обзор аналитических зависимостей для расчета силы трения на запорно-регулирующих элементах гидроаппаратах. Уточнена формула для расчета силы трения на запорно-регулирующем элементе гидроаппарата, выполненного в виде плунжер-гильза. Обосновано ее применение в математических моделях гадроаппаратов с вибрационной линеаризацией.

 

The review of analytical dependences for calculation of force of friction on shutoff-and-regulation elements hydraulic valves is resulted. The formula for calculation of force of friction on a shutoff-and-regulation element of the hydraulic valves executed in the form of a plunger-sleeve is specified. Its application in mathematical models hydraulic valves with vibrating linearisation is proved.

 

Вступ. У світовій і вітчизняній практиці створення гідроапаратури визначилася тенденція використання гідроапаратів (ГА) з вібраційною лінеаризацією. Запорно-регулюючи елементи (ЗРЕ) таких ГА здійснюють осцилюючий рух з великою частотою і малою амплітудою, усуваючи, таким чином, силу сухого тертя. Вони застосовуються в високодинамічних та високоточних слідкуючих гідроагрегатах, значно покращуючи характеристики останніх. В процесі проектування таких ГА виникає необхідність в докладному визначенню окремих складових їх математичних моделей, в тому числі і сили тертя.

Аналіз публікацій. Одним з основних параметрів пари плунжер-гільза, що визначає її якість, є сила тертя спокою, величина якої для реальної пари залежить від величини тиску в гідроагрегаті, збільшуючись зі збільшенням останнього, а також від правильності геометричних форм плунжеру і гільзи, співвісності їх розташування [1]. Крім цього, на величину сили тертя впливає радіальний зазор у парі плунжер-гільза, матеріал, з якого вони виготовлені, якість їх обробки, форма, фізико-хімічні властивості робочої рідини (РР), що використовується в гідроагрегаті, її температура, а також наявність у ній абразивних часток. Вплив на силу тертя матеріалу і якості його обробки досить докладно розглянуті в роботах [2, 3, 4, 5] та інших. Можливості зменшення за їх рахунок сили тертя, на сьогодні, практично вичерпані, тому далі їх розглядати не варто.

При визначенні сили тертя, яка діє на ЗРЕ ГА, виконаного у вигляді пари плунжер-гільза, більшість дослідників виходили з того, що плунжер в гільзі чи корпусі розташовано ексцентрично, виконано з невеликою конусністю та прямий контакт плунжера з гільзою відсутній [1, 6]. Таке припущення дозволяє отримати точні математичні залежності для визначення сили тертя. Однак, розрахунок сил тертя згідно отриманих залежностей не співпадав з даними, отриманими експериментальним шляхом, що доведено в статті [7]. У відповідності з експериментальними даними, наведеними в цій роботі, встановлено, що дійсне положення плунжера в гільзі, незалежно від його форми, при подачі РР – розташування безпосередньо біля однієї зі стінок.

Більшість дослідників [8, 9, 10] та інші, при розрахунках сили тертя в пристроях гідроагрегатів, в тому числі й ГА, визначають її з залежності:

,                                                   (1)

де  – час;  – сила сухого тертя;  – переміщення ЗРЕ; – функція Кронекера.

У загальному випадку, точне визначення сили  є неможливе. Вона може бути визначена, з достатнім ступенем наближення, якщо відомі умови роботи ГА, точні геометричні виміри і форма ЗРЕ, матеріал пари тертя, якість його обробки та ряд інших факторів. Зазвичай, цю силу для конкретного ГА визначають експериментальним шляхом.

У роботі [2] силу тертя в ГА пропонується розраховувати за залежністю:

,                                                        (2)

де  – коефіцієнт тертя, що в попередніх розрахунках приймають рівним 0,1 – 0,2 [2];  – радіальний тиск, що визначають у залежності від тиску в гідравлічній системі, за таблицями, наведеними у роботі [2];  – діаметр ЗРЕ;  – висота ущільнення.

Розрахувати силу тертя за формулою (2) можна лише приблизно, оскільки заздалегідь невідомо точне значення радіального тиску . Отже, використання формули (2) для розрахунку сили тертя обмежено.

Розглядаючи сили, що діють на золотники ГР, у роботі [11], силу тертя пропонується розраховувати за формулою:

 ,                                                       (3)

де  – коефіцієнт тертя, що у роботі [11] визначений на підставі проведених експериментів;  – поперечна сила, що діє на золотник ГР і виникає внаслідок погрішностей виготовлення, несиметричності розподілу тиску уздовж щілини та розраховується за залежністю [11]

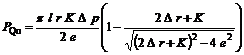,                   (4)

де  – довжина поверхонь тертя;  – радіус втулки поршня золотника;  – конусність поршня золотника на довжині перекриття;  – перепад тиску, що діє на бічні поверхні золотника, який визначається на підставі експериментальних даних; e – ексцентриситет поршня золотника щодо втулки;  – радіальний зазор між поршнем і втулкою золотника.

Розрахунок сили тертя за формулою (4), також викликає певні труднощі, зв'язані з необхідністю знання значень коефіцієнта тертя і перепаду тиску, що діє на бічні поверхні золотника. Отже, і використання формули (4) для розрахунку сили тертя обмежено.

У статті [12] силу тертя розраховують згідно залежності:

_{,                                 (5)}

де  и  – відповідно сила тертя при знаходженні рухомого елемента в стані спокою та при його русі.

У статті [13] силу тертя пропонується розраховувати за залежністю:

,                        (6)

де  – сила контактного тертя;  – дельта функція Кронекера.

В [13] сила тертя спокою  визначена експериментально, для конкретного ГА, що істотно обмежує область застосування формули (6).

У роботі [14] силу контактного тертя в ГА пропонується розраховувати за залежністю:

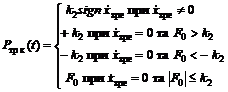,                                       (7)

де  і  знаходяться з рівняння

,                                                   (8)

де m – маса ЗРЕ та пов’язаних з ним частин.

Залежність (7) точно визначає силу контактного тертя на рухливих елементах ГА. Однак її використання на попередніх етапах проектування ГА ускладнено, тому що в загальному випадку не завжди відомі конструктивні параметри ГА необхідні для розрахунку сили , що входить до рівняння (8).

Ряд дослідників зневажають силою сухого тертя і розглядають силу тертя як силу рідинного тертя, яку розраховують згідно залежності [15]:

                                                      ,                                              (9)                                                        

де  – коефіцієнт тертя.

Це дозволяє значно спростити рівняння руху рухомих елементів пристроїв, яке входить до математичних моделей, згідно яких визначають динамічні характеристики цих пристроїв, однак може бути використане лише як розв’язок першого наближення.

Залежності (1) – (9) носять загальний характер. Точність розрахунку, згідно з ними, сили тертя визначається точністю розрахунку їх окремих складових.

В роботі [16] силу тертя в ГА розглядають як суму сил: сили тертя, породжуваної зрушенням шарів рідини в зазорах пари тертя, в умовах її перекосу – , і сили сухого (контактного) тертя –  у зонах контакту ЗРЕ і гільзи.

 =+.                                                 (10)

При цьому, силу сухого тертя, коли швидкість руху ЗРЕ не перевищує критичної – 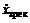, розраховують згідно залежності, яка враховує ексцентричне розміщення ЗРЕ в гільзі:

 = 2,                                          (11)

де  – коефіцієнт тертя, значення якого мало змінюється і знаходиться в межах 0,19 – 0,21;  – радіальна сила, що діє на ЗРЕ та розраховується згідно залежності:

 = ,                                                  (12)

де  – сила пружини;  – зсув пружини;  – загальна довжина ЗРЕ.

Значення  розраховували за формулою [16]:

 =,                                             (13)

де ,  – коефіцієнт кінематичної в’язкості РР () – коефіцієнт, що характеризує положення ЗРЕ в гільзі;  – коефіцієнт динамічної в’язкості РР; =  – коефіцієнт тертя [16]; – радіальний зазор.

Розрахована, згідно залежностей (11) і (12), сила сухого тертя не враховує дійсне розміщення ЗРЕ в гільзі (радіальний зазор, зсув контактних витків пружини), що знижує точність розрахунків, а отже, потребує уточнення. Крім того, формула, наведена в [16], не зовсім коректна, так як містить розмірний коефіцієнт.

В останніх публікаціях [13, 17] силу тертя розраховують згідно залежності:

,                                          (14)

яка враховує як силу сухого – , так і силу рідинного тертя – , відображає фізику процесу та правомірно може бути використана в подальших розрахунках. Слід відзначити, що, як і більшість дослідників, при визначенні сили тертя автори робіт [13, 17] використовували коефіцієнти, отримані експериментальним шляхом, що накладає певні обмеження на область використання отриманих результатів.

В роботі [18] силу рідинного тертя розраховують за залежністю:

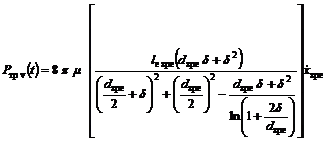,      (15)       

де  – ефективна довжина контакту між ЗРЕ і гільзою.

Однак, формула (15), хоч и враховує розміри пари тертя, не враховує дійсне розміщення ЗРЕ в гільзі, а отже також потребує уточнення.

Таким чином, для розрахунку сили тертя ЗРЕ в гільзі правомірно використовувати залежність (14), яка враховує як силу сухого тертя, так і силу рідинного тертя. При цьому, для визначення складових рівняння (14) можна використати залежності (11), (12) і (15), які повинні враховувати дійсне розміщення ЗРЕ в гільзі, його форму і потребують уточнення.

Ціль і завдання дослідження. Уточнення аналітичної залежності для розрахунку сили тертя на ЗРЕ ГА з вібраційною лінеаризацією, обґрунтування правомірності її використання.

Аналітична залежність для розрахунку сили тертя на ЗРЕ ГА з вібраційною лінеаризацією. При визначені цієї сили вважаємо, що розташування ЗРЕ відносно втулки завжди асиметричне а основним фактором, що визначає таке положення ЗРЕ, є пружина. При русі ЗРЕ сила тертя, з достатньою для практичних розрахунків точністю, може бути описана за допомогою кривої Штрибекка [19], ідеальний вид половини якої показаний на рис. 1. Залежність  в області 0 <  <  неоднозначна, тому що сила тертя при = 0 (сила тертя спокою), залежить від швидкості, при якій ЗРЕ починає рухатися в протилежний бік (рис. 1). Найкращим є випадок, коли рух у протилежний бік почнеться в точці б, тому що при цьому, сила тертя в точці = 0 прагне до свого мінімального значення. Отже, оптимальна швидкість осциляції ЗРЕ ГА повинна дорівнювати . Сила тертя, значною мірою, залежить від ексцентриситету пружини, який залежить від її розміщення в ГА, та може бути визначений з залежності [20]:

,                          (16)

де – середній діаметр пружини;  – число робочих витків пружини.

 

 

Розрахунок сили тертя будемо проводити, використовуючи залежність (14). Уточнимо окремі її складові. Вважаємо, що ЗРЕ займає асиметричне положення і має точки контакту з гільзою, а кут перекосу зневажливо малий. Використовуючи залежність (16), радіальну силу розраховуємо згідно залежності:

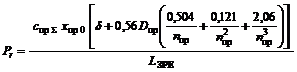,                   (17)

де с_прΣ – сумарна жорсткість пружини;  – попередній підтиск пружини.

Тоді, залежність для розрахунку сили сухого тертя (11) може бути записана у вигляді:

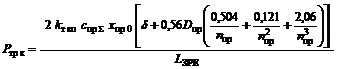.          (18)

Уточнимо також залежність для розрахунку сили рідинного тертя (15), в яку підставимо коефіцієнт – , який враховує положення ЗРЕ в гільзі, і розраховується за уточненою нами залежністю з роботи [16]:

,

де  – відносний коефіцієнт кінематичної в’язкості РР, .Враховуючи цей коефіцієнт, залежність для розрахунку сили рідинного тертя матиме вигляд:

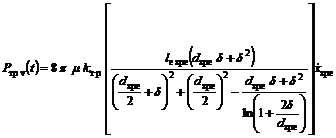.          ₍₁₉₎

Підставляючи в (14), (18) і (19) отримали уточнену нами залежність для розрахунку сили тертя ЗРЕ ГА з вібраційною лінеаризацією:

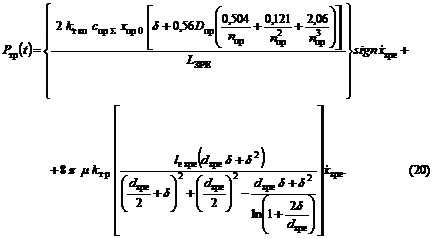
Відзначимо, що знаючи значення критичної швидкості руху ЗРЕ (залежність (13)), можемо визначити характер процесу тертя. Якщо при максимальній швидкості руху ЗРЕ змащування рідинне, то його зворотно-поступальній рух починається в умовах змішаного змащування, а в середині полуперіоду відбувається перехід до рідинного змащування. Зміна сили тертя відбувається так, як показано на рис. 1 пунктирною лінією.

Обґрунтування правомірності застосування уточненої залежності для розрахунку сили тертя на ЗРЕ ГА з ГВК у їх математичних моделях.  З появою пакетів прикладних програм, з'явилася можливість одержання характеристик ГА та інших гідравлічних пристроїв, шляхом розв’язку нелінійних рівнянь, які описують процеси, що відбуваються в них. У таких математичних моделях, для розрахунку сили тертя, можуть бути використані формули (6) і (7), що більш повно відповідають фізиці процесу тертя.

Для правомірності використання уточненої нами формули, для розрахунку сили тертя, в математичних моделях ГА з вібраційною лінеаризацією провели порівняльну оцінку близькості отриманих рішень з використанням різних залежностей для розрахунку сили тертя. Порівняння проводили за допомогою графіків перехідних процесів у гідроагрегаті з клапаном прямої дії з ГВК, отриманих в пакеті прикладних програм, математична модель якого наведена в статті [21].

Для оцінки близькості перехідних процесів клапана використовували відносну інтегральну оцінку:

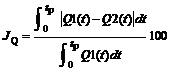%,                                      (21)

де, як приклад, взяли  і  – відповідно витрати через клапан, розраховані з використанням уточненої нами залежності для розрахунку сили тертя (20) і згідно залежностей з літератури;  – час перехідного процесу.

Оцінка (21) характеризує відношення значень різних площ під кривими і  до площі під кривою  за час перехідного процесу . Проведені попередні розрахунки перехідних процесів клапана показали, що с. Для розрахунку відносної інтегральної оцінки приймали с.

Характер перехідних процесів зміни сили тертя на ЗРЕ клапана, витрати через нього і тиску в гідроагрегаті, розраховані з використанням різних залежностей для розрахунку сили тертя показали досить гарний збіг (рис. 3).

 

 

 

 

Рис. 3. Графіки перехідних процесів клапана, розраховані з використанням різних залежностей для розрахунку сили тертя, при  = 901 , : а – сили тертя; б – витрати на виході клапана; в – тиску в гідроагрегаті; 1 – уточнена залежність; 2 – формула (6) [13]; 3 – формула (7) [14]

 

 

Таблиця

Результати розрахунку відносної інтегральної оцінки сили тертя на ЗРЕ клапана з вібраційною лінеаризацією, витрати через нього і тиску в гідроагрегаті, розраховані з використанням різних залежностей для розрахунку сили тертя,  = 901 , f = 200 Гц

 

 

Максимальне значення відносної інтегральної оцінки сили тертя (табл.), отримане при використанні для її розрахунку формули (7). Однак, відносна інтегральна оцінка витрати через клапан і тиску в гідроагрегаті, відповідно, складають 6,4 % і 1,42 %. Це дозволяє стверджувати, що використання, для розрахунку сили тертя в ГА з вібраційною лінеаризацією, уточненої нами залежності є цілком обґрунтованим.

Висновки.  Уточнена аналітична залежність для розрахунку сили тертя ЗРЕ ГА з вібраційною лінеаризацією, при його зворотно-поступальному русі, яка, крім параметрів осциляції його ЗРЕ, враховує його розташування в гільзі та конструктивні параметри пари тертя. Обґрунтовано правомірність її застосування в математичних моделях ГА з вібраційною лінеаризацією.

 

Список літератури: 1. Башта Т.М. Гидравлические приводы летательных аппаратов. – М.: Машиностроение, 1967. – 495 с. 2. Абрамов Е.И., Колисниченко К.А., Маслов В.Т. Элементы гидропривода. Справочник. – К.: Техника, 1977. – 320 с. 3. Войтов В.А., Лурье З.Я., Жерняк А.И. Масштабный фактор пары трения и его учет на этапе проектирования гидромашин // Вестник машиностроения. – № 6, 1995. – С. 15 – 18. 4. Подшипники скольжения / Н. Типей, В.Н. Константинеску, А.Л. Ника, О. Бицэ, – Бухарест: Академия РСН, 1964. – 457 с. 5. Проектирование гидростатических подшипников / Под ред. Г. Риппела. Пер. с англ. – М.: Машиностроение, 1967. – 136 с. 6. Навроцкий К.Л. Теория и проектирование гидро- и пневмоприводов. – М.: Машиностроение, 1991. –384 с. 7. Gwiazda I.B., Gwiazda A.S. Przyczyny zakleszczania cylindrycznych rozdzielaczy hydraulicznych.// Maszyny gornicze. – № 3\74 – Gliwice, wresien 1998, – s. 25–34. 8. Гамынин Н.С. Гидравлический привод систем управления. – М.: Машиностроение, 1972. – 376 с. 9. Коробочкин Б.Л. Динамика гидравлических систем станков. – М.: Машиностроение, 1976. – 240 с. 10. Машиностроительный гидропривод. Л.А. Кондаков, Г.А. Никитин, и др. Под ред. В.Н. Прокофьева. – М.: Машиностроение, 1978. – 495 с. 11. Wanner K. Messung und Unterssuchung der axielen Krufte an olhydraulishen Stenershibern Tecnische. – Hochschule, 1960. – 123 s. 12. Шамберов В.Н. Фрикционные колебания в гидравлических системах// Гидравлика и Пневматика. Информ.-техн. журнал. – Санк-Петербург, 2005. – №21. – С. 15 – 17. 13. Korzeneniowski R., Pluta J. Identyfikacja sil tarcia w serwonapedzie elektropneumatycznym // International scientific-technical conference HYDRAULIC AND PNEUMATICS ’2005. – Wroclaw, 2005. – P. 283 – 292. 14. Скляревский О.М. Об’ємний гідропривід: Навчальний посібник Запоріжжя: ЗНТУ. 2001. – 212 с. 15. Машиностроительный гидропривод. Л.А. Кондаков, Г.А. Никитин, и др. Под ред. В.Н. Прокофьева. – М.: Машиностроение, 1978. – 495 с. 16. Данилов Ю.А., Кирилловский Ю.Л., Колпаков Ю.Г. Аппаратура объемных гидроприводов: Рабочие процессы и характеристики. – М.: Машиностроение, 1990. – 272 с. 17. Зайончковський Г.Й. Оцінка стійкості і протифлатерних властивостей гідромеханічних рульових слідкуючих приводів // Промислова гідравліка і пневматика. – Віниця: ВДАУ, 2006. – №1 (11). – С. 53 – 58. 18. Красов Н.М. Гидравлические элементы в системах управления. – М.: Машиностроение, 1967. – 255 с. 19. Mednis W. Využitie brumového singnálu v prevádzkových jednotkach proporcionálnej techniki. // Hydraulika a pneumatyka 2/2000, – S. 25 – 27. 20. Хвингия М.В., Богданова А.М., Габарадзе Д.Т. и др. Колебания и устойчивость упругих систем машин и поборов. – Тбилиси: Мецниереба, 1974. – 284 с. 21. Лур’є З.Я., Андренко П.М. Обґрунтування правомірності дослідження характеристик гідроапаратів з гідравлічним вібраційним контуром по їх лінеарізованим математичним моделям // Східно-Європейський журнал передових технологій. – Харків, 2006. – № 6/3 (24). – С. 15 – 19.

 

Поступила до редколегії 12.09.07