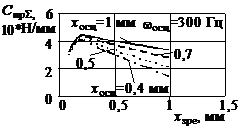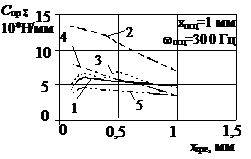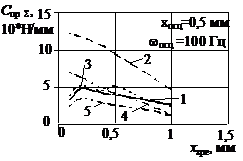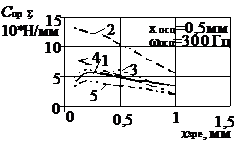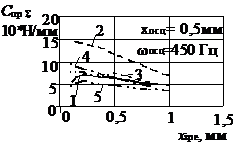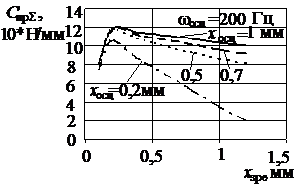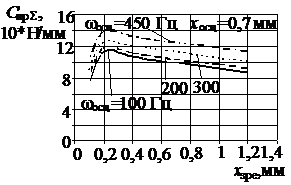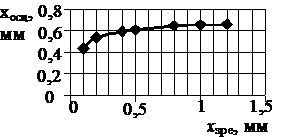УДК 621 – 52

 

ВИБІР СУМАРНОЇ ЖОРСТКОСТІ ПРУЖИНИ ГІДРОАПАРАТІВ ІЗ ГІДРАВЛІЧНИМ ВІБРАЦІЙНИМ КОНТУРОМ

 

Андренко П. М., канд. техн. наук, Гречка І. П. Національний технічний університет “Харківський політехнічний інститут”

 

Источник: Сборник трудов Национального технического университета «ХПИ» «Весник ХПИ», Харьков, 2010г.

 

Определено влияние перемещения запорно-регулирующего элемента гидрораспределителей с гидравлическим вибрационным контуром и новым гидравлическим вибрационным контуром, на изменение суммарной жесткости пружины этого контура. Приведены рекомендации по ее рациональному выбору, а также выбору параметров осцилляции и формы дросселирующей щели запорно-регулирующего элемента.

 

Influence of moving of a locking-regulating element of hydroallocators with a hydraulic vibrating contour and a new hydraulic vibrating contour, on change of total rigidity of a spring of this contour is determined. Recommendations at its rational choice, and also a choice of parameters oscillation and forms throttling cracks of a locking-regulating element are resulted.

 

Вступ

Одним з ефективних способів покращення динамічних характеристик гідроапаратів (ГА) є використання в них вібраційної лінеаризації. Певний клас таких апаратів становлять ГА з гідравлічним вібраційним контуром (ГВК), і ГА з новим гідравлічним вібраційним контуром (НГВК). Характеристики таких ГА значною мірою залежать від параметрів осциляції їх запорно-регулюючих елементів (ЗРЕ), які, в свою чергу, залежать від сумарної жорсткості пружини ГВК чи НГВК.

 

Аналіз публікацій

Питанням проектування ГА, у яких вібраційна лінеаризація здійснюється електричним вібраційним контуром, присвячена досить велика кількість наукових робіт [1 – 3 та ін.]. Зокрема, в [1] наведено методику проектування таких ГА, з урахуванням конструктивних та робочих параметрів гідроагрегату. Визначені межі зміни параметрів осциляції їх ЗРЕ, при яких не втрачається стійкість виконавчих механізмів та не відбувається розірвання робочої рідини (РР). Однак, в цих роботах відсутній аналіз, щодо впливу параметрів осциляції ЗРЕ на характеристики ГА та гідроагрегату, зокрема на точність регулювання.

В [2] наведені границі зміни амплітуди осциляції ЗРЕ ГА, в межах яких забезпечується стійка робота гідроагрегату, проаналізовано вплив конструктивних параметрів виконавчого механізму на стійкість гідроагрегату. Встановлено, що значення коефіцієнта витрат ГА у робочому діапазоні переміщень його ЗРЕ повинно бути максимальним, а ефективна довжина робочих кромок ЗРЕ – невеликою. Однак, в цій роботі, не наведено аналізу, щодо впливу зміни амплітуди осциляції ЗРЕ на вихідні характеристики гідроагрегату.

Більш повно це питання знайшло висвітлення в [3], де наведені залежності, які дозволяють провести попередній вибір параметрів осциляції ЗРЕ ГА з електричним вібраційним контуром. В цій же роботі відмічено, що зі зміною параметрів гідроагрегату відбувається й зміна параметрів осциляції ЗРЕ ГА, що викликає зміну характеристик, як ГА, так і гідроагрегату в цілому, і, в цьому випадку, параметри осциляції ЗРЕ ГА необхідно весь час підстроювати. Зауважимо, що величина коефіцієнта підсилення нелінійної ланки, якою є ГА, по-перше залежить від параметрів осциляції ЗРЕ, в першу чергу, від амплітуди осциляції ЗРЕ, по-друге від форми нелінійності (величини перекриття та форми дроселюючої кромки), і в-третє, від структури та параметрів системи в цілому. Від цих чинників, в тому числі й від зовнішніх перешкод, буде залежати й границя стійкості системи.

Спроба вирішення цієї задачі, щодо ГА з ГВК, зроблена у [4]. Розглядаючи лінійну математичну модель ГА, в ній встановлено, що найбільший вплив на амплітуду осциляції ЗРЕ має сумарна жорсткість пружин та амплітуда пульсацій тиску в камері керування. Однак, наведена в даній статті математична модель не враховує нелінійність та гідродинамічну силу, а також форму дроселюючої кромки ЗРЕ.

В [5] наведені результати розрахункових досліджень параметрів осциляції ЗРЕ ГА з ГВК та НГВК, які отримані на підставі розгляду нелінійної математичної моделі з урахуванням тертя та третьої гармоніки процесу осциляції. Результати досліджень, наведені в ній співпадають з результатами [4], а чисельні дані є більш точними. Однак в цій роботі також не враховано змінність гідродинамічної сили, та форму дроселюючої кромки ЗРЕ, відсутній аналіз зміни параметрів осциляції ЗРЕ, при зміні його переміщення. Отже, визначення впливу параметрів осциляції ЗРЕ ГА з ГВК та НГВК, на зміну сумарної жорсткості пружини, та її раціональний вибір, є актуальною науково-технічною задачею.

 

Дроселюючі кромки ЗРЕ ГА

Застосування в ГА дроселюючих кромок різної форми дозволяє отримувати, по-перше, будь-які бажані закони зміни площі дроселюючої щілини від переміщення його ЗРЕ, а, по-друге, при вибраному законі зміни площі дроселюючої щілини, змінювати робочий діапазон переміщень ЗРЕ. Стосовно ГА, у яких ЗРЕ виконаний у вигляді прецизійної пари плунжер-гільза, різноманітні їх форми та залежності для визначення площ та витрат наведені в [6]. Як найбільш розповсюдженні, будемо розглядати наступні форми дроселюючих кромок: тип – I, гостра дроселююча кромка; тип – II, конічна дроселююча кромка; тип – III, дроселююча кромка з трикутними запилками; тип – IV, дроселююча кромка з запилками у вигляді сегмента круга; тип – V, дроселююча кромка гостра з напівкруглою канавкою.

 

Теоретичне визначення сумарної жорсткості пружини

Для ГА з ГВК чи НГВК сумарна жорсткість пружин ГА –  при сталому сигналі керування, без урахування жорсткості, викликаної її попередньою деформацією та постійною амплітудою осциляції ЗРЕ, може бути визначена з залежності [7]:

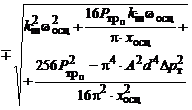,          (1)

де ,  – відповідно коефіцієнти жорсткості гідродинамічної та рідинної пружини;  – маса ЗРЕ та пов’язаних з ним рухомих частин, у тому числі й 1/3 маси пружини;  – коефіцієнт, який враховує інерційну дію несталого потоку на ЗРЕ;  – сила тертя спокою; ,  – відповідно частота і амплітуда осциляції; А – амплітуда пульсацій в процентах від тиску живлення;  - діаметр торців рухомих частин ЗРЕ з боку камер ГВК;  – перепад тиску в камерах керування ГВК.

Залежність (1) характеризує зміну сумарної жорсткості пружин ГА з ГВК в залежності від змінної гідродинамічної сили, жорсткості рідинної пружини, маси ЗРЕ, амплітуди та частоти її осциляції. Визначимо величини, що входять до (1). Коефіцієнти осьової складової гідродинамічної сили визначаються за відомими залежностями:

,               (2)

,       (3)

де  – коефіцієнт витрат ГА, який визначали по [6];  – ширина вікон втулки ГА;  і  – відповідно тиски живлення та зливу;  – кут нахилу вектора швидкості потоку РР до осі ЗРЕ;  – щільність РР;  і  – відповідно відстані між осями каналів зливу і живлення та дроселюючою кромкою ЗРЕ.

Кут нахилу вектора швидкості потоку РР до осі ЗРЕ значною мірою залежить від типу дроселюючої кромки ЗРЕ. Його визначення за результатами розрахунків, проведених в [8], дозволило встановити, що він становить для ЗРЕ тип I – 69; тип II – 43; тип III – 53; тип IV – 63; тип V – 75.

 – середній коефіцієнт жорсткості рідинної пружини, який при умові великого відносного об'єму трубопроводів та каналів , що, зазвичай, має місце в ГВК та НГВК, визначається з залежності [1]:

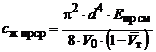,            (4)

де Е_{пр см} – приведений модуль об'ємної пружності РР, з урахуванням нерозчиненого повітря, та пружності стінок трубопроводу; V₀ – об'єм РР, що знаходиться в кожній камері керування при середньому положенні ЗРЕ;  – відносний об'єм трубопроводів та камер керування: , де V_т – об'єм трубопроводів. Якщо прийняти, що камери керування ГА та трубопроводи з обох сторін ГА рівні, то жорсткістю рідинної пружини можна знехтувати.

Сила тертя спокою визначається, в основному, силою контактного тертя й може бути приблизно обчислена за залежністю [6]:

 =2,                (5)

де  – коефіцієнт тертя, значення якого мало змінюється, і дорівнює 0,19–0,21;  – радіальна сила, що діє на ЗРЕ, і може бути отримана з розгляду його перекидаючого моменту в гільзі, обумовленим несиметричним додатком сили пружини. З огляду на те, що кут перекосу ЗРЕ малий, можемо записати:

 =,                           (6)

де L – загальна довжина золотника;  – сила пружини;  – зсув пружини, який визначаємо по Валю

,      (7)

де  – число робочих витків пружини;  – середній діаметр пружини.

Підставляючи в (5), значення з (6) і (7), одержимо:

.  (8)

 

Врахування параметрів осциляції ЗРЕ в математичних моделях ГА з ГВК та НГВК. Відповідно з методикою вібраційної лінеаризації, процеси, що відбуваються в ГА з ГВК та НГВК, можуть бути розраховані за лінійним рівнянням, до якого входить k_н – коефіцієнт підсилення, який, у загальному випадку, залежить не тільки від структури та параметрів ГА, але й від амплітуди та частоти зовнішньої сили та, в загальному випадку, визначається з залежності:

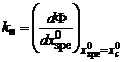,                 (9)

де Ф – функція зсуву;  – переміщення ЗРЕ ГА; х_с⁰ – номінальне значення , яке задається умовами конкретної задачі, та, як було відмічено вище, залежить від положення ЗРЕ.

Зауважимо, що сила тертя спокою для ідеальної релейної характеристики входить до функції зсуву. Тобто, коефіцієнт підсилення залежить від сили пружини (сумарної), яка змінюється при переміщені ЗРЕ, і залежить від її жорсткості. Для отримання стабільних характеристик ГА з ГВК зміна сумарної жорсткості його пружин вздовж переміщення його ЗРЕ, яка обумовлена зміною гідродинамічної сили, жорсткості рідинної пружини, амплітуди та частоти її осциляції ЗРЕ, та його маси, повинна бути незначною [7].

 

Розрахункові дослідження зміни сумарної жорсткості пружини

Їх проводили у пакеті прикладних програм. Розглядали наступні ГР: ГР з ГВК, діаметр ЗРЕ та діаметр його поршня 10 мм, загальна довжина ЗРЕ 30 мм, максимальний його хід 1 мм, а маса 0,13 кг, жорсткість пружини 90 Н/мм, тиск живлення 6,3 МПа; ГР з НГВК, діаметр золотника 16 мм, діаметр його поршня 12 мм, загальна довжина золотника 35 мм, максимальний хід золотника 1,2 мм, а маса 0,186 кг, жорсткість пружини 120 Н/мм, тиск живлення 12,0 МПа. Тиск зливу в обох випадках дорівнював атмосферному, а тиск навантаження дорівнював половині тиску живлення. Вважали, що амплітуда пульсацій тиску на виході об’ємної гідромашини складала 3% від тиску живлення.

В залежності від перепаду тиску на торцях ЗРЕ визначали його переміщення, коефіцієнти жорсткості гідродинамічної та рідинної пружини, коефіцієнт, який враховує інерційну дію несталого потоку на ЗРЕ, силу тертя спокою, коефіцієнт витрат. Приймали, що частота та амплітуда осциляції є постійними.

Результати розрахунків наведені на рис. 1, 2. При переміщенні ЗРЕ характер зміни сумарної жорсткості пружини ГВК, для визначеного типу ЗРЕ, не залежить від зміни частоти його осциляції (рис.1 а, б, 2 а, б). Аналіз впливу типу дроселюючої кромки ЗРЕ (рис. 1в, г) на сумарну жорсткість пружини дозволив встановити, що в ГР з ЗРЕ типів V та I зміна сумарної жорсткості пружини при переміщені ЗРЕ – найменша. Отже, й найменший вплив переміщення ЗРЕ (при умові, що частота осциляції постійна) на амплітуду його осциляції. Причому, із збільшенням частоти та амплітуди осциляції відносне відхилення сумарної жорсткості пружини від її середнього значення зменшується. Цей висновок відповідає сучасній тенденції розвитку ГА з вібраційною лінеаризацією на збільшення частоти осциляції ЗРЕ.

 

Рис. 1. Зміна сумарної жорсткості пружини ГР з ГВК в залежності від переміщення його ЗРЕ: а, б – для ЗРЕ типу V (а – при зміні амплітуди осциляції; б – при зміні частоти осциляції); в, г, д, е – для різних типів ЗРЕ (номер кривої відповідає типу ЗРЕ)

 

Найбільший вплив на сумарну жорсткість пружини спостерігається у ГР з ЗРЕ типу II. Для ГР з ЗРЕ всіх типів найбільший вплив на сумарну жорсткість пружини має амплітуда осциляції. Причому її вплив збільшується з відкриттям ЗРЕ. Так, при збільшенні амплітуди осциляції в два рази зменшується різниця між максимальним та мінімальним значенням сумарної жорсткості пружини. Вплив частоти осциляції на сумарну жорсткість пружини менший. Це пояснюється зміною осьової гідродинамічної сили вздовж переміщення ЗРЕ.

Слід однак зауважити, що значне збільшення амплітуди осциляції ЗРЕ може привести до зменшення витрати через ГР, що є небажаним.

Як видно з рис. 3, при постійній сумарній жорсткості пружини НГВК, при переміщенні ЗРЕ ГР амплітуда його осциляції значно змінюється. Причому на початку відкриття дроселюючої щілини амплітуда осциляції ЗРЕ змінюється більш інтенсивно. Це пояснюється більшою інтенсивністю зміни осьової гідродинамічної сили. Таким чином, підвищення вихідних характеристик ГР з НГВК лежить, перед усім, в площині забезпечення стабільної амплітуди осциляції його ЗРЕ. Це може бути досягнуто шляхом використання пружин НГВК із змінною жорсткістю.

Використання фасонних пружин, які мають нелінійні пружні характеристики, дозволить компенсувати зміну осьової гідродинамічної сили, отримати стабільну амплітуду осциляції ЗРЕ. Необхідно також зауважити, що при відповідному конструктивному виконанні така пружина має мінімальні габаритні розміри.

 

Рис. 2 Зміна сумарної жорсткості пружини ГР з НГВК в залежності від переміщення його ЗРЕ: а – при зміні амплітуди осциляції; б – при зміні частоти осциляції

 

Рис. 3 Зміна амплітуди осциляції ЗРЕ ГР з НГВК в залежності від переміщення його ЗРЕ

 

Висновки

Вперше визначено вплив переміщення ЗРЕ ГР з ГВК та НГВК на зміну сумарної жорсткості пружини цього контуру. При визначені сумарної жорсткості пружини враховувалися амплітуда та частота осциляції ЗРЕ, форма його дроселюючої кромки, змінність коефіцієнтів витрат та кут нахилу вектора потоку РР до осі ЗРЕ.

Розрахунковим шляхом встановлено, що для забезпечення стабільної сумарної жорсткості пружини ГВК та НГВК, амплітуду та частоту осциляції його ЗРЕ треба вибирати, виходячи з їх максимальних значень.

Мало змінне значення сумарної жорсткості пружини ГВК та НГВК дозволить отримати стабільний, у всьому діапазоні переміщень ЗРЕ, коефіцієнт підсилення ГР, завдяки чому збільшиться їх точність. Для чого пропонується використовувати в ГВК та НГВК фасонні пружини, які мають нелінійні пружні характеристики.

 

Список літератури

1. Электрогидравлические следящие системы. Хохлов В. А., Прокофьев В. Н., Борисова Н. А. и др. Под ред. В. А. Хохлова – М.: Машиностроение, 1971. – 431 с.

2. Баранов В. Н., Захаров Ю. Е. Электрогидравлические и гидравлические вибрационные механизмы. – М.: Машиностроение, 1966. – 243 с.

3. Меднис В. Выбор параметров осцилляции золотника пропорциональных гидравлических аппаратов // Вестник НТУ «ХПИ». Харьков: НТУ «ХПИ» – 2001 Вып. 129 Ч.1 – с. 120 – 124.

4. Андренко П. Н. Выбор параметров осцилляции запорно-регулирующего элемента гидроаппарата с гидравлическим вибрационным контуром // Вісник Сумського державного університету. Суми: СумДУ – 2003 – № 13(59). С. 31 – 38.

5. Андренко П. М., Гречка І. П. Розрахункові дослідження параметрів осциляції гідро розподільника з гідравлічним вібраційним контуром // Промислова гідравліка і пневматика. – Вінниця: ВДАУ. – 2005. № 1 (7). – С. 68 – 74.

6. Данилов Ю.А., Кирилловский Ю.Л., Колпаков Ю.Г. Аппаратура объемных гидроприводов. – М.: Машиностроение, 1990. – 272 с.

7. Андренко П. М. Проектування пружин гідроапаратів з гідравлічним вібраційним контуром // Вестник Харьковского Национального автомобильно-дорожного университета. Харьков: ХНАДУ. – Вып.27. – 2004. – С. 125 – 129.

8. Андренко П. М. Визначення кута нахилу вектора швидкості потоку, для розрахунку гідродинамічної сили запорно-регулюючого елементу гідроапарата // Східно-Європейський журнал передових технологій. – Харків. – 2005 – №4/2 (16) – с. 60 – 63.