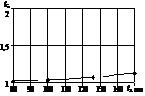УДК 621.55

   Побудова математичної моделі нового гідравлічного вібраційного контуру

 

     П. М. Андренко, канд. техн. наук; І. П. Гречка

 

Источник: Сборник трудов Национального технического университета «ХПИ» «Весник ХПИ», Харьков, 2007г.

        

В статье приведен пример построения нового гидравличесекого вибрационного контура и его математическая модель. Проанализирована правомерность исследования статических и динамических характеристик гидроппарата с новым гидравлическим вибрационным контуром по их линейным математическим моделям. Это позволит использовать математические модели для устранения гистерезиса в гидроаппарата современных систем.

 

           Вступ

Одним із напрямків підвищення характеристик гідроагрегатів та обладнання, збудованого з їх використанням, є застосування в них гідроапаратів із гідравлічним вібраційним контуром та новим гідравлічним вібраційним контуром (НГВК). Схемні рішення таких гідроапаратів вперше наведені в [1], а стосовно гідророзподільника із НГВК ‑ [2]. Як основний елемент НГВК використовується резонатор із відгалуженням (РВ), який до цього використовувався як гасник. У зв’язку з цим постає питання більш докладного дослідження його характеристик, та визначення впливу на них його конструктивних і робочих параметрів. Спроба вирішення цього питання зроблена у даній статті.

 

Аналіз публікацій

Методам проектування РВ, який до цього використовувався як гасник, присвячена невелика кількість робіт. Так, в [3, 4] наведено їх принципові схеми та залежності для визначення об’єму камери та розмірів каналів. В [5] наведено методику проектування, яка заснована на електроаналогії, при використанні якої накладається ряд обмежень, пов’язаннях з розмірами РВ та часом проходження нестаціонарних гідродинамічних процесів. Крім того, використання цієї методики потребує проведення попередніх експериментальних досліджень, що значно ускладнює її використання. В [6] наведені математичні моделі РВ, збудовані з використанням методу Ейлера, але в них відсутні рекомендації щодо визначення їх раціональних, конструктивних і робочих параметрів. Крім того, використання даних математичних моделей є досить трудомістким. Більш повне відображення цієї проблеми знайшло в [7], де наведені математичні моделі таких пристроїв, побудованих з використанням перетворень Фур’є, які можуть бути використані при визначені їх раціональних, конструктивних і робочих параметрів. Однак в ній більше уваги приділено гасникам пульсацій тиску. Отже, визначення конструктивних і робочих параметрів РВ на основі проведення всебічних аналітичних досліджень є актуальною науково-технічною задачею.

 

Мета і задачі дослідження

Метою статті є побудова математичної моделі РВ, аналіз впливу його конструктивних і робочих параметрів на коефіцієнт передачі

 

Обґрунтування вибору методу для побудови математичної моделі НГВК

При течії робочої рідини (РР) в НГВК у ньому відбуваються складні гідромеханічні процеси, що належать до нестаціонарного потоку РР зі зміною гідродинамічних величин у просторі та часі. Зупинимося на їх розгляді більш докладно.

Для опису нестаціонарних гідродинамічних процесів, які мають місце в елементах гідроагрегатів, в припущені, що РР є ньютонівською, більшість дослідників використовують методи, які ґрунтуються на розв’язанні рівнянь руху РР, нерозривності та рівняння стану при заданих граничних та початкових умовах. При цьому використовується один із методів їх розв’язання: прямого розв’язку диференціальних рівнянь (класичний метод), суперпозиційний, спектрального аналізу та операторний [8].

У прямому методі для розв’язку диференціальних рівнянь використовують один із методів чисельного інтегрування: Рунге-Кутта, Ейлера чи метод кінцевих різниць з використанням прямокутної сітки [9]. Останнім часом широке застосування для розв’язання задач гідромеханіки знайшов один із прямих способів розв’язання диференціальних рівнянь – метод характеристик, а саме сітковий метод. Цей метод є кращим у цьому класі, і його використання ефективно при розрахунку неусталеної течії РР з нульовими початковими умовами. З використанням цього методу в [10] проведено розрахунок динаміки позиційного слідкуючого гідроприводу з довгими гідроканалами, де диференціювання рівнянь першого порядку здійснюється методом Ейлера. Однак треба зауважити, що використання методу Ейлера не забезпечує достатньо малу похибку при великому кроці . Тому, зазвичай, для розрахунку гідравлічних систем замість методу Ейлера використовують метод Рунге-Кутта другого та четвертого порядків, а ще краще використати неявний метод, наприклад формулу Адамса.

Зауважимо, що в НГВК відбувається рух пульсуючої РР і не існує часу, коли всі швидкості дорівнюють нулю. Це робить використання сіткового методу для математичного опису НГВК мало придатним. Треба однак зауважити, що інколи для вирішення цієї проблеми використовують метод “розрахунку на встановлення”. У цьому випадку спочатку апріорі набувають нулюві початкові умови, і одним із сіткових методів послідовно розраховують підряд декілька циклів. Розрахунок проводиться до того часу, поки результати не зациклюються, тобто відхилення розрахункових значень за період стають нехтувано малі. Отже, такий чисельний метод є досить трудомістким.

В [11] для розв’язання диференціальних рівнянь, які описують нестаціонарний рух РР в гідроагрегаті, використано метод різницевих схем Рунге-Кутта-Фельбера з визначеним кроком дискретизації. Однак наведена математична модель не враховує запізнення імпульсів тиску, в межах ділянки гідроагрегату, що розглядається. При розрахунках це може привести до значних похибок, особливо в системах, які працюють з великою циклічністю, якою і є НГВК.

До недоліків прямих методів досліджень нестаціонарних гідродинамічних процесів слід віднести труднощі, які виникають при складанні вихідних рівнянь, і великий об’єм розрахунків, а також необхідність проведення розрахунку у повному обсязі, навіть при незначній зміні одного із параметрів. Незважаючи на відмічені недоліки прямих методів досліджень нестаціонарних гідродинамічних процесів, більшість дослідників віддають перевагу саме їм.

Суперпозиційний метод полягає у визначенні реакції системи на довільну функцію, якщо відома реакція цієї системи на одиничну функцію чи одиничний імпульс [12]. Однак його використання для опису періодичного руху РР є трудомістким і тому недоцільним.

Операторний метод. До цього методу належить і метод гармонічної лінеаризації, який дозволяє досліджувати нелінійні гідромеханічні процеси в гідроагрегатах та їх елементах за допомогою перетворень Лапласа [13]. Його використання потребує розрахунку коефіцієнтів гармонічної лінеаризації, які визначені в літературних джерелах тільки для обмеженої кількості типових нелінійностей і розрахунок яких для математичного опису нестаціонарних гідромеханічних процесів є складним та трудомістким.

У [14, 15] розрахунок пульсацій тиску за допомогою перетворень Лапласа виконано з використанням так званих функцій-оригіналів з властивостями  при , що не відповідають умові періодичності коливань. Інколи ці перетворення використовують для математичного опису періодичних коливань [16]. В літературних джерелах, присвячених розробленню даного методу, при розгляді тривалих неусталених процесів, при яких тертя приводить до усталеного процесу, користуються формулами для так званого періодичного оригіналу, використання яких є цілком виправданим.

Для математичного опису та аналізу періодичних процесів замість перетворень Лапласа рекомендується використовувати його “періодичний” аналог Фур’є [8]. Цей аналог може бути використаний при математичному описі гідродинамічних процесів в НГВК.

Зауважимо, що математичний опис нестаціонарних гідродинамічних процесів може бути виконаний також із застосуванням електроаналогії [5, 17]. Однак при цьому накладається ряд обмежень, пов’язаних з геометричними вимірами гідроапаратів, часом проходження нестаціонарних гідродинамічних процесів та необхідністю знання акустичного опору проточних частин гідроапарата до проведення розрахунків. Це робить застосування даного методу малоефективним.

Метод спектрального аналізу ґрунтується на виразі вхідного імпульсу елементарними гармонічними коливаннями [1]. Цей метод досить трудомісткий, оскільки приводить до синтезу великої кількості складових. Враховуючи, що характер зміни пульсацій тиску (швидкості) РР у НГВК з достатньою для практичних розрахунків докладністю може бути прийнятим гармонічним, а витрата РР дорівнює нулю (що значно спрощує розв’язання вихідних рівнянь), його використання для математичного опису руху РР в НГВК є цілком виправданим.

Таким чином, для побудови математичної моделі НГВК будемо використовувати метод спектрального аналізу.

 

                                    Принцип дії РВ

Ó öèë³íäðè÷íîìó êîðïóñ³ 3 (ðèñ. 1) (ºìí³ñíèé åëåìåíò) ðîçì³ùåíî öèë³íäðè÷íèé çâóæåíèé ïàòðóáîê 2 (³íåðö³éíèé åëåìåíò), ÿêèé ÷åðåç ïàòðóáîê 1 ï³äêëþ÷åíî äî ìàã³ñòðàë³ æèâëåííÿ (äæåðåëà ïóëüñàö³é òèñêó). Ðåàë³çîâàíî øóíòóâàëüíèé ðåçîíàíñíèé êîíòóð. Ïàòðóáîê 4 ç’ºäíóº Р³ç êàìåðîþ êåðóâàííÿ ã³äðîðîçïîä³ëüíèêà. Ïóëüñàö³¿ òèñêó ÐÐ íàäõîäÿòü â ºìí³ñòü ÷åðåç ïàòðóáêè 1 òà 2. Ó ðàç³ íàÿâíîñò³ çðóøåííÿ ôàç ïóëüñóþ÷îãî ïîòîêó ðîáî÷î¿ ð³äèíè òà âëàñíî¿ ÷àñòîòè ÐÂ, â³äáóâàºòüñÿ ï³äñèëåííÿ ïóëüñàö³é òèñêó, ÿêèé íàäõîäèòü äî êàìåðè êåðóâàííÿ ã³äðîðîçïîä³ëüíèêà. Äîáèðàþ÷è â³äïîâ³äí³ ºìíîñò³, ïåðåòèí òà äîâæèíó çâóæåíîãî ïàòðóáêà 2, ìîæíà îòðèìàòè ð³çí³ êîåô³ö³ºíòè ï³äñèëåííÿ.

Рисунок 1 - Схема РВ: 1 – вхідний трубопровід; 2 – вхідний звужений патрубок; 3 – камера НГВК; 4 – камера гідророзподільника

 

Математична модель НГВК

При складанні математичної моделі НГВК зробимо такі припущення:

– вважаємо, що в НГВК відбуваються усталені гідродинамічні процеси. Не розглядаємо перехідні процеси, пов’язані з різкою зміною параметрів на його вході. Розглядаємо періодичні гідродинамічні процеси, обумовлені пульсацією тиску РР на виході із насоса;

– припустимо, що профіль розподілу швидкості РР по перерізу каналів НГВК сформований;

– вважаємо, що в гідросистемі, а отже і в НГВК, відсутні резонанс, кавітація РР та гідравлічний удар;

– швидкість звуку РР є величиною сталою, значно більшою від її швидкості в гідросистемі;

– температура РР є сталою і знаходиться в діапазоні 50–55˚С. Сталим також є газовміст РР, який враховується при розрахунку модуля об’ємної пружності РР, який беремо сталим і розраховуємо з урахуванням пружних властивостей трубопроводу;

– рівняння нерозривності РР виконується на всіх ділянках гідросистеми;

– масовими силами РР нехтуємо. Зауважимо, що аналогічне припущення беруть більшість дослідників [18, 19];

– РР вважаємо ньютонівською, а течію ізотермічною;

– течія РР одновимірна осесиметрична.

З урахуванням прийнятих припущень, рух РР у гідросистемі може бути описаний за допомогою хвильового рівняння у вигляді системи двох диференціальних рівнянь першого порядку, яку з урахуванням гідравлічного опору трубопроводу можемо записати у вигляді [8]

 

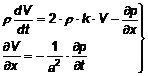, (1)

де ; λ – коефіцієнт гідравлічного опору; d_т – діаметр трубопроводу; ρ – щільність РР; V – швидкість РР; а – швидкість звуку в РР; р – тиск; х – відстань від початку трубопроводу до перерізу, де визначається тиск (швидкість) РР.

Оскільки витрата через НГВК відсутня, членом, який враховує втрати тиску у рівнянні (1), можна знехтувати. Обґрунтування цього припущення наведено в [20].

Розв’язання (1) будемо проводити методом частотного аналізу, а саме методом стоячих хвиль, запропонованим Лутцем для розрахунку хвильових процесів. У відповідності до цього методу, розв’язок (1) може бути записаний в гіперболічній формі [8]

 

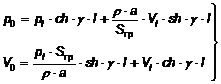, (2)

 

де  – стала поширення хвильового процесу; β – коефіцієнт загасання; φ – хвильове число;  – довжина ділянки трубопроводу (каналу);  – площа поперечного перерізу трубопроводу;  – кругова частота коливань.

Задаючи граничні умови у вигляді повного опору (імпедансу) Z_г і значення амплітуди швидкості та тиску в одному перерізі трубопроводу за допомогою (2), можна знайти значення їх амплітуд у будь-якому іншому перерізі. Причому необхідно також задати граничні умови, що визначаються характером навантаження на кінці трубопроводу. А саме наявність витрати в гідросистемі – дроселі, сопла, насадки та інше. Відсутність витрати – постійні чи змінні об’єми на кінці заглушеного трубопроводу.

Для лінійної ділянки трубопроводу при заданому повному опорі навантаження Z_н і наведеному імпедансі Z₀. Розв’язок (1) може бути записаний у вигляді [21]

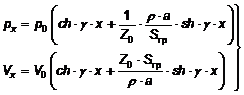, (3)

де для гідросистеми, в якій відсутня витрата РР:

; (4)

. (5)

З урахуванням (4) і (5) рівняння (3) набуде вигляду:

 

. (6)

 

Відмітимо, що (3) дозволяє визначити амплітуди тисків і швидкості в будь-якій точці гідросистеми і для будь-яких типів навантаження.

Для гармонічних коливань при  і  розв’язок (1) можна також записати у вигляді (3) [8], де Z₀ за відсутності внутрішнього тертя визначається із виразу

 

.

 

При розгляді гідродинамічних процесів, що відбуваються в НГВК, хвилі тиску поширюються в його каналах з кінцевою швидкістю, яка значно менша швидкості звуку. Тому зміна параметрів в будь-якій частині НГВК за часом не встигає вплинути на зміну параметрів інших частин. Таке припущення, виходячи із фізичної моделі процесів, що відбуваються в НГВК, відповідає дійсності.

Оскільки всі елементи НГВК являють собою короткі патрубки, вважаємо, що вони всі лінійні, а граничні умови – постійні (на вході в НГВК встановилися гармонічні впливи. При математичному описі гідродинамічних процесів в коротких трубопроводах таке припущення приймається більшістю дослідників і підтверджено численними експериментальними дослідженнями, наприклад [22]. Тоді структурну схему НГВК можна подати у вигляді

 

Рисунок 2 - Структурна схема НГВК: 1 – вхідний трубопровід; 2 – вхідний звужений патрубок; 3 – камера НГВК; 4 – камера гідророзподільника

 

Для розрахунку величини тиску в будь-якому структурному елементі НГВК введемо коефіцієнт передачі, під яким будемо розуміти відношення тиску на вході каналу (патрубка) до його значення на виході:

 

. (7)

 

Таким чином, (7) дозволяє визначити, на скільки збільшиться (зменшиться) величина тиску на виході трубопроводу у порівнянні з його входом. При цьому значення коефіцієнта передачі структурного елемента можемо знайти з першого рівняння (6).

 

, (8)

де .

 

Рівняння (7) може бути використане для розрахунку коефіцієнта передачі пульсацій тиску, тоді замість тиску входу і виходу в нього треба підставити амплітуди пульсацій. Якщо відомі коефіцієнти передачі окремих структурних елементів НГВК і пульсації тиску на його вході, можемо знайти для нього коефіцієнт передачі

 

k_НГВК=k_п1 ^. k_п2 ^. k_п3 ^. k_п4. (9)

 

З рівняння (8) та (9) знайдемо k_НГВК, який після представлення гіперболічних функцій [23], для НГВК, можемо записати у вигляді

 

 (10)

де

.

 

Оскільки в НГВК ω_осц визначається характеристикою джерела живлення (насосом) і в загальному випадку є величиною постійною, рівняння (10) дозволяє, змінюючи довжину патрубка та величину площі його прохідного перерізу, виконати раціональний вибір коефіцієнта передачі НГВК. Відмітимо, що в загальному випадку його величина повинна бути більше 1.

Якщо відомо k_НГВК в припущенні, зміна тиску на виході з насоса відбувається згідно із синусоїдальним законом, можемо знайти пульсації тиску у вихідній камері НГВК:

 

, (11)

 

де  і  – відповідно пульсації тиску в камері НГВК і амплітуда пульсацій тиску на вході в НГВК.

Рівняння (11) є математичною моделлю НГВК. Воно дозволяє визначити силу, що діє на золотник ГР, та параметри його осциляції. Причому вибір d₃ і l₃, виходячи з того, що за фізичною суттю вхідний звужений патрубок і камера 3 НГВК є резонатором Гельмгольца, необхідно робити, використовуючи залежність [8]:

 

, (12)

 

де V₃ – об’єм камери 3 НГВК.

Аналіз залежностей (10) і (12) дозволив встановити, що зі збільшенням довжини камери 3 збільшується і коефіцієнт передачі НГВК. Отже, довжину камери 3 слід вибирати якомога більшою з урахуванням габаритних обмежень НГВК.

 

Розрахункові дослідження впливу параметрів нгвк на його коефіцієнт передачі

У загальному випадку вибір раціонального значення k_НГВК є достатньо трудомісткою задачею, оскільки при ω_осц = const маємо справу з 8 параметрами, які можуть змінюватись самостійно. Введемо обмеження на зміну деяких із них, що дозволить зменшити діапазон їх зміни, завдяки чому зменшується час знаходження їх раціональних значень.

d₁ – діаметр трубопроводу на вході НГВК – за рекомендаціями [24] вибирається таким, що дорівнює або більше D_у ГР. Припустимо, що d₁=D_у ГР;

l₁ – визначається виходячи з місця розміщення гідророзподільника в гідроагрегаті, зазвичай складає 0,3 – 0,5 м. Візьмемо l₁ з цього діапазону;

d₄ дорівнює діаметру поршня d_пор НГВК і його беремо із цих міркувань;

l₄ – вибирається залежно від довжини пружини НГВК.

Дослідження впливу параметрів НГВК на коефіцієнт передачі робили на основі наведеної математичної моделі у пакеті прикладних програм. За базову модель РВ брали розроблену нами, в якій l₃ = 126 мм; d₃ = 32мм; d_у = 10 мм; d₂ = 6 мм; l₂ = 45 мм і яка працює на мінеральному маслі ІГП – 30 при температурі 50С. Змінюючи один із параметрів, визначали коефіцієнт передачі (рис. 3). Як видно з рис. 3, найбільший вплив на коефіцієнт передачі мають діаметри камери і завуженого патрубка. Частота пульсацій РР на коефіцієнт передачі розробленого РВ впливає незначно.

Таким чином, ефективною областю застосування розробленого РВ є діапазон частот 150 – 300 Гц. Зауважимо, що значення k_п > 2, які відповідають умові виникнення в РВ резонансу, є небажані, що треба враховувати при проектуванні РВ.

 

 

                          Висновки

Встановлено, що для побудови математичної моделі НГВК доцільно використовувати метод спектрального аналізу.

З використанням цього методу отримано математичну модель НГВК.

Проведені аналітичні дослідження дозволили встановити, що найбільший вплив на коефіцієнт передачі мають діаметри камери РВ і завуженого патрубка. Для отримання бажаних коефіцієнтів передачі НГВК довжину камери РВ слід вибирати якомога більшою.

 

а	б
в	г
д

Рисунок 3 - Залежність коефіцієнта передачі k_п РВ при зміні:

а – частоти; б – діаметра камери РВ; в – діаметра звуженого патрубка; г – довжини камери РВ; д – довжини звуженого патрубка

 

Список літератури

 

1.     Андренко П. Н. Принцип построения гидравлических аппаратов нового класса //Вестник НТУ “ХПИ”. - 2001.- Вып. 129. - Ч.2. - С. 102 - 106.

2.      Гречка І. П. Математична модель гідророзподільника з НГВК //Автоматизація виробничих процесів. - 2004. - №2 (19). - С. 16 - 23.

3.      Проектирование и изготовление гидроприводов машин с учетом обеспечения минимального шума. – М.: НИИмаш, 1973. – 55 с.

4.      Kollek W., Kudzma Z., Rutanski J. Mozliwosci skutecznego tlumienia halasu ukladem filtrow akustycznych // V Konferencja naukowo-tecniczna: Rozwoj budowy eksploatacji I badan maszyn roboczych ciezkich. Zakopane, 1992. - S. 203 – 208.

5.     Шорин В.П. Устранение колебаний в авиационных трубопроводах. – М.: Машиностроение, 1980. – 156 с.

6.     Андренко П. Н., Клитной В. В., Дмитриенко О. В. Расчет пульсаций давления на выходе однокамерного преобразователя пульсаций // Вестник НТУУ КПИ.-1999. - Том 1. - Вып. 36. - С. 87 – 93.

7.     Андренко П. М., Дмитрієнко О. В. Математичні моделі і розрахункові дослідження гідравлічних гасників і підсилювачів пульсацій тиску // Східноєвропейский журнал передових технологій. – 2004. – № 5 (11). – С. 88 – 93.