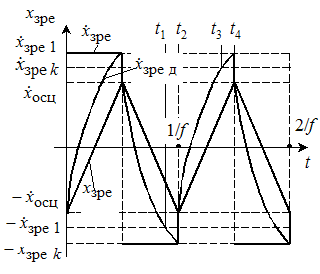УДК 621.11

Визначення сил тертя запірно-регулюючого елемента гідроапаратів з вібраційнною лінеаризаціею.

       Кондратов М.А., магістр, Кононенко А.П., докт. техн. наук, професор, Донецький національний технічний університет.

Источник: Сборник студенческих научных работ ДонНТУ, Донецк, 2010г.

Наведено огляд аналітичних залежностей для розрахунку сил тертя на запірно-регулюючих елементів гідроапаратів. Уточнена формула для розрахунку сил тертя на запірно-регулюючих елементів гідроапаратів, виконаних у вигляді плунжер-гільз, обгрунтовано ії використання в математичних моделях гідроапаратів з вібраційнною лінеаризаціею.

 Вступ. У світовій і вітчизняній практиці створення гідроапаратури визначилася тенденція використання гідроапаратів з вібраційною лінеаризацією. Запірно-регулюючи елементи таких гідроапаратів здійснюють осцилюючий рух з великою частотою і малою амплітудою, усуваючи, таким чином, силу сухого тертя. Вони застосовуються в високодинамічних та високоточних слідкуючих гідроагрегатах, значно покращуючи характеристики останніх. В процесі проектування таких гідроапаратів виникає необхідність в докладному визначенню окремих складових їх математичних моделей, в тому числі і сили тертя.

Аналіз публікацій. Одним з основних параметрів роботи пари плунжер-гільза, що визначає її якість, є сила тертя спокою, величина якої для реальної пари залежить від величини тиску в гідроагрегаті, збільшуючись зі збільшенням останнього, а також від правильності геометричних форм плунжера і гільзи, співвісності їх розташування [1]. На величину сили тертя впливає радіальний зазор у парі плунжер-гільза, матеріал, з якого вони виготовлені, якість обробки, форма, фізико-хімічні властивості робочої рідини, що використовується в гідроагрегаті, її температура, а також наявність у ній абразивних часток. Вплив на силу тертя матеріалу і якості його обробки досить докладно розглянуті в роботах [2, 3]. Можливості зменшення за їх рахунок сили тертя, на сьогодні, практично вичерпані, тому далі їх розглядати не варто. Недоліком пари плунжер – гільза є облитерація  і гістерезис, усуненням яких може послужити використання вібраційної лінеаризації.

Ціль і завдання дослідження. Уточнення аналітичної залежності для розрахунку сили тертя на запірно-регулюючому елементі гідроапаратів з вібраційною лінеаризацією.

Аналітична залежність для розрахунку сили тертя на запірно-регулюючому елементі гідроапаратів з вібраційною лінеаризацією. При визначені сили тертя вважаємо, що розташування запірно-регулюючого елементу відносно втулки завжди асиметричне, а основним фактором, що визначає таке положення запірно-регулюючого елементу, є пружина. 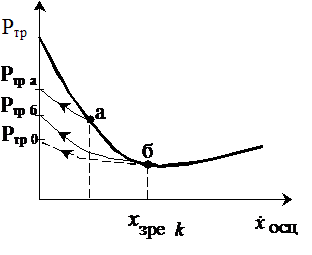При русі запірно-регулюючого елементу сила тертя, з достатньою для практичних розрахунків точністю, може бути описана за допомогою кривої Штрибекка, ідеальний вид половини якої показаний на рис. 1. Залежність  в області 0 << неоднозначна, тому що сила тертя при = 0 (сила тертя спокою), залежить від швидкості, при якій запірно-регулюючий елемент починає рухатися в протилежний бік (рис. 1). Найкращий випадок, коли рух у протилежний бік почнеться в точці б, при цьому, сила тертя в точці =0 прагне до свого мінімального значення. Отже, оптимальна швидкість осциляції запірно-регулюючого елементу повинна дорівнювати . Сила тертя, значною мірою, залежить від ексцентриситету пружини, який залежить від її розміщення в гідроапараті, та може бути визначений з залежності:

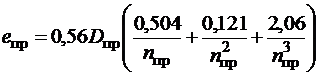                                                                      (1)                      

де –середній діаметр пружини; –число робочих витків пружини.

Значення  розраховано за формулою:

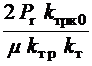                                         =,                                            (2)

де 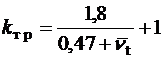,  – коефіцієнт кінематичної в’язкості робочої рідини () – коефіцієнт, що характеризує положення запірно-регулюючого елемента в гільзі; – коефіцієнт динамічної в’язкості робочої рідини; =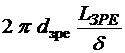– коефіцієнт тертя; -        -радіальний зазор.

 

Розрахунок сили тертя будемо проводити, використовуючи її складові. Вважаємо, що запірно-регулюючий елемент займає асиметричне положення і має точки контакту з гільзою, а кут перекосу зневажливо малий. Використовуючи залежність (1), радіальну силу розраховуємо згідно залежності:

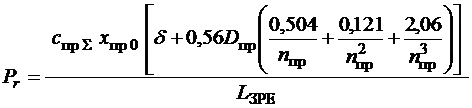                          (3)             

де  – коефіцієнт, який характеризує зміну сумарної жорсткості пружин в гідроапараті з гідравлічним вібраційним контуром або новим гідравлічним вібраційним контуром   в залежності від змінної гідродинамічної сили, жорсткості рідинної пружини, маси запірно-регулюючого елементу, амплітуди та частоти  осциляції;  – попередній підтиск пружини. Кут нахилу вектора швидкості потоку робочої рідини до осі запірно-регулюючого елементу значною мірою залежить від його дроселюючої кромки.

Тоді, залежність для розрахунку сили сухого тертя може бути записана у вигляді:

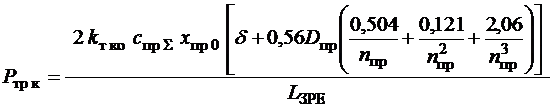         (4)              

Уточнимо також залежність для розрахунку сили рідинного тертя, в яку підставимо коефіцієнт – , який враховує положення запірно-регулюючого елемента в гільзі, і розраховується за уточненою нами залежністю:

                                              ,

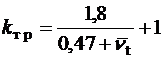де  – відносний коефіцієнт кінематичної в’язкості робочої рідини, . Враховуючи цей коефіцієнт, залежність для розрахунку сили рідинного тертя матиме вигляд:

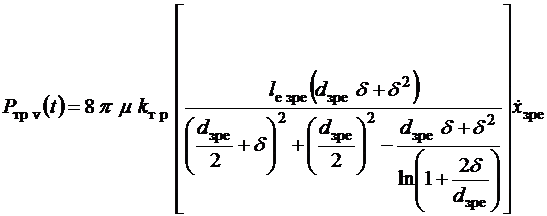           ₍₅₎

 

Підставляючи у формулу

 

,                                          (6)

яка враховує як силу сухого – , так і силу рідинного тертя –, отримали уточнену нами залежність для розрахунку сили тертя запірно-регулюючого елементу гідроапаратів з вібраційною лінеаризацією у  гідравличному  вібраційному  контурі, яку  також можно використовувати для нового гідравличного вібраційного контура:

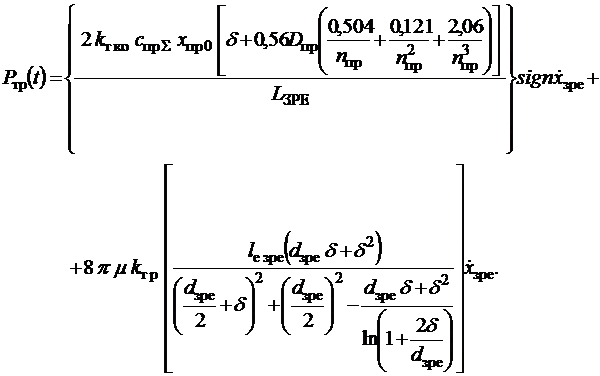          (7)

    

Відзначимо, що знаючи значення критичної швидкості руху запірно-регулюючого елементу (залежність (2)), можемо визначити характер процесу тертя. Якщо при максимальній швидкості руху запірно-регулюючого елементу змащування рідинне, то його зворотно-поступальній рух починається в умовах змішаного змащування, а в середині полуперіоду відбувається перехід до рідинного змащування. Зміна сили тертя відбувається так, як показано на рис. 2 пунктирною лінією.

 

 

Висновки.  Уточнена аналітична залежність для розрахунку сили тертя запірно-регулюючого елемента гідроапаратів з вібраційною лінеаризацією при зворотно-поступальному русі, яка крім параметрів осциляції запірно-регулюючого елементу, враховує його розташування в гільзі, конструктивні параметри пари тертя, наявність у робочої рідини абразивних часток, а також її температуру.

 

Список літератури: 1. Башта Т.М. Гидравлические приводы летательных аппаратов. – М.: Машиностроение, 1967. – 495 с. 2. Андренко П. Н., Асатрян Р. Я.., Клитной В. В. Определение коэффициента расхода и гидродинамической силы предохранительного клапана прямого действия с запорным органом, выполненным в виде золотника / Харьк. гос. политехн. ун-т. – Харьков, 1996, – 16 с. – Деп. В ГНТБ Украины 21.02.96, №598 –Ук 96. 3. Андренко П.Н., Дмитриенко О.В. К вопросу о расчете интерференционного преобразователя пульсаций // Информационные технологии: наука, техника, технология, образование, здоровье. – Харьков: ХГПУ,  1999.– ч. 2 - вып.  7.– С. 10-15.  4. Андренко П. Н. Вибрационная линеаризация – эффективный путь улучшения динамических характеристик гидроаппаратов. Вибрация в технике и технологиях. – Винница: Винницкий государственный аграрный университет, 2003. - №2(28), С. 39 – 45. 5. Зайончковський Г.Й. Оцінка стійкості і протифлатерних властивостей гідромеханічних рульових слідкуючих приводів // Промислова гідравліка і пневматика. – Віниця: ВДАУ, 2006. – №1 (11). – С. 53 – 58.