Content
Introduction. Rationale for news
Goals and objectives. Scientific novelty
Choise of technical limitations and optimization parameters for mathematical models
Introduction. Rationale for news
Despite more than 80 years experience in manufacturing parts from hard materials, engineering plants have great difficulty in mastering the technology of machining workpieces made of these materials. Reduced cutting speed increases the complexity of manufacturing products.
An attempt to intensify the machining by entering the cutting zone of additional energy (cutting with preheating of cut, treatment with the introduction of cutting zone of ultrasonic vibrations, etc.), as well as replacing machining electrical, electrochemical did not find significant applications. The traditional cutting of metals is in the near future will remain the main method of manufacturing precision machine parts, including from hard materials.
Therefore the development of sound technological advice on the choice of rational conditions of the cutting process and the optimal design tool for machining operations of workpieces widely used hard-steels and alloys is very urgent. The most studied turning of hard-metals, the process of drilling these materials still poorly understood.
Goals and objectives. Scientific novelty
The aim is to increase processing performance and durability of the axial hole tool for processing hard materials.
To achieve this goal it is necessary to accomplish the following tasks:
- Consider the classification, physical-chemical and mechanical properties and scope hard materials.
- Explore the nature of the percolation of thermal phenomena in machining of the materials.
- Examine methods of improving processing performance at the expense of informed choice SOTS.
- Consider the optimization of the cutting of stainless and heat resisting steels and alloys.
- Develop a mathematical model to calculate the optimum conditions of drilling.
- Develop a process of manufacturing parts allowing for the processing of this material.
Alleged scientific novelty lies in determining the patterns of influence on the SOTS cutting conditions for drilling. Determination of optimum cutting conditions for given processing conditions, while ensuring high efficiency of penetration of coolants in cutting zone and the effective removal of chips, will increase processing capacity, reduce production costs, and improve the quality of processed holes.
Choise of technical limitations and optimization parameters for mathematical models
Although there are many works devoted to the application of COTS in the machining, the issues associated with using them in the processing of hard materials, not been adequately studied.
Existing work on the optimization does not cover the area of ??processing of special grades of stainless, heat-resistant and high strength steels and alloys. Existing guidelines for choosing rational parameters of processing of these materials contain limited information on the impact of the functional properties of SOTS on cutting conditions. Insufficient information and to assess possible level of productivity when using different coolants, which makes the rationale for their choice in different treatment conditions.
This raises the question of creation of mathematical models for calculating cutting conditions hard materials, taking into account the influence of cutting temperature and SOTS.
It is obvious that the treatment of hard-alloy steels and one of the first technical constraints to optimize and control the processing temperature should be used in the cutting zone.
Limitation 1. Permissible temperature of the cutting.
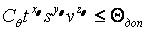
where t — depth of cut, mm;
S — feed, mm / rev;
V — cutting speed, m / min;
Cλ — a constant that takes into account cutting conditions;
xλ, yλ, zλ — exponents.
Limitation 2. Cutting tool possible.
Establishes a relationship between cutting speed, caused adopted tool life, cutting depth, feed, on the one hand, and cutting speed determined by the machine kinematics, on the other side.
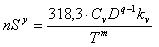
where Cv — a constant factor that characterizes the regulatory conditions of treatment;
D — diametr tool, mm;
Kv — total correction factor for cutting speed;
T — adopted tool life, min;
m — index of relative stability;
q — the exponent of D.
Limitation 3,4,5,6. The kinematics of the machine (the lowest and the highest allowable speed and feed the machine).
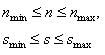
Limitation 7. Electric drive of the main motion machine.
Establishes the relationship between effective power expended in the process of cutting, and electric power of the main motion machine.
Take into account that the torque arising due to cutting forces must be less than the torque of the developed tools for the power of the motor installed on it, that is
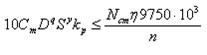
where Сm — a constant factor that takes into account the effect on cutting force of the material and other conditions of treatment;
Кр — total correction factor that takes into account the conditions of treatment;
q, y — exponents, respectively, for D, S;
Nст — main drive electric motor lathe, KW;
n — the efficiency of transmission from the motor main drive to the tool.
Transforming the inequality, we obtain
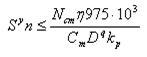
Limitation 8. Given the performance of the machine.
Machine capacity is determined from the expression
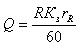
where R — the theoretical performance of the machine, pieces per hour;
Кз — the load factor machine;
rR — number of parts processed simultaneously on a single position.
Cycle length of the machine Тц = 1/Q , or
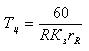
The cycle time is determined by the formule
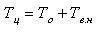
where То — the main technological time, min;
Тв.н — support does not overlap time, min.
The basic process time is determined by the formule
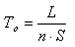
where L — length of the stroke tool.
Given that the cycle time of the machine tool must be greater than the cycle time determined by the sum of (Т0 + Тв.н) the following inequality
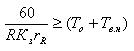
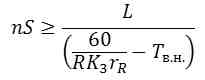
Limitation 9. The strength of the feeder machine.
Feed force Ро, acting on the tool, should not exceed feed force CNC Cutting Pпод.ст..
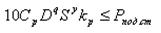
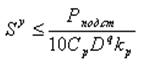
Limitation 10. The strength of the cutting tool.
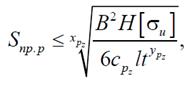
Limitation 11. Rigidity of the cutting tool.
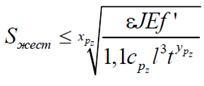
Optimality criterion should be adopted during the main process (or the inverse of the nS):
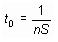
nS — max
Selected technical limitations, reflecting with some precision the physical process of cutting in conjunction with the optimality criterion allows us to construct a mathematical model of the cutting process. However, the task of optimizing cutting conditions with the use of power curves for the technical limitations presents certain difficulties.
One of the first approaches to parametric optimization process is the method of linear programming. The basis of this method is to construct a mathematical model that includes a set of technical limitations and a simplified view of the evaluation function, reduced to linear form by taking logarithms. To solve this problem can be used brute force, Simplex and others, as well as graphic, visually representing mathematical model of the cutting process[6].
To use the method of linear programming is the linearization of the evaluation function and constraints by taking the logarithm and bringing to mind::
a1iln(n) + a2iln(S) = biIe obtain a mathematical model of the cutting process, expressed by a system of linear inequalities that limit the range of permissible values of n and S.
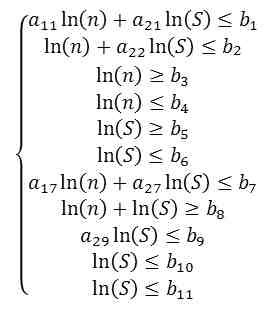
Graphical interpretation of technical limitations, is presented in Figure 3.1. In this case, every technical limitation is the boundary line that defines the half-plane, where the possible existence of solutions of inequalities. Numbers correspond to the numbers of lines selected constraints. Boundary lines intersect to form a polygon of solutions, within which every point satisfies all the inequalities, without exception.
Rare shading denotes the range of values of n and S, allowed the machine kinematics. Frequent shading denotes the range of values of n and S, satisfying all the technical restrictions.
Admissible solutions of linear programming problem is a convex polygon with a finite number of vertices. This means that the extremum of the evaluation function is always global, and achieved one of the vertices of the polygon.
Therefore, the finding of the cutting conditions to ensure maximum performance, will be made direct search of the vertices and choosing the maximum value of the evaluation function (point nS in the figure)[7].
 |
| Fig. 1 — Graphical interpretation of technical limitations. |
The graph illustrates that when drilling hard materials the optimum values ??of cutting conditions are determined by the temperature limits (line 1) and constraints on a given machine performance and durability of the feeder machine, given the lines 8 and 9.
Established that during drilling of the materials the optimum values ??of cutting conditions do not depend on restrictions on the possibilities of cutting tool (line 2), the kinematic constraints of machine (3,4,5,6), cutting power (7), strength and rigidity of the cutting tool (10 , 11).
When using the coolant temperature limit (line 1) is removed, then the optimal values of both feed and cutting speed increase, which leads to increased processing performance.
The use of different coolant temperature limits (1) do not count on the forefront restrictions on cutting tool capabilities (2) and the rigidity of the cutting tool (11), also take into account the constraints given power machine (8), on the strength of the feeder machine ( 9) and its kinematics (5). In this simplified form of a mathematical model of the drilling and it is possible to calculate the cutting conditions and analytical method.
Conclusion
As a result of a mathematical model is supposed to establish the influence of coolant on cutting temperature and optimum performance cutting conditions for drilling products from hard materials, as well as to evaluate the possibility of increasing the productivity of their treatment by using different coolant, using the method of linear programming by the criterion of maximum productivity.
References
1. Обработка резанием жаропрочных сталей, сплавов и тугоплавких металлов. А.М. Даниелян, П.И. Бобрик, Я.Л. Гуревич, И.С. Егоров /Под. ред. Гуревича Я.Л. — М. «Машиностроение», 1965. — 308с.
2. Подураев В.Н. Резание труднообрабатываемых материалов. — М., «Высш. школа», 1974. — 587с.
3. Пестрецов С.И. Компьютерное моделирование и оптимизация процессов резания: учеб. пособие / С.И. Пестрецов — Тамбов: ТГТУ, 2009 — 104 с.
4. Латышев В.Н. Повышение эффективности СОЖ. — М., «Машиностроение», 1975 — 88 с.
5. Режимы резания труднообрабатываемых материалов: Справочник / Я.Л. Гуревич, М.В. Горохов, В.И. Захаров и др. 2-е изд., перераб. и доп. — М.: «Машиностроение» , 1986 — 240с.
6. Оптимизация технологических процессов механической обработки / Рыжов Э.В., Аверченков В.И.; Отв. ред. Гавриш А.П.; АН УССР. Ин-т сверхтвердых материалов. — Киев: «Наук. думка», 1989. — 192 с.
7. Исследование и разработка методики расчета оптимальных параметров режимов резания на токарных станках с ЧПУ. Б. М. Бржозовский, А. Л. Плотников, А. О. Таубе. [Электронный ресурс]. — Режим доступа: http://users.kpi.kharkov.ua/cutting/articles/000005/000005.html
8. Макаров А.Д. Оптимизация процессов резания. — М., «Машиностроение», 1976 — 278 с.
9. Лакирев С. Г. Обработка отверстий: Справочник. — М.: «Машиностроение», 1984. — 208 с.
10. Якобс, Г.Ю. Оптимизация резания. Параметризация способов обработки резанием с использованием технологической оптимизации / Г.Ю. Якобс, Э. Якоб, Д. Кохан. — М.: «Машиностроение», 1981. — 279 с.
Remark! When I wrote this abstract, master's work is not yet completed. The definitive variant will be ready by December, 2011. Full text of work and materials on the subject can be obtained from the author or his adviser after that date.
Top


