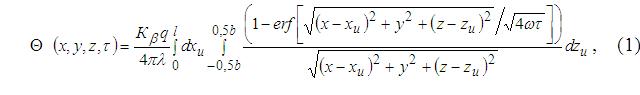
Источник: Молодая наука ХХI века: Сборник научных работ международной студенческой научной конференции. Краматорск: ДГМА, 2011. – С.
В результаті проведених досліджень розроблена методика аналітичного визна-чення температур в деталі та інструменті під час фрезерування з урахуванням урив-частого різання в умовах сталого теплообміну. Встановлений вплив співвідношення між тривалістю робочого і холостого ходів на температуру.
Тепловий стан деталі та інструменту суттєво впливає на працьоздатність різального інструменту та якість обробленої поверхні деталей машин, у зв'язку з чим зростає і актуальність задач по його дослідженню. В наступний час досить добре розроблені методи досліджень теплового стану інструменту і деталі в умовах сталого теплообміну [1]. Відомі дослідження загальнотеоретичних закономірності опису теплофізичних явищ при несталому теплообміні [2], в тому складі для фрезерування [3], не враховують особливостей формування теплових потоків та стану деталі і вимагають подальшого розвитку. Метою представленої роботи є розробка методики розрахунку температур в деталі та інструменті під час фрезерування. Під час схематизації компонентів технологічної системи деталь розглядається як напівскінчений простір, лезо інструменту розглядається у вигляді необмеженого клина з кутом загострення . Джерело теплоти, що виникає на передній поверхні леза інструмента, представляється двовимірним прямокутним з розмірами bхl (l — довжина контактної площадки стружки з передньою поверхнею леза в напрямку сходу стружки, b — ширина контактної площадки). Температурне поле, що виникає в лезі ріжучого інструменту під дією двовимірного прямокутного джерела при несталому теплообміні, описується наступним чином [1]:
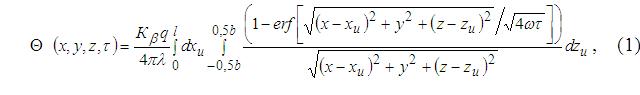
де K — коефіцієнт переходу від необмеженого простору до необмежено-го клина: K = 4 для B=90°, K = 6 для B=60°; q — щільність розподілу теплового потоку; L — коефіцієнт теплопровідності; R — відстань від будь якої точки тіла М(х, у, z) до місця спалаху джерела J(хи, уи, zи):

— відома модифікована функція інтегралу вірогідності. Розрахунки середньої температури леза досить складні, тому для подальшого аналізу теплового стану інструменту як основний його показник приймається температура характерної точки леза — його вершини , яка представлена в безрозмірному вигляді:

де T = x/l, wu= xu/l, w = z/l, Tu= zu/l, l = y/l — безрозмірні координати; s = 0,5b/l — безрозмірна ширина перерізу; Fo= 1 /l2 — безрозмірний критерій часу, або критерій Фур'є.
Такий опис закону розподілу температур у безрозмірному вигляді дозволяє встановити загальні закономірності зміни температури, які для кожного конкретного варіанта обробки коректуються розмірним коефіцієнтом P = Kql/4 , а температурне поле. Процес фрезерування характеризується наявністю робочих ходів тривалістю tp, які чергуються з холостими ходами тривалістю tp. В період робочого ходу відбувається нагрів інструменту, який описується наведеними раніше аналітичними залежностями. В період холостого ходу у відсутності нагріву відбувається охолодження ріжучих кромок за рахунок відведення тепла із зони різання углиб леза. Процес охолодження в цьому випадку описується наступним чином [1]:
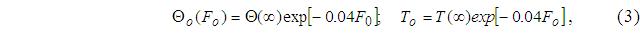
де, Т — абсолютна та безрозмірна температури при сталому теплообміні. Циклічний процес зміни температури вершини леза інструменту при уривчастому різанні, представлений на рис. 2, має аналітичний опис:
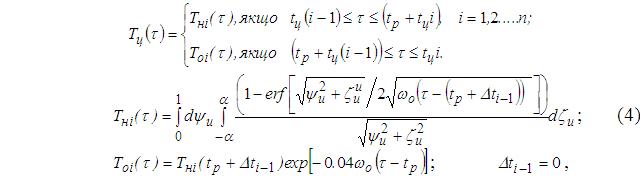
де lо = 1 /l2; tц — тривалість циклу: tц = tp+ tх ; fi — період часу, що корек-тує початок відліку температури нагріву Тн(i+1)(tр+tцi+ti) в кожному наступному циклі з обліком охолодження в передуючому Тоi (tцi): для кожного циклу ti = xi розраховується чисельними методами як корінь рівняння:

Графіки на рис. 1 побудовані для обробки фрезами з твердосплавними пластинами Т15К6 (коефіцієнт температуропровідності l = 0,1001 0 — 4 м2/с) в умовах, що забезпечують розміри контактної площадки стружки з передньою поверхнею леза l = 1мм, b = 2мм, тривалість робочого ходу tp = 0,2с, холостого tх = 0,4с.

У першому циклі tц1 в початковий момент часу спостерігається різке зростання температури протягом першого робочого ходу tp до точки 2 (Тн1 (tp) = 2,75) на кривій нагріву ТН, а потім протягом холостого ходу tx відбувається охолодження до точки 4 (То1 (tц) = 2,34) на кривій охолодження ТО. Розраховане значення l1 = 0,08. У наступному циклі tц2 нагрів в період робочого ходу tp походить від точки 4 до точки 6 (Тн2(tp+ tц) = 2,86) по кривій, відповідній ділянці 1-3 кривої нагріву ТН, потім знов відбувається охолодження до точки 8 (То2(2tц) = 2,44). Розраховане значення l2 = 0,617. Наступний цикл tц3 починається в точці 8, нагрів протягом робочого ходу tp відбувається по кривій 8-9 (Тн3(tp+ 2tц) = 2,88), відповідній ділянці 5-7, охолодження закінчується в крапці 10 (То3(3tц) = 2,45), потім процес знов повторюється. Розраховане значення l31 = 1,203 свідчить про те, що з погрішністю 0,3% процес стабілізується — нагрів і охолодження врівноважуються, і може вважатися сталим.

Середній рівень температури, досягнутої при сталому уривчастому різанні ТЦср нижче, ніж при безперервному Т, що може бути порівняно за допомогою наступного коефіцієнта. Графіки залежності коефіцієнтів зниження рівня температур при уривчастому різанні в порівнянні з безперервним КТ від співвідношень робочих і холостих ходів наведені на рис. 2 (тривалість циклу постійна tц = cоnst, зміна тривалості робочого ходу характеризується коефіцієнтом Кц = tр/tц). Прийнято, що Т(100)= 3,5. Джерело теплоти на поверхні деталі представляється смуговим швидкорухомим з розміром L, який визначається довжиною контакта деталі з лезом інструменту в межах зносу по його задній поверхні h (L = h). Температурне поле в деталі для швидкорухомого смугового джерела описується аналітичним виразом [1]:

де L — розмірний коефіцієнт; Pe = Vl/tд — критерій Пеклє. Розподіл безрозмірних температур у поверхневому шарі деталі:

де дріб — рівномірна та нормальна несиметрична функції розподілу щільності теплових потоків.
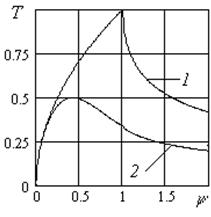
Розподіл безрозмірних температур на поверхні деталі для рівномірного (крива 1) та нормального (крива 2) законів розподілу щільності теплових потоків Т:

Максимальне значення безрозмірних Т1max і Т2max та розмірної температур Smax з урахуванням їх координат згідно з рис. 3: T2max(0.5,0) = 0.5; T1max(1,0) = 1; T2max = Ро Тmax. Розроблена методика дозволяє розраховувати температуру в будь який точці деталі.
Таким чином, в результаті проведених досліджень розроблена методика аналітичного визначення температур в деталі та інструменті під час фрезерування з урахуванням уривчастого різання в умовах сталого теплообміну. Встановлений вплив співвідношення між тривалістю робочого і холостого ходів на температуру, що дає оцінку зниження температури інструменту під час уривчастого різання порівняно з безперервним для різних умов обробки.