Известно, что если под действием статической нагрузки определенного вида возможна потеря статической устойчивости, то под действием вибрационной нагрузки того же вида возможна потеря динамической устойчивости. Подобная нагрузка называется параметрический и вызывает параметрический резонанс.

Характерным примером систем, испытывающих параметрический резонанс, являются осевые инструменты: сверла, зенкеры и развертки при резании металлов и буровые штанги при бурении скважин. Для таких инструментов характерна значительная длина и относительно небольшая изгибная жесткость. Как правило, такие инструменты испытывают значительную продольную силу P0, которая может вызвать потерю устойчивости. Вместе с тем, большинство осевых инструментов в процессе работу имеют динамическую составляющую продольной силы, которая может стать причиной возникновения параметрического изгибного резонанса.

Для осевого инструмента характерны две схемы закрепления: с условным шарнирным закреплением концов и с жестким и шарнирным закреплением. Рассмотрим характер возникновения изгибного параметрического резонанса на примере осевого инструмента с шарнирным закреплением концов (рис.1).

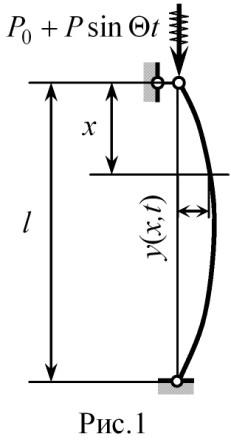
Предположим, что в процессе работы инструмента вследствие каких-то причин осевая сила Р0 получила динамическое приращение P(t)=PcosOt. Тогда дифференциальное уравнение поперечных колебаний осевого инструмента, как весомого стержня с погонной массой m с учетом сил инерции примет вид

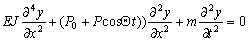(1)

Обозначив

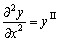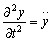,, (2)

получаем

(3)

Решение этого уравнения известно в виде:

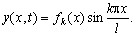(4)

После подстановки решения (4), уравнение (3) можно представить в виде

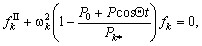(5)

где 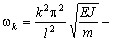k-я собственная частота, - k-я критическая сила.

Вводя обозначения

(6)

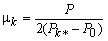(7)

уравнение (5) при k=1 приводится к виду

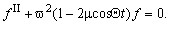(8)

Уравнение такого вида известно как уравнение Матье. В более общей форме оно известно как уравнение Хилла

(9)

Одним из основных свойств этих уравнений является наличие областей динамической неустойчивости, которые возникают при некоторых соотношениях между коэффициентами wk и и когда оно имеет неограниченно возрастающие решения. В работе [2] установлено, что наиболее опасной является первая (главная) область неустойчивости, границы которой для уравнения (4) определяются выражением

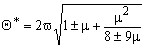(10)

Верхняя и нижняя границы второй области определяются зависимостями

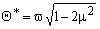и (11)

Границы третьей области определяются выражением

(12)

На Рис.2 приведена диаграмма для первых трех зон неустойчивости, выраженные в относительных единицах. Зоны неустойчивости для более низких частот обычно вырождаются в «скелетные» линии.

Рис.2

Для решения конкретных практических задач по определению неблагоприятных соотношений между коэффициентами уравнения (5) необходимо знать характер изменения динамической составляющей P(t). Анализ исследований различных авторов [3-6] показывает, что основными причинами возникновения динамической составляющей продольной силы при работе осевого инструмента являются периодические составляющие сил резания, вызванные неточностью изготовления и заточки режущего инструмента, резание по «следу», оставленному предыдущей режущей кромкой, динамические процессы в технологической системы и другие причины.

В рассматриваемом случае гармонической форме динамической составляющей осевой силы РcosОt хорошо соответствуют периодические силы резания, возникающие за счет неравномерной заточки инструмента. Амплитудное значение динамической составляющей осевой силы для основных видов осевого инструмента согласно нормативам равно (0,2-0,5)Р0, то есть

(13)

Частота динамической составляющей О выражается через скорость резания v и диаметр обрабатываемого отверстия d соотношением

(14)

Постоянная составляющая осевой силы при работе осевого инструмента определяется соотношением

(15)

и является функцией подачи s и глубины резания t. После подстановки (13) и (15) коэффициен-ты (6) и (7) приводятся к виду

(16)

(17)

а диаграмма областей динамической неустойчивости (10)-(12) легко преобразуется к практической системе координат с осями v (скорость резания) и s (продольная подача на один оборот осевого инструмента).

Другой объективной причиной возникновения гармонической динамической составляющей осевой силы для осевого инструмента является резание по «следу», оставленному предыдущим инструментом или предыдущей режущей кромкой одного инструмента. При этом на i-ю режущую кромку инструмента будет воздействовать периодическая сила.

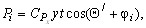(18)

где n — число режущих кромок предыдущего инструмента, О — частота вращения инструмента, y — погрешность обработки на предыдущей операции.

Суммарная периодическая осевая сила определится зависимостью

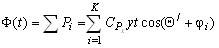(19)

где К — число режущих кромок на данном проходе.

Для дальнейших расчетов зависимость (19) удобно представить в гармонической форме рядов Фурье

после подстановки которых в уравнение Хилла (6), оно принимает вид

В работе [2] показано, что в первом приближении границы k-й области неустойчивости для уравнения (20) зависят лишь от соответствующей гармоники ряда Фурье и могут быть с достаточной точностью определены по формуле

Подобный подход справедлив в большинстве случаев и для более сложных вариантов нагружения. Учитывая сложный характер процесса резания и взаимодействия инструмента с обрабатываемой деталью и окружающей средой для более точной оценки режимов резания необходимо использовать более сложные выражения для пульсирующей составляющей осевой силы. Однако все они легко представляются в гармонической форме рядов Фурье и могут быть использованы при решении уравнения Хилла.

Практическое значение построения диаграмм динамической неустойчивости для осевого инструмента заключается в следующем:

1) они позволяют определить неблагоприятных соотношений между параметрами режимов резания. Так, в рассмотренном на рис.3 случае в первую область динамической неустойчивости попали некоторые сочетания скоростей резания и подачи, которые рекомендованы ГОСТом для данного инструмента.

2) они позволяют выделить виды и типоразмеры осевых инструментов, для которых возможна потеря динамической устойчивости. Для большинства коротких осевых инструментов все области динамической неустойчивости вырождаются в «скелетные» линии имеющие малую ширину и не позволяющие возникать устойчивому резонансу.

Литература

1. Пономарев С.Д. и др. Расчеты на прочность в машиностроении. Ч. 3. М.: Гостехиздат, 1959. — 1120с.

2. Болотин В.В. Динамическая устойчивость упругих систем. М.: Гостехиздат, 1956. — 600с.

3. Кудинов В.А. Динамика станков. М.: Машиностроение, 1967. — 400с.

4. Подураев В.Н. Обработка резанием с вибрациями. М.: Машиностроение, 1970. — 352с.

5. Орликов М.Л. Динамика станков. К.: Вища школа, 1980. — 256с.

6. Василенко Н.В. Теория колебаний. К.: Вища школа, 1992. — 432с.

7. Филиппов Г.В. Режущий инструмент. М: Машиностроение, 1981. — 392с.