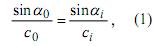
Источник: http://www.ktu.lt/ultra/journal/pdf_58_1/58-2006-Vol.1_04-L.Jakevicius.pdf
Проанализированы
возможности измерения толщины слоя и скорости распространения
ультразвуковых сигналов в слоистых структурах с использованием угловых
электроакустических преобразователей с известными параметрами.
Показано, что, когда скорость распространения ультразвуковых сигналов в
отдельном слое структуры неизвестна, толщина и скорость распространения
сигналов в них может быть измерена с помощью одного измерительного
канала с угловыми ультразвуковыми преобразователями. Разработаны
алгоритмы для определения толщины отдельных слоев и скорости
ультразвука в них в случае, когда слоистая структура облучается под
известным углом к поверхности структуры. Выполняется моделирование
измерительного канала с угловыми ультразвуковыми преобразователями. При
моделировании выявлены распространение и отражение ультразвуковых
сигналов в дюралюминий - оргстеклянной слоистой структуре и
пространственные и временные распределения их на поверхности слоистой
структуры. Изменения временного и пространственного распределения
принятых сигналов исследованы, когда изменяется угол падения излучения
на слоистую структуру. Показано, что временное и пространственное
распределение сдвиговых и продольных волн не совпадают друг с другом и
ведут себя по-разному, когда изменяется угол падения. Представлены
результаты экспериментальных исследований.
Ключевые слова: скорость ультразвука, угловой ультразвуковой датчик,
слоистая структура, поперечная волна, продольная волна.
Ультразвуковые
методы измерения толщины и других физических параметров слоистой
структуры широко используются в промышленности и неразрушающем контроле
[1-4]. Но в настоящее время многослойные структуры становятся все более
сложными, состоящими из материалов с различными механическими и
акустическими свойствами, такими как пластмассы и металлы или металлы,
жидкости и пластмассы. Разница механических импедансов этих материалов
вызывает много проблем. Особенно это очевидно, когда измерительная
информация может быть получена только с одной стороны слоистой
структуры [5,6]. В этом случае не всегда можно получить измерительную
информацию о параметрах всех слоев или некоторые из них. Это
обусловлено потерями ультразвукового сигнала в отдельных слоях, а также
потерями на границах между ними. Эти потери зависят от различия
акустических импедансов и акустических свойств материалов в различных
слоях. Другие трудности возникают из-за того, что акустические свойства
материалов различных слоев часто не известны с достаточной точностью.
По этой причине измерение толщины и других параметров отдельных слоев
является проблематичным. Проблемы связаны с тем, что скорости
распространения акустических волн различных типов в отдельных слоях
структуры неизвестны. В таком случае определение толщины отдельного
слоя возможно только с помощью двух отдельных измерительных каналов. По
крайней мере, в одном канале слой должен быть облучён под углом к его
поверхности. Хотя, при зондировании под углом к поверхности слоя
структуры, продольная, поперечная и другие типы ультразвуковых волн
возбуждаются [1]. Это позволяет увеличить возможности измерения с
помощью ультразвукового режима преобразования волн. Скорость
распространения поперечных волн примерно в два раза меньше скорости
продольных волн. В этом случае время распространения акустических
сигналов в слое становится почти в два раза дольше. Это позволяет
улучшить разрешение и точность измерения толщины. Однако часто в
многослойных структурах скорости распространения различных типов волн в
отдельных слоях неизвестны, особенно для ультразвуковых поперечных
волн. В этом случае углы распространения и отражения ультразвуковых
волн различных типов не известны тоже.
Наклонный метод падения для возбуждения продольных и поперечных волн
очень удобен для измерения неизвестной скорости ультразвука и толщины с
использованием двух каналов измерения [6,7]. В обоих случаях два
измерения проводятся для различных расстояний и времени задержки. Но в
анализе, представленном в [6,7], нет никакой информации об
ультразвуковом режиме преобразования волны и о распространении
поперечных волн в отдельных слоях слоистой структуры. В этих статьях
нет информации об использовании и выборе различных типов волн, а также
информации об использовании угловых преобразователей для этой цели.
Поэтому целью данной работы является анализ и проверка нового метода
для измерения толщины и скорости ультразвука в многослойных структурах
с использованием информации о параметрах угловых преобразователей.
Предположим, что у нас есть среды, которая состоит из n параллельных слоев с различными физическими свойствами. Плоская акустическая волна излучается в эту структуру под углом α0 с использованием углового ультразвукового датчика. Скорость распространения продольных волн в клине датчика составляет c0. Эта волна на каждой границе слоев преобразовывается в отражённые и преломлённые продольные и поперечные волны (рис. 1). С целью не перегружать Рис.1 информацией, изображена лишь одна из преломленных волн. Угол αi распространения любой волны в i слое определяется законом Снеллиуса
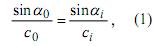
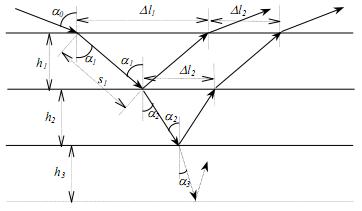
Рис.1.
Распространение и отражение ультразвуковых волн
в многослойной структуре
где ci - скорость распространения ультразвуковых волн в i среде. Будем считать, что скорость распространения ультразвуковых волн c0 и угол α0 излучения волн на клине преобразователя известны. Тогда параметр k, характеризующий клин преобразователя, может быть представлен
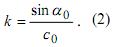
Используя
Рис.1, уравнение sinαi
= ∆l
/2s
и Уравнения 1 и 2
можно получить выражение для пути сигнала si
в i слое
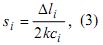
где
∆li
является смещением
акустического сигнала в i
слое в течение
одного излучения-приёма (Рис.1). С другой стороны, путь si
акустического сигнала в i
слое может определяться как
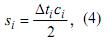
где
∆ti
- время
распространения ультразвукового сигнала в течение
одного шага излучения-приёма. Из Уравнений 3 и 4 можно получить
скорость распространения акустического сигнала ci
в i
слое
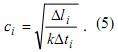
Из
Рис.1 видно, что толщина hi
в i
слое
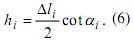
Используя
Уравнения 1, 2 и
Уравнение 5 мы получаем
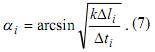
Тогда
толщина hi
в
i слое может быть описана
уравнением
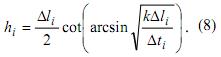
На
практике обычно измеряется
время распространения ti
акустического
сигнала от его передачи до приёма. Это время состоит из времени
распространения ультразвукового сигнала t0
в клинья
электроакустических
преобразователей и время распространения акустического сигнала в
слоистой структуре, в течение которого распространяется сигнал, т. е.
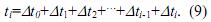
Расстояние
li
удобно измерять между
центрами акустических осей
преобразователей
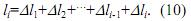
Используя
Выражения 9
и 10, Уравнения 5 и 8 приводятся к виду
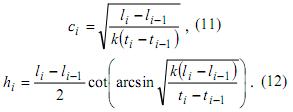
Полученные
результаты показывают,
что зная параметры k
и t0
клиньев
преобразователя и используя разработанные алгоритмы, можно определить
толщину отдельных слоев, а также скорость распространения акустических
сигналов в этих слоях.
С
целью выявления возможности получать алгоритмы на практике, было
выполнено моделирование пространственных и временных распределений
ультразвуковых сигналов, распространяющихся в слоистой структуре. Для
вывода математических уравнений был использован Рис. 1. Как видно из
Рис.1, акустический сигнал, при распространении через n-й
слой,
задерживается на время, значение которого
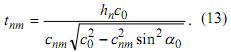
Здесь
n=1,
2, 3,…является номером
слоя; m
обозначает тип
волны (l
- продольные, s
- поперечные). В течение этого
времени
ультразвуковой сигнал распространяется в слое и проходит вдоль
поверхности слоя расстояние
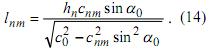
Используя алгоритмы (Уравнения 13 и 14) было выполнено моделирование распространения сигнала в двух слоях дюралюминиво-оргстеклянной структуры. Толщина каждого отдельного слоя составляет 5мм. Возбуждение и прием ультразвуковых сигналов был выполнен с дюралюминиевой стороны слоистой структуры. С целью свести к минимуму количество ультразвуковых волн, возникающих из-за режима преобразования волн, угол падения α0 ультразвуковых продольных волн возбуждаемых угловым датчиком был выбран между первым и вторым критическими углами в дюралюминии. В нашем случае этот угол изменялся между 30о и 50о. По этой причине только поперечные волны могут быть возбуждены в первом (дюралюминиевом) слое. В качестве материала клина углового датчика, с которого ультразвуковые волны излучаются, было использовано оргстекло. Скорость продольных волн в нём cl = 2650 м/с [8]. Первый слой был дюралюминиевым со скоростью поперечных волн cds = 3100 м/с. Второй является границей дюралюминиевого слоя взаимодействующего с оргстеклом, со скоростью продольных волн cpl = 2650 м/с и скоростью поперечных волн cps = 1335 м/с [8].

Рис.2.
Изменение времени
распространения ультразвуковых сигналов в двухслойной
структуре из дюралюминия-оргстекла,
когда меняется
угол
падения
Результаты моделирования, которые показывают пространственное и временное распределение ультразвуковых сигналов, распространяющихся в двухслойную структуру, когда угол падения α0 изменяется от 30о и 50о, показаны на Рис.2 и Рис.3. С целью упростить назначение ультразвуковых сигналов, распространяющихся в слоистой структуре, поперечная волна в дюралюминии была названа индексом t. Поперечные и продольные волны в оргстеклянном слое были помечены индексами s и l соответственно. Номер перед индексом показывает количество переходов соответствующей волны через слой. Первые два символа в индексе обозначают первый слой (дюралюминий) и два последующих - второй слой из оргстекла.
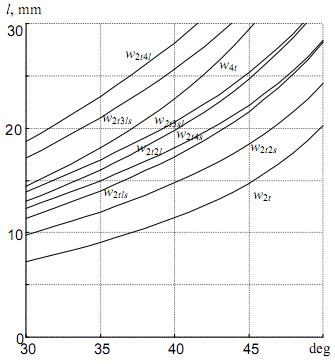
Рис.3.
Изменение расстояния между
точками передачи и приема ультразвуковых
волн на поверхности слоистой структуры при изменении угла падения
Как упоминалось ранее, в дюралюминиевом слое возбуждается только поперечная волна. Часть её энергии отражается от границы раздела дюралюминия-оргстекла и поперечная волна w2t возвращается в принимающий преобразователь (первый шаг излучения - приёма на Рис.4). Поперечные волны на Рис.4 показаны сплошными линиями и продольные волны - пунктирными линиями. Другая часть энергии этой волны на границе дюралюминия-оргстекла трансформируется в поперечные и продольные волны, передающиеся в оргстекло. Во время отражения от границы воздух-оргстекло часть энергии поперечной волны преобразуется в продольную волну. По аналогии часть энергии продольных волн переходит в поперечную волну. После преломления на границе оргстекла-дюралюминия эти волны получены на различных расстояниях от точки передачи (волны w2t2s, w2tls и w2tsl на Рис.4). Часть энергии продольной волны, отраженной от границы оргстекло-воздух, на границе оргстекло-дюралюминий преобразуется в поперечную волну, и в результате получаем волну w2t2s. Но поперечные волны в слое оргстекла, между дюралюминием и газообразной средой, могут быть отражены два или более раз и воспринимается как волны w2t4s. Аналогично, поперечные волны в дюралюминии, между границами с оргстеклом и угловым датчиком, могут быть отражены три или более раз и охватывают достаточно большие расстояния (волны w4t после второго излучения-приёма на Рис.4). В масштабе времени (Рис. 5), как и в масштабе расстояния (Рис. 4), первой полученной волной является поперечная волна w2t, отраженная от границы дюралюминия-оргстекла. Но смещение в масштабе времени других отраженных волн отличается от их перемещения в масштабе расстояния. По этой причине на практике трудно определить тип волны, получаемой на заданном расстоянии или в данный момент. Таким образом, моделирование распространения сигнала в многослойной структуре необходимо перед проведением измерений в реальных условиях.
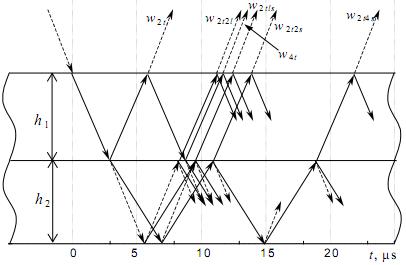
Рис.4. Пространственное распределение ультразвуковых волн в двухслойной структуре дюралюминия-оргстекла
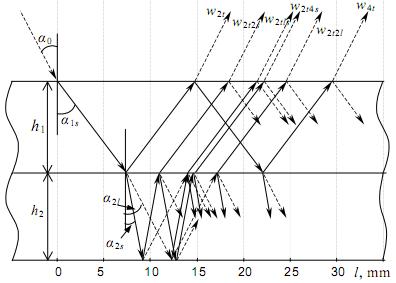
Рис.5. Временное распределение ультразвуковых волн в двухслойной структуре дюралюминия-оргстекла
Экспериментальное
исследование, согласно методу измерения, проводили с использованием
угловых преобразователей с углом падения сигнала на слой структуры
α0
= 44,70.
Клинья ультразвуковых преобразователей были
изготовлены из оргстекла. Скорость продольных волн в клиньях
преобразователей составляла cpl
= 2650 м/с [8]. Для калибровки канала измерения клинья датчиков были
прижаты лицом к лицу
друг с другом и была получена максимальная амплитуда сигнала.
В ходе этого эксперимента были определены время задержки
ультразвукового сигнала в клиньях преобразователей t0
= 6,90 мкс и
расстояние l0
= 10
мм между осями акустических преобразователей.
Частота широкополосных ультразвуковых преобразователей составляла 5,0
МГц. Толщина первого дюралюминиевого слоя, к которому прижимались
преобразователи, составляла 5,14 мм. Второй слой оргстекла приклеен к
первому слою с помощью эпоксидной смолы. Толщина слоя оргстекла
составляла 4,90 мм и толщина клея - 20х10-6
мм.
Результаты расчетов и экспериментальных исследований представлены в
таблице 1. Были получены шесть импульсов поперечных и продольных волн,
когда расстояние между преобразователями изменялось. Используя
результаты измерения, были рассчитаны время задержки и скорость
ультразвука в слоях. Каждое измерение времени задержки и расстояния
между ультразвуковыми преобразователями было выполнено в указанной
позиции в соответствии с амплитудой импульса. Параметр k
клиньев
преобразователя, для угла α0
= 44,7о
и скорости ультразвука в
них cp
= 2650 м/с,
составил 0,2654х10-3.
Таблица 1. Время задержки и расстояние между осями акустических преобразователей
| Отраженная волна | Теоретические | Экспериментальные | ||
| t, мкс | l, мм | t, мкс | l, мм | |
| w2t | 5.84 | 14.9 | 5.97 | 15.0 |
| w2tsl | 13.85 | 18.5 | 13.80 | 18.6 |
| w2t4s | 12.46 | 21.3 | 12.62 | 21.8 |
| w2t2l | 21.86 | 22.2 | 22.71 | 22.7 |
| w2t2s | 11.06 | 24.6 | 11.12 | 24.8 |
| w4t | 11.67 | 29.8 | 11.80 | 30.4 |
Для расчета толщины слоя и скорости ультразвука в нем были использованы Уравнения 11 и 12. Результаты расчета толщины слоя и скорости распространения поперечных и продольных волн представлены в таблице 2.
Таблица 2. Cкорости ультразвука и толщины слоев
| Поперечная волна | Продольная волна | |||
| c, м/с | h, мм | c, м/с | h, мм | |
| Первый слой | 3137 | 5.18 | - | - |
| Второй слой | 1303 | 4.95 | 2634 | 4.95 |
Применяя
угловые преобразователи с известными параметрами клиньев, представлен
новый метод измерения толщины слоев и скорости распространения
ультразвуковых сигналов в этих слоях. Метод основан на измерении
расстояния между осями акустических преобразователей (на поверхности
слоя) и времени задержки сигналов.
Выполняется моделирование распространения ультразвуковых сигналов в
двухслойной структуре дюралюминия-оргстекла. Проанализированы
особенности временного и пространственного распределения ультразвуковых
сигналов и зависимости этих распределений от угла возбуждения волн.
Результаты моделирования показывают, что последовательность принимаемых
сигналов ультразвука на оси расстояния не совпадает с
последовательностью соответствующих сигналов на оси времени. По этой
причине возникают трудности при измерении толщины слоя и скорости
ультразвука в многослойных структурах.
С целью увеличения возможностей измерения и облегчения выбора
измерительных сигналов целесообразно свести к минимуму преобразования
ультразвуковых волн в первом слое. Они зависят от акустических свойств
слоя, а также от угла клина электроакустических преобразователей,
который должен быть выбран между первым и вторым критическими углами
слоя.
1.
Guyott C. C. H., Cawley
P. The measurement of through thickness
plate
vibration using a pulsed
ultrasonic
transducer. J. Acoust. Soc. Am. 1988. Vol. 83. No 2. P.
623-631.
2.
Hsu D.
K., Hughes M. S.
Simultaneous
ultrasonic velocity and sample
thickness
measurement and application in
composites. J. Acoust. Soc. Am. 1992. Vol. 92. No. 2. P.
669-675.
3.
Greco de
Sousa A. , Machado J.
C. ,
Pereira C.A. Ultrasonic characterization of
stratified
media with independent measurement of wave velocity
and thickness. IEEE Ultrasonic
Symposium.
2002. P.853-856.
4.
Cotter D. J., Michaels J.
E., Zhang Z., Ghabour E., Nelligan T., Abbate A.,
Kass D. and Elfbaum
G. High
frequency ultrasonic thickness and
acoustic
velocity measurement methods for advanced material
and component characterization.
NDT net,
October 2002. Vol.7. No.10.
5.
Carodiskey T. J., Meyer
P. A. Thickness measurement in materials of unknown acoustic velocity.
NDT net, October 1997. Vol. 2. No.10.
http://www..ndt.net/article/wt1097/Caro 2/caro 2.htm.
6.
Vilkickas M., Kažys R.
Thickness measurement at individual layers in
sandwich structures with
unknown
ultrasound velocity. Ultragarsas. 2003. Nr.4(49). P.7-15.
7.
Siegel M.
Measurement issues in
quantitative
ultrasonic imaging. IEEE transactions
on
instrumentation and measurement. 1998.
Vol.47. No. 6.
P. 1435-1438.
8.
Hung B.
N., Goldstein A. Acoustic
parameters
of commercial plastics. IEEE
Trans.
Sonics Ultrason. 1983. Vol.
SU-30. No.4.
P.249-254.