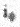 - ток холостого хода двигателя; i, u, m - соответственно ток, напряжение и момент нагрузки АД. Все величины выражены в относительных единицах
- ток холостого хода двигателя; i, u, m - соответственно ток, напряжение и момент нагрузки АД. Все величины выражены в относительных единицахИсточник: XIV международная научно-техническая конференция. Проблемы автоматизированного электропривода. Теория и практика; http://paep2007.abacus.ua/default.aspx?id=paep_show_doc&doc=10982
Введение. Энергетическая оптимизация АД путем плавного регулирования напряжения применяется по отношению к асинхронным электроприводам, использующим тиристорные преобразователи переменного напряжения [1, 4]. В общем случае в качестве критерия оптимизации могут быть минимальные потери, минимальный ток или минимальная активная потребляемая мощность. Регулируемым параметром является напряжение, а в качестве сигнала обратной связи используется скольжение или угловая скорость оптимизируемого двигателя.
Постановка задач исследования. Целью работы является получение законов регулирования для различных способов энергетической оптимизации незагруженного асинхронного электропривода путем плавного регулирования питающего напряжения.
Материалы исследования. Энергетическая оптимизация АД при экстремальном регулировании напряжения по току.
В качестве исходного примем известное выражение для тока АД при неноминальном напряжении [2]:

где 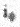 - ток холостого хода двигателя; i, u, m - соответственно ток, напряжение и момент нагрузки АД. Все величины выражены в относительных единицах
- ток холостого хода двигателя; i, u, m - соответственно ток, напряжение и момент нагрузки АД. Все величины выражены в относительных единицах
Взяв производную тока по напряжению и приравняв ее к нулю, получим выражение для оптимального напряжения, при котором ток приобретает минимальное значение:

Подставив оптимальное значение  в исходное выражение для тока, получим зависимость минимального значения тока от момента нагрузки:
в исходное выражение для тока, получим зависимость минимального значения тока от момента нагрузки:
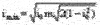
Решая последние два уравнения относительно моментов, получаем: 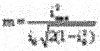 ,
, 
а приравняв правые части обоих выражений 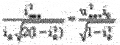 ,
, 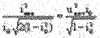
можно получить закон экстремального регулирования напряжения:
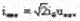
Как видно, закон регулирования выражается линейной зависимостью. Линия 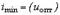 проходит через начало координат, ее крутизна зависит от тока холостого хода двигателя, увеличиваясь с ростом последнего.
проходит через начало координат, ее крутизна зависит от тока холостого хода двигателя, увеличиваясь с ростом последнего.
Энергетическая оптимизация АД путем поддержания оптимального скольжения (скорости)
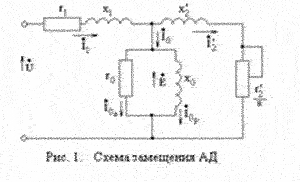
Для обоснования этого способа выразим потери в электродвигателе через параметры его Т-образной схемы замещения [3]
 , (1)
, (1)
где Io - активная составляющая тока намагничивания.
Для упрощения дальнейших выкладок в выражении для потерь не учтены механические и добавочные потери.
Электромагнитная мощность, передаваемая от статора к ротору, равна произведению момента на угловую скорость электромагнитного поля: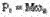
Эта мощность делится на две части, одна из которых передается на вал двигателя, вращающийся со скоростью 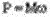 , а вторая часть выделяется в виде теплоты в роторной цепи двигателя:
, а вторая часть выделяется в виде теплоты в роторной цепи двигателя:
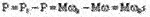 . (2)
. (2)
Если учесть, что для реальных асинхронных машин 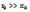 , а при малых значениях скольжений, соответствующих работе двигателя на линейной части его механической характеристики, можно принять, что
, а при малых значениях скольжений, соответствующих работе двигателя на линейной части его механической характеристики, можно принять, что 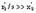 , то можно получить следующие соотношения для схемы замещения:
, то можно получить следующие соотношения для схемы замещения:
 ;
;
 (3)
(3)
где Iop - реактивная составляющая тока намагничивания.
С учетом (3) получаем следующее выражение для потерь:
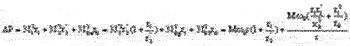 (4)
(4)
где 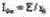 .
.
Как видим, обеспечение минимальных потерь в двигателе требует поддержания постоянного оптимального скольжения, определенного выражением (5). Это свойство АД позволяет обеспечить минимизацию потерь в системе автоматического регулирования с обратной связью по скольжению или скорости
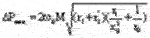
Аналогичные исследования на экстремум выражений для тока статора
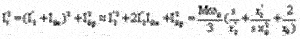
и активной потребляемой мощности

позволяют получить соотношения для скольжений, обеспечивающих: минимум тока статора  ; минимум потребляемой мощности
; минимум потребляемой мощности 
Выводы. Реализация рассмотренного способа энергосбережения АЭП предложена в качестве лабораторного стенда научно-исследовательской лаборатории «Энергосбережение в электроприводе», введенной в эксплуатацию в ИАЭ НУК. Предусмотрены два режима работы установки: ручной, при схемах соединения статорной обмотки «звездой» и «треугольником»; автоматический. В ручном режиме осуществляется экспериментальное определение энергетических характеристик двигателя. В автоматическом режиме путем поддержания постоянной оптимальной скорости и соответствующего изменения напряжения обеспечиваются условия минимальных потерь при изменениях нагрузки от m=0 до m=1 .