Источник: XIV международная научно-техническая конференция. Проблемы автоматизированного электропривода. Теория и практика; http://paep2007.abacus.ua/default.aspx?id=paep_show_doc&doc=11050
Введение. Современные системы векторного управления позволяют просто и эффективно управлять такими сложными объектами, как асинхронный двигатель с короткозамкнутым ротором [1]. Для реализации векторного управления необходимо знать информацию о состоянии электродвигателя, что раньше достигалось установкой датчиков внутри двигателя. Математическое моделирование электромагнитных процессов электродвигателя [2] позволяет отказаться от использования физических датчиков. В системах векторного управления напряжение на зажимы двигателя подается от преобразователя частоты и содержит высшие гармоники, которые могут нести полезную информацию о состоянии двигателя. Использовать классическую модель Горева-Парка можно только при идеальном синусоидальном напряжении статора, которое во вращающейся системе dq-координат становится константой. Выделяя из несинусоидального напряжения гармонические составляющие, можно применять уравнения Горева-Парка отдельно для каждой составляющей. В [3] рассмотрены принципы вычисления результирующего момента.
Постановка задач исследования. Искусственное введение высших гармоник в напряжение питания, в частности, седьмой гармоники, позволит проводить диагностику двигателя в рабочем режиме, подвергая токи и напряжения статора спектральному анализу. Требуется показать влияние высшей (седьмой) гармоники на работу АД.
Материалы исследования. Для записи уравнения момента рассмотрены схемы двух машин: с двумя статорами и двумя роторами, соединенными муфтами (рис. 1), и с двумя статорами и общим ротором (рис. 2).
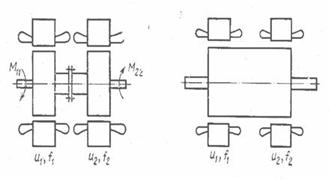
В первом случае (рисунок 1) все гармоники создают моменты, вращающие роторы первой и второй машин
М = М11 + М22. (1)
В схеме с общим ротором (рисунок 2) существует связь между гармониками, и уравнение момента приобретает вид
М = М11 + М12 + М21 + М22. (2)
Для исследования установившегося режима работы асинхронного двигателя можно использовать модель по рис. 1, для динамического режима – модель по рис. 2.
В результате проделанной работы была создана расширенная система уравнений Горева-Парка (3), в основу которой положена модель, представленная на рис. 1:
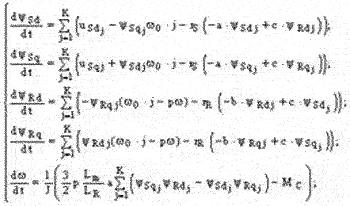 (3)
(3)
где a = LR /( Lm2 - LS LR); b = LS /( Lm2 - LS LR); c = Lm /( Lm2 - LS LR); ? – угловая скорость вращения ротора; J – момент инерции электропривода, приведенный к валу двигателя; LS – индуктивность фазы статора; LR – индуктивность фазы ротора; Lm – взаимная индуктивность обмоток статора и ротора; MC – статический момент нагрузки; р – число пар полюсов двигателя; rS(rR) – активное сопротивление фазы статора (ротора); uSd, uSq – проекции напряжения статора на оси d, q для соответствующей гармоники j; ?Sd, ?Sq, ?Rd, ?Rq – проекции потокосцеплений статора и ротора на оси d, q для соответствующей гармоники j; ?0 – синхронная скорость; K – общее число рассматриваемых гармоник. Результаты расчета показаны на рис. 3. Уравнения (3) положены в основу построения системы векторного управления асинхронным двигателем, которая промоделирована в пакете Matlab. На рис. 3 представлен результат расчета прямого пуска асинхронного двигателя, в цепи напряжения питания которого присутствуют первая и седьмая гармоники.
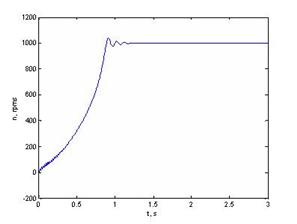
Выводы. Наличие седьмой гармоники в напряжении питания не оказывает существенного влияния на работу двигателя. Искусственное создание седьмой гармоники может быть использовано в дальнейших исследованиях. Так как модель на рис. 1 допустимо использовать при установившихся режимах, идет разработка расширенной системы уравнений Горева-Парка по образцу модели на рис. 2.