Муравьиные алгоритмы
Источник: http://soft.mail.ru/journal/pdfversions/32150.pdf
В последние годы интенсивно разрабатывается научное направление Natural Computing— «Природные вычисления», объединяющее математические методы, в которых заложены принципы природных механизмов принятия решений. Это механизмы обеспечивают эффективную адаптацию флоры и фауны к окружающей среде на протяжении миллионов лет. Имитация самоорганизации муравьиной колонии составляет основу муравьиных алгоритмов оптимизации— нового перспектив ного метода природных вычислений. Колония муравьев может рассматриваться как многоагентная система, в которой каждый агент (муравей) функционирует автономно по очень простым правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным.
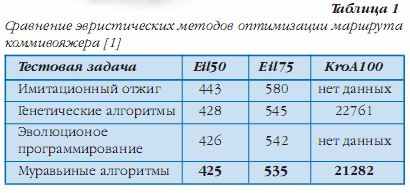
Муравьиные алгоритмы серьезно исследуются европейскими учеными с середины 90х годов. На сегодня уже получены хорошие результаты муравьиной оптимизации таких сложных комбинаторных задач, как: задачи коммивояжера, задачи оптимизации маршрутов грузовиков, задачи раскраски графа, квадратичной задачи о назначениях, оптимизации сетевых графиков, задачи календарного планирования и других. Особенно эффективны муравьиные алгоритмы при online оптимизации процессов в распределенных нестационарных системах, например трафиков в телекоммуникационных сетях.
Введение
В последние два десятилетия при оптимизации сложных систем исследователи все чаще при меняют природные механизмы поиска наилучших решений. Это механизмы обеспечивают эффективную адаптацию флоры и фауны к окружающей среде на протяжении миллионов лет. Сегодня интенсивно разрабатывается научное на правление Natural Computing— «Природные вычисления», объединяющее методы с природными механизмами принятия решений, а именно:
- Genetic Algorithms — генетические алгоритмы;
- Evolution Programming — эволюционное программирование;
- Neural Network Computing — нейросетевые вычисления;
- DNA Computing — ДНК вычисления;
- Cellular Automata — клеточные автоматы;
- Ant Colony Algorithms— муравьиные алгоритмы.
Целью настоящей статьи является изложение теоретических основ и примеров практического применения муравьиных алгоритмов — нового перспективного метода оптимизации, базирую щегося на моделировании поведения колонии муравьев. Колония муравьев может рассматри ваться как многоагентная система, в которой каж дый агент (муравей) функционирует автономно по очень простым правилам. В противовес почти примитивному поведению агентов, поведение всей системы получается на удивление разумным.
Муравьиные алгоритмы серьезно исследуют ся европейскими учеными с середины 90х годов На сегодня уже получены хорошие результаты муравьиной оптимизации таких сложных комби наторных задач, как: задачи коммивояжера, зада чи оптимизации маршрутов грузовиков, задачи раскраски графа, квадратичной задачи о назначе ниях, оптимизации сетевых графиков, задачи ка лендарного планирования и других. Несмотря на стремительные успехи муравьиных алгоритмов подавляющее большинство русскоязычных спе циалистов по исследованию операций не знако мы с этой технологией оптимизации.
Статья состоит из трех частей: в первой части излагается теория муравьиных алгоритмов, во второй — описывается решение муравьиными алгоритмами задачи о коммивояжере, в третьей части дается обзор применения муравьиных ал горитмов. Теоретическая часть статьи базируется на книгах [1, 2], лекции изобретателя муравьиных алгоритмов доктора Марко Дориго в летней шко ле по сложным системам [3] и материалах сайта [4].
Принципы поведения муравьев
Принципы поведения муравьев выдержали испытания далеко не в лабораторных условиях на протяжении 100 миллионов лет — именно столько времени назад муравьи «колонизирова ли» Землю. Муравьи относятся к социальным на секомым, живущим внутри некоторого коллекти ва— колонии. На Земле около двух процентов насекомых являются социальными, половину из них составляют муравьи — небольшие существа массой от 1 до 5 мг.
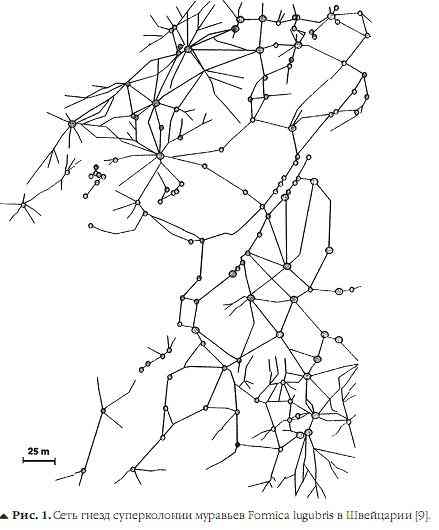
Число муравьев в одной колонии колеблется от 30 штук до нескольких миллионов. На Земле около 10+E16 муравьев с общей массой, приблизи тельно равной массе человечества. Поведение муравьев при транспортировании пищи, преодо лении препятствий, строительстве муравейника и других действиях зачастую приближается к тео ретически оптимальному. В качестве примера на рис. 1 приведена структура взаимосвязанных гнезд суперколонии муравьев Formica lugubris в Швейцарии. Сеть муравейников близка к мини мальному остовному дереву, соединяющему все гнезда колонии – вершины графа на рис. 1.
Какие же механизмы обеспечивают столь сложное поведение муравьев, и что можем мы позаимствовать у этих крошечных существ для решения своих глобальных задач? Основу «соци ального» поведения муравьев составляет самоор ганизация — множество динамических механиз мов, обеспечивающих достижение системой гло бальной цели в результате низкоуровневого вза имодействия ее элементов. Принципиальной особенностью такого взаимодействия является использование элементами системы только ло кальной информации. При этом исключается лю бое централизованное управление и обращение к глобальному образу, репрезентирующему сис тему во внешнем мире. Самоорганизация являет ся результатом взаимодействия следующих четы рех компонентов:
- случайность;
- многократность;
- положительная обратная связь;
- отрицательная обратная связь
Муравьи используют два способа передачи информации: прямой — обмен пищей, мандибу лярный, визуальный и химический контакты, и непрямой — стигмержи (stigmergy). Стигмержи — это разнесенный во времени тип взаимо действия, когда один субъект взаимодействия из меняет некоторую часть окружающей среды, а остальные используют информацию об ее состо янии позже, когда находятся в ее окрестности. Биологически стигмержи осуществляется через феромон (pheromone) — специальный секрет, от кладываемый как след при перемещении муравья. Феромон — достаточно стойкое вещество, он мо жет восприниматься муравьями несколько суток. Чем выше концентрация феромона на тропе, тем больше муравьев будет по ней двигаться. Со вре менем феромон испаряется, что позволяет мура вьям адаптировать свое поведение под изменения внешней среды. Распределение феромона по про странству передвижения муравьев является свое го рода динамически изменяемой глобальной па мятью муравейника. Любой муравей в фиксиро ванный момент времени может воспринимать и изменять лишь одну локальную ячейку этой гло бальной памяти.
Муравьиные алгоритмы основаны на имита ции природных механизмов самоорганизации муравьев, использование которых иллюстрирует ся в следующих разделах на примере оптимиза ции маршрута коммивояжера.
Муравьиная оптимизация маршрута коммивояжера
Ниже приводится муравьиный алгоритм опти мизации маршрута коммивояжера, реализующий все идеи предыдущего раздела (в угловых скобках содержится словесное описание соответствующе го кода).
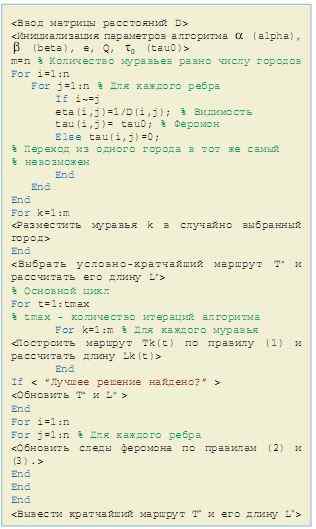
Муравьиный алгоритм был запрограммиро ван в системе MATLAB и протестирован на серии задач из библиотеки [5]. Для задачи с 29 населен ными пунктами в Баварии «Bays29» алгоритм без элитных муравьев после 100 итераций нашел оп тимальный маршрут длиной 2020 только в одном случае из пяти. Решение можно улучшить про стым увеличением количества итераций до 12 тысяч. Длины маршрутов муравьев на одной ите рации отличаются незначительно, поэтому для ускорения нахождения оптимума необходимо искусственно усиливать наилучшие текущие ре шения с помощью элитных муравьев. На рис. 2 показаны усредненные динамики решения задачи «Bays29» алгоритмами с различным числом элитных муравьев.
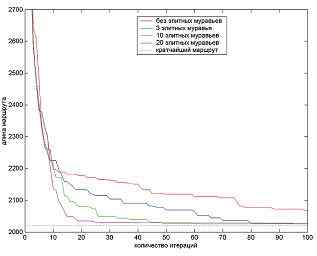
Рис. 2. Сравнение эффективности алгоритмов с разным числом элитных муравьев.
Эксперименты для каждого алгоритма повто рялись 5 раз. На первый взгляд кажется, что чем больше элитных муравьев, тем лучше работает алгоритм. Действительно, алгоритмы с большим количеством элитных муравьев очень быстро, за 3040 итераций находят субоптимальные марш руты длиной 2033, 2028, 2026, однако после это го надолго застревают в локальных оптимумах, т. к. элитные муравьи очень сильно усиливают эти субоптимальные решения. В пяти экспериментах за 100 итераций алгоритм с тремя элитными му равьями трижды нашел оптимальный маршрут, с десятью элитными муравьями — дважды, а с двад цатью — только один раз. Несмотря на то, что ал горитм с тремя элитными муравьями медленнее приближается к хорошим маршрутам, он намно го быстрее проходит субоптимальные решения ловушки.
Проведенные нами эксперименты свидетель ствуют, что популяция решений никогда не вы рождается к одному, общему для всех муравьев маршруту. Наоборот, алгоритм продолжает син тезировать новые, возможно лучшие решения. На рис. 3, а синей линией показаны наилучшие реше ния, найденные на каждой итерации алгоритма с тремя элитными муравьями. Красной линией по казаны наилучшие решения, найденные с начала работы алгоритма. Как видно, линии не совпадают, следовательно, муравьиный алгоритм генери рует новые решения на каждой итерации. Об этом свидетельствует и рис. 3, б, на котором показано среднеквадратическое отклонение длин маршрутов, найденных муравьями на текущей итерации алгоритма.

Рис. 3. Исследование процесса решения задачи коммивояжера муравьиным алгоритмом.
Даже если оптимальный маршрут уже найден, алгоритм продолжает поддерживать разнообраз ность популяции решений. На рис. 3, в показано среднее по городам число разветвлений следов феромона на текущей итерации алгоритма. Оно получено подсчетом ребер, инцидентных верши не графа, след феромона на которых превышает некоторый порог. Это число колеблется около 4–5 на протяжении всей работы алгоритма, следова тельно, в любом городе для муравья существует несколько перспективных альтернатив продолже ния маршрута. Эволюция маршрутов коммивоя жера, найденных алгоритмом с тремя элитными муравьями, показана на рис. 4.
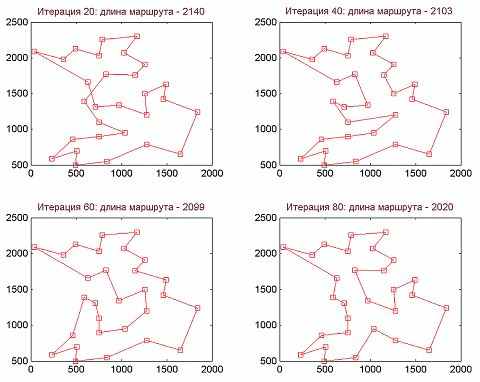
Рис. 4. Эволюция маршрутов коммивояжера для задачи «Bays29».
По сравнению с точными методами, например динамическим программированием или методом ветвей и границ, муравьиный алгоритм находит близкие к оптимуму решения за значительно меньшее время даже для задач небольшой размерности (n>=20). Время оптимизации муравьиным алгоритмом является полиномиальной функцией от размерности O(t, n*n, m), тогда как для точных методов зависимость экспоненциальная.
Обзор применения муравьиных алгоритмов оптимизации
Приведенный в статье муравьиный алгоритм оптимизации маршрута коммивояжера после незначительных модификаций может использо ваться для решения различных комбинаторных задач: квадратичной задачи о назначениях (Quadratic Assignment Problem), задачи об оптимизации маршрутов грузовиков (Vehicle Routing Problem), задачи календарного планирования (JobShop Schedule Planing), задачи раскраски графа (Graph Coloring Problem) и др. Муравьиные алгоритмы находят решения дискретных задач оптимизации не хуже других общих метаэвристи ческих технологий и некоторых проблемноориентированных методов.
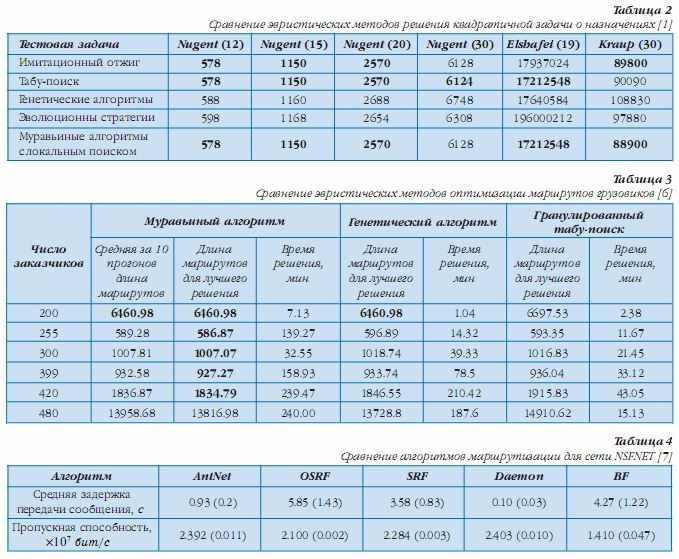
В табл. 1 приведены длины маршрутов коммивояжера, найденные различными эвристическими методами оптимизации. В табл. 2 сравниваются методы решения квадратичной задачи о назначениях. В ячейках таблицы указаны стоимости решений. В табл. 1 и 2 число в названии тестовой задачи указывает ее размерность. В табл. 3 сравниваются три метода оптимизации маршрутов грузовиков для задач большой размерности. Время решения задач пересчитано для компьютера с процессором Pentium900MHz. Во всех таблицах полужирным шрифтом выделены наилучшие на сегодняшний день решения.
Высокую эффективность муравьиные алгоритмы демонстрируют при оптимизации распределенных нестационарных систем. Ярким примером может служить нахождение муравьиными алгоритмами оптимальных трафиков в телекоммуникационных сетях [1, 7]. В качестве примера в табл. 4 приведены результаты маршрутизации в американской сети NSFNET, содержащей 14 узлов с 21 двунаправленной линией связи.
Сравнивались следующие алгоритмы: AntNet — муравьиный алгоритм; OSRF — официальный интернетовский алгоритм маршрутизации; SRF — алгоритм, использующий динамическую метрику при оценке стоимости соединений; Daemon — аппроксимация идеального алгоритма маршрутизации; BF— алгоритм Беллмана-Форда. В таблице приведены средние значения времени задержки и пропускной способности при интенсивной загрузке сети. Числа в скобках — значения среднеквадратических отклонений при 10 кратном прогоне алгоритмов. Детальную информацию об этих и других применениях муравьиных алгоритмов можно найти на сайтах [4, 8].
Выводы
Муравьиные алгоритмы основаны на имитации самоорганизации социальных насекомых посредством использования динамических механизмов, с помощью которых система достигает глобальной цели в результате локального низкоуровневого взаимодействия элементов. В статье на примере задачи коммивояжера показано, как в алгоритмы решения дискретных задач оптимизации внедрить составляющие самоорганизации муравьев: случайность, многократность взаимодействия, отрицательную и положительную обратные связи. Проведенные компьютерные эксперименты показывают, что муравьиные алгоритмы находят хорошие маршруты коммивояжера значительно быстрее, чем точные методы комбинаторной оптимизации. Эффективность муравьиных алгоритмов увеличивается с ростом размерности задачи оптимизации.
Муравьиные алгоритмы обеспечивают решения и других комбинаторных задач не хуже общих метаэвристические технологий оптимизации и некоторых проблемноориентированных методов. Особенно хорошие результаты муравьиной оптимизации получаются для нестационарных систем, параметры которых изменяются во времени, например телекоммуникационных и компьютерных сетей.
Важным свойством муравьиных алгоритмов является неконвергентность: даже после большого числа итераций одновременно исследуется множество вариантов решения, вследствие чего не происходит длительных временных задержек в локальных экстремумах. Все это позволяет рекомендовать применение муравьиных алгоритмов для решения сложных комбинаторных задач оптимизации. Перспективными путями улучшения муравьиных алгоритмов являются online адаптация параметров с помощью базы нечетких правил, а также их гибридизация с другими методами природных вычислений, например генетическими алгоритмами. Гибридизация может осуществляться по островной схеме, когда различные алгоритмы решают задачу параллельно и автономно (каждый на отдельном «острове») с обменом наилучшими решениями через определенное время, или по принципу «мастер–подмастерье», когда основной алгоритм — «мастер» передает решение типовых подзадач «подмастерью» — специализированному, быстрому алгоритму.
Литература
- Bonavear E., DorigoM. Swarm Intelligence: from Natural to Artificial Systems.— Oxford University Press, 1999.— 307 p.
- Corne D., Dorigo M., Glover F. New Ideas in Optimization.— McGravHill, 1999.
- Dorigo M. Swarm Intelligence, Ant Algorithms and Ant Colony Optimization // Reader for CEU Summer University Course «Complex System».— Budapest, Central European University, 2001.— P. 1–38.
- http://irida.ulb.ac.de/ACO/ACO.html
- http://www.iwr.uniheidelberg.de/iwr/comopt/soft/TSPLIB95/TSPLIB.html
- Reimann M. Ant Based Optimization in Good Transportation. PhD Thesis. University of Vienna. — Vienna, Austria, 2002. — 149 p.
- Caro G. D., DorigoM. Anet: a Mobile Agents Approach to Adaptive Routing. Technical Report IRIDA 9712. IRIDA — Universite Libre de Brusseles. — Brussels, Belgium, 1997. — 27 p.
- http://www.swarm.org
- Cherix D. Note preliminaire sur la structure, la phenologie et le regime alimentaire d'une supercolonie de Formica lugubris Zett. // Insects Sociaux 27, 1980.— P. 226–236.
