Исходя из параметрической теории систем, экономайзер, например, — энергетическая система, т.к. отношение (если изменился расход топлива, то изменилась температура питательной воды, например) определяет динамические свойства температуры питательной воды по данному каналу взаимодействия [1].
Диагностику как оценку состояния энергетических систем через контроль их работоспособности, т.е. проверку определения диагностируемого параметра в области допустимых значений (в допуске, не в допуске), рассматривают как протекающий в системе диагноза процесс многократной подачи в систему входных воздействий и многократное измерение и анализ ответов (выходных воздействий — реакций системы на поданные входные воздействия) [2].
Функциональная компьютерная диагностика, являющаяся непрерывным динамическим процессом оценки состояния энергетических систем, основана на применении экспертных систем, способных обрабатывать не только количественные данные, определяющие работоспособность систем, но и различного рода знания, позволяющие на основе проведения анализа диагностической информации принимать экспертные решения [3].
Основу функциональных диагностических мероприятий составляет математическое моделирование динамики энергетической системы относительно выбранных на основе экспертных знаний существенных диагностируемых параметров, являющихся определяющими при функционировании данной системы, например, температура рабочего тела на выходе из экономайзера, пароперегревателя, паросодержание рабочего тела на выходе из кипящего экономайзера, расход теплоносителя в отопительной сети, температура кипящего слоя и т.д.
Динамические процессы, протекающие в энергетической системе, описываются уравнениями неравновесной термодинамики [4, 5]. Разработку математической модели начинают с оценки физической модели системы, выраженной уравнением состояния. Так, например, уравнение состояния пароперегревателя, экономайзера определяют в виде
где r — плотность рабочего тела, кг/м3;
p — давление рабочего тела, МПа;
t — температура рабочего тела, К.
Для кипящего экономайзера необходимо дополнение этой функциональной связи еще одной независимой переменной — паросодержанием рабочего тела
где x — паросодержание рабочего тела.
Для топки с кипящим слоем, например, уравнение состояния определяет основополагающую физическую основу существования слоя
где Dp — перепад давления на кипящем слое, МПа;
t — температура кипящего слоя, К;
e — порозность слоя;
u — скорость газов, м/с.
Далее, разрабатывая математическую модель, уравнение состояния дополняют уравнениями энергии передающей и воспринимающей сред, которые рассматривают как уравнения переноса энтальпии. Уравнение энергии воспринимающей среды, характеризующееся наличием существенного диагностируемого параметра, например, температуры, паросодержания рабочего тела, составляют относительно этого параметра, представляя его изменение не только во времени, но и вдоль пространственной координаты оси теплообменника, совпадающей с направлением движения потока среды.
Для изменения температуры рабочего тела в экономайзере, пароперегревателе как существенных диагностируемых параметров уравнение энергии приобретает вид
 |
где
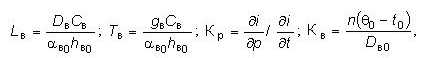 |
i — энтальпия рабочего тела, кДж/кг;
a — коэффициент теплоотдачи, кВт/м2К;
C — удельная теплоемкость, кДж/кгК;
D — расход вещества, кг/с;
g — удельная масса вещества, кг/м;
h — удельная поверхность, м2/м;
t — температура рабочего тела, К;
q — температура разделяющей стенки, К;
t — время, с;
z — координата длины теплообменника, м;
Tв — постоянная времени, характеризующая тепловую аккумулирующую способность рабочего тела, с;
n — показатель зависимости коэффициента теплоотдачи от расхода.
Индексы: 0 — исходный стационарный режим; в — внутренний поток.
Например, полагая паросодержание рабочего тела в качестве определяющего параметра, представляют его изменение во времени и вдоль пространственной координаты в уравнении энергии рабочего тела следующим образом:
 |
где
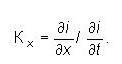 |
Если в качестве существенного диагностируемого параметра выбран расход рабочего тела, разрабатывая математическую модель динамики как основы диагностики, уравнение энергии дополняют уравнением сплошности рабочей среды, которое, например, для кипящего экономайзера может быть представлено в виде
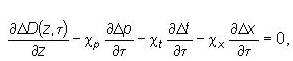 |
где
 |
f — сечение для прохода рабочего тела, м2.
Затем полученное уравнение энергии и, при необходимости, с использованием уравнения сплошности решают совместно с уравнениями энергии газов и теплового баланса стенки.
Уравнение энергии газов
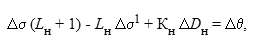 |
где
s — температура газов, К;
Индексы: 1 — вход в теплообменник; н — наружный поток.
Уравнение теплового баланса стенки
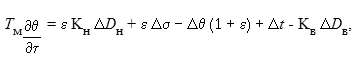 |
где
 |
Tм — постоянная времени, характеризующая тепловую аккумулирующую способность металла, с;
m — показатель зависимости коэффициента теплоотдачи от расхода.
Индекс: м — металлическая стенка.
Для топки с кипящим слоем температуру кипящего слоя как существенный диагностируемый параметр рассматривают в уравнении энергии передающего потока, т.е. в уравнении энергии слоя
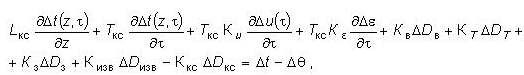 |
где
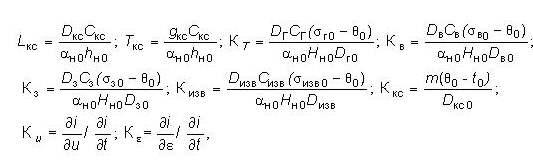 |
i — энтальпия газов, кДж/кг;
H — полная поверхность, м2;
t — температура кипящего слоя, К;
Tкс — постоянная времени, характеризующая тепловую аккумулирующую способность кипящего слоя, с.
Индексы: кс, г, т, в, изв, з — кипящий слой, газы, топливо, воздух, известняк, зола.
Затем полученное уравнение энергии кипящего слоя дополняют уравнениями энергии рабочего тела и теплового баланса стенки.
Уравнение энергии рабочего тела для погруженного в кипящий слой теплообменника имеет вид
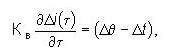 |
Уравнение теплового баланса стенки
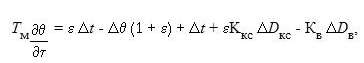 |
где
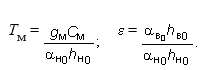 |
Отличительной особенностью диагностических моделей являются уравнения энергии, разработанные относительно существенных диагностируемых параметров. Именно они содержат члены, отражающие широкий спектр возмущающих воздействий, поступающих на вход функционирующей энергетической системы со стороны окружающей среды. Изменения расхода топлива, питательной воды, нагрузки, воздуха и т.д. и создают информационную основу диагностических мероприятий.
Контроль работоспособности энергетических систем на основе реализованной нелинейной математической модели осуществляют с использованием графа причинно-следственных связей [3].
Предложенное обоснование математического моделирования динамики энергетических систем как основы диагностики, подтвержденное результатами разработанных и реализованных моделей [6, 7], может быть использовано для проведения широкого спектра диагностических мероприятий в процессе функционирования энергетических систем.
Литература
1. Уемов А.И. Системный подход и общая теория систем. - М.: Мысль, 1978.
2.Пархоменко П.П., Согомонян Е.С. Основы технической диагностики. - М.: Энергия, 1976.
3. Чайковская Е.Е. Динамическая подсистема как основа экспертных систем // Тр. Одес. политехн. ун-та. - Одесса, 1999. - Вып. 3(9). - С. 108 - 110.
4. Гроот С., Мазур П. Неравновесная термодинамика. - М.: Мир, 1964.
5. Серов Е.П., Корольков Б.П. Динамика парогенераторов. - М.: Энергия, 1972.
6. Чайковская Е.Е. Параметрическая диагностика динамики температуры кипящего слоя // Энергетика и электрификация. - 1999. - № 1. - С. 4 - 7.
7. Чайковская Е.Е. Влияние кипящего экономайзера на инерционность участка питания котла // Изв. вузов. Энергетика. - 1991. - № 3. - С. 4 - 7.