Источник: Cборник научных трудов по материалам Международной научной конференции «Теоретические и практические аспекты научных исследований» Часть 1

Технические науки

Приборы и методы контроля и определения состава веществ

Применение люминесцентного метода для измерения концентрации растворенного кислорода в сточных водах

Рассмотрена теория тушения флуоресценции, сформулировано основное требование тушения. Подробно описано уравнение, согласно которому происходит динамическое тушение – уравнение Штерна-Фольмера. Показана зависимость интенсивности тушения от температуры.

Ключевые слова: растворенный кислород, люминесцентный метод, флуорофор, тушение флуоресценции.

Розглянуто теорію гасіння флуоресценції, сформульовано основну вимогу гасіння. Докладно описано рівняння, згідно з яким відбувається динамічне гасіння – рівняння Штерна-Фольмера. Показана залежність інтенсивності гасіння від температури.

Ключові слова: розчинений кисень, люмінесцентний метод, флуорофор, гасіння флуоресценції.

In the article the theory of fluorescence quenching is considered and basic requirement of extinction is formulated. The equation, according to which there is a dynamic quenching, is described in detail. It is called Stern-Volmer equation. The dependence of intensity from temperature is shown.

Keywords: dissolved oxygen, luminescence method, fluorophore, fluorescence quenching.

Прокофьева Елена Викторовна

Донецкий национальный технический университет

Постановка задачи. На сегодняшний день проблема очистки сточных вод является весьма актуальной, так как вода является ценным природным ресурсом. Наиболее эффективной является биологическая очистка сточных вод. В процессе очистки происходит аэрация активного ила, на что затрачивается значительная часть энергии, потребляемой очистными сооружениями. С целью экономии энергии при аэрации необходимо постоянно контролировать концентрации растворенного в иле кислорода. Основной недостаток существующих датчиков измерения концентрации растворенного кислорода, основанных на электрохимическом методе, состоит в их нестабильности и дрейфе показаний при выполнении продолжительных измерений. Это происходит из-за того, что для каждой восстановленной на катоде молекулы имеет место соответствующая окислительная реакция на аноде, которая ведет к разрушению анода и изменению концентрации рабочего электролита. Поэтому необходимо применение другого более точного метода, каким является флуоресцентный метод измерения.

Исследования. Люминесцентные методы исследования с каждым годом находят все более широкое применение в химии, биологии, медицине, различных областях техники. Эти методы обладают исключительно высокой чувствительностью и дают уникальные возможности изучения возбужденных состояний молекул, фотохимических реакций, динамики быстрых молекулярных процессов, структуры и свойств сложных химических и биологических объектов.

Флуоресцентный метод, являющийся разновидностью люминесцентного, характеризуется высокой чувствительностью. Для измерения концентрации растворенного кислорода можно воспользоваться флуоресцентным методом. Флуоресцентный метод измерения концентрации кислорода в некоторой среде базируется на зависимости интенсивности тушения флуоресценции некоторого красителя, помещенного в среду, от концентрации кислорода в этой среде. В качестве красителей (флуорофоров), обладающих флуоресценцией могут быть применены полимерные композиции на основе полиароматических красителей, например, пирена или декациклена, а также на основе флуоресцирующих комплексов рутения (Ru(bpy)3, Ru(phen)3, так же можно применять фосфоресцирующие красители порфириновой природы Pt- и Pd-комплексы порфиринов [1]. Одним из наиболее известных динамических тушителей является молекулярный кислород [2]. Концентрация кислорода определяется по длительности (или времени жизни) процесса тушения флуоресценции.

Тушением флуоресценции называют любые процессы, которые уменьшают интенсивность флуоресценции использованного флуоресцирующего красителя. К тушению может приводить множество процессов, таких как: а) реакции в возбужденном состоянии, б) перенос энергии, в) образование комплексов, г) тушение при столкновениях. Для измерения концентрации растворенного кислорода используется тушение, связанное со случайными столкновениями между флуорофором и тушителем (кислородом), называется динамическим, или тушением при столкновениях.

Для тушения требуется контакт между молекулами флуорофора и тушителя (кислорода). В случае динамического тушения тушитель (кислород) должен диффундировать к флуорофору в течение времени нахождения в возбужденном состоянии. В результате контакта флуорофор возвращается в основное состояние без излучения фотона (рисунок 1).

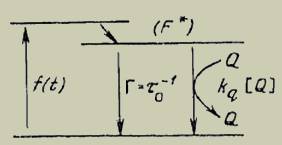
Рисунок 1 – Схема динамического тушения флуоресценции

На рисунке 1, ƒ(t) – постоянная функция возбуждения флуоресценции, Г=τ₀^-1 константа скорости дезактивации флуорофора в отсутствие тушителя, F^* – интенсивность флуоресценции в возбужденном состоянии, k_q – бимолекулярная константа скорости тушения.

Основным требованием тушения является контакт флуорофора и тушителя, то есть необходим контакт между молекулами кислорода и флуорофора. Так же для динамического тушения важным является увеличение объемов и расстояний в растворе (воде), влияющих на экспериментальные данные, которыми являются интенсивность или время затухания флуоресценции. Среднеквадратичное смещение (Δx²)^½ на которое тушитель (кислород) может продиффундировать за время жизни возбужденного состояния τ, составляет Δx²=2·D·τ, где D – коэффициент диффузии. Рассмотрим молекулу кислорода в воде при 25 °С (D=2,5 · 10^-5 см²/с). В течение типичного времени затухания флуоресценции (4 нc) молекула кислорода может продиффундировать на 44 Å. Если время затухания длительнее, может наблюдаться диффузия на еще большие расстояния. Например, для времен затухания 20 и 100 нс средние расстояния диффузии кислорода составляют 100 и 224 Å соответственно. Так как одного диффузионного столкновения с кислородом достаточно для тушения большинства флуорофоров, измерение тушения флуоресценции выявляет диффузию тушителей на сравнительно больших расстояниях.

Динамическое тушение флуоресценции описывается уравнением Штерна-Фольмера:

где F₀ и F – интенсивности флуоресценции в отсутствие и в присутствии тушителя соответственно; k_q – бимолекулярная константа скорости тушения; τ₀ – время затухания флуоресценции в отсутствие тушителя; [Q] – концентрация тушителя; k_дин=k_q·τ₀ – штерн-фольмеровская константа тушения.

Данные по тушению обычно представляют в координатах F₀/F от [Q], поскольку F₀/F, как ожидается, должно линейно зависеть от концентрации тушителя. График дает отсекаемый отрезок на оси у, равный единице, и наклон, равный k_дин (рисунок 2). Полезно отметить, что k_дин^-1 равна концентрации тушителя, при которой F₀/F=2, т.е. тушится 50% интенсивности флуоресценции. Прямолинейная зависимость в координатах Штерна-Фольмера указывает на существование в растворе одного типа флуорофора доступного для тушителя. Если присутствуют два типа флуорофоров и один из них недоступен для тушителя, то штерн-фольмеровский график отклоняется от линейности в сторону оси х.

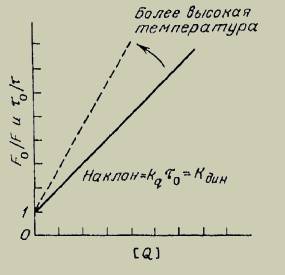
Рисунок 2 – График динамического тушения флуоресценции в координатах Штерна-Фольмера

Согласно рисунку 2, повышение температуры приводит к изменению наклона прямой (зависимости отношения интенсивности флуоресценции в отсутствие и в присутствии тушителя либо зависимости отношения времени затухания флуоресценции в отсутствие и в присутствии тушителя к концентрации тушителя (кислорода)), то есть к увеличению k_дин.

Вывод уравнения Штерна-Фольмера. Уравнение Штерна-Фольмера может быть выведено несколькими способами. Рассмотрим интенсивность флуоресценции в отсутствие и в присутствии тушителя. Интенсивность флуоресценции, наблюдаемая для флуорофора, пропорциональна его концентрации в возбужденном состоянии F^*. При непрерывном облучении устанавливается стационарная концентрация возбужденных флуорофоров и, следовательно, d[F^*]/dt=0, В отсутствие и в присутствии тушителя дифференциальные уравнения, описывающие F^*, представляются в виде

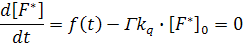
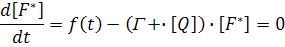
где ƒ(t) – постоянная функция возбуждения флуоресценции, которая легко исключается из этих уравнений, Г=τ₀^-1 представляет собой константу скорости дезактивации флуорофора в отсутствие тушителя. Из уравнений (2) и (3) получаем уравнение Штерна-Фольмера

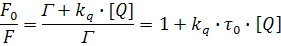
Это уравнение может быть также выведено путем рассмотрения доли возбужденных флуорофоров, дезактивирующихся путем излучения, по отношению к общему числу возбужденных флуорофоров. Доля F₀/F определяется отношением скорости затухания Г флуоресценции к общей скорости затухания в присутствии тушителя (Г+k_q·[Q]):

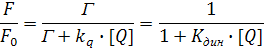
Это выражение также является уравнением Штерна-Фольмера.

Так как динамическое тушение является конкурирующим процессом, который дезактивирует возбужденное состояние, время затухания в отсутствие τ₀ и в присутствии τ тушителя представляется выражениями

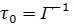
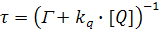
и, следовательно

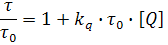
Последний вывод иллюстрирует важную характеристику динамического тушения, которая состоит в одинаковом уменьшении интенсивности и времени затухания флуоресценции (рисунок 2):

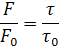
Уменьшение времени затухания происходит из-за того, что тушение представляет собой дополнительный конкурирующий процесс, дезактивирующий возбужденное состояние без испускания флуоресценции, что ведет к уменьшению квантового выхода. Благодаря этим ценным свойствам тушение при столкновениях используют для контроля времени затухания с последующим определением природы наносекундной кинетики затухания анизотропии или временной зависимости релаксации растворителя.

Интерпретация бимолекулярной константы скорости тушения, входящей в уравнение Штерна-Фольмера. Частота столкновений флуорофора с тушителем представляется выражением

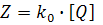
где k₀ – диффузионно-контролируемая бимолекулярная константа скорости, которая может быть вычислена по уравнению Смолуховского:

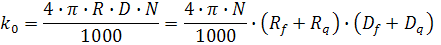
где R – радиус столкновения; D – сумма коэффициентов диффузии флуорофора D_f и тушителя D_q, N – число Авогадро. Радиус столкновения обычно принимается равным сумме молекулярных радиусов флуорофора R_f и тушителя R_q. Уравнение описывает диффузионный поток молекул с коэффициентом диффузии D через поверхность сферы радиуса R. Фактор 1000 необходим для соблюдения размерности в тех случаях, когда концентрация выражена в молях на литр: умножением на (N/1000) молярность пересчитывают в молекулы/см³.

Частота столкновений связана с бимолекулярной константой скорости тушения через эффективность тушения γ:

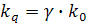
У тушителей, подобных кислороду, эффективность обычно близка к единице [3].

Эффективность тушения может быть рассчитана на основе наблюдаемого значения k_q, если известны коэффициенты диффузии и молекулярные радиусы. Радиусы можно найти из молекулярных моделей или молекулярных масс и плотностей исследуемых веществ. Коэффициенты диффузии можно вычислить но уравнению Стокса-Эйнштейна:

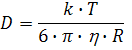
где k – константа Больцмана; η – вязкость растворителя. Часто при расчетах по уравнению Стокса-Эйнштейна недооцениваются коэффициенты диффузии малых молекул. Коэффициенты диффузии можно также получить из номограмм, основанных на термодинамических и физических свойствах систем [4]. Если коэффициенты диффузии известны, то бимолекулярную константу скорости тушения для γ=1 можно предсказать, используя уравнение Смолуховского (11).

При 25°С коэффициент диффузии кислорода в воде составляет 2,5 · 10^-5 см²/с. Если принять радиус столкновения равным 5 А, то подстановка в уравнение (11) дает k₀=1.2 · 10¹⁰ М^-1 · с^-1. Наблюдаемое значение константы Штерна-Фольмера для тушения кислородом составляет 32,5 М^-1. Бимолекулярная константа скорости тушения порядка 1 · 10¹⁰ М^-1 · с^-1 может рассматриваться как наибольшее из возможных значений для водных растворов.

Динамическое тушение зависит от диффузии. Поскольку повышение температуры приводит к увеличению коэффициентов диффузии, можно ожидать, что бимолекулярная константа скорости тушения возрастет с увеличением температуры (рисунок 2). Точнее, следует ожидать, что k_q будет пропорциональна Т/η, так как коэффициенты диффузии пропорциональны этому отношению уравнение (13).

Динамическое тушение влияет только на возбужденные состояния флуорофоров, и можно полагать, что оно не изменит спектры поглощения.

Молекулярный радиус для кислорода 2 Å.

Уравнение Смолуховского. Скорость диффузионно-контролируемой реакции, в которой лимитирующей стадией является частота столкновений реагентов, представлена выражением

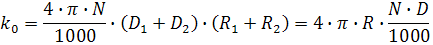
D_i и R_i – коэффициенты диффузии и молекулярные радиусы диффундирующих веществ; D и R – суммы этих величин. Одно вещество можно рассматривать неподвижным, а второе – диффундирующим с коэффициентом диффузии D. Это уравнение часто интуитивно объясняют как поток диффундирующего вещества через поверхность сферы радиуса R, непосредственно после чего следует тушение. Это описание вызывает некоторую путаницу, так как диффузионный поток через поверхность пропорционален площади этой поверхности и D. Площадь поверхности сферы равна 4·π·R², но не 4·π·R, в то время как в уравнении (14) содержится член 4·π·R, но не 4·π·R². По-видимому, более подходящее объяснение этого расхождения приведено ниже.

Если в растворе молекулы тушителя распределены неравномерно, то возникает поток из более концентрированной в менее концентрированную область раствора. Поток J (моль/с) равен

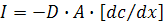
где А – площадь (см²); D – коэффициент диффузии (cм²/с); dc/dx – градиент концентраций [моль/см⁴ = моль/(см³·см)].

Частота столкновений Z флуорофора с тушителем может быть приравнена потоку тушителя через сферу радиуса R:

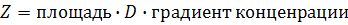
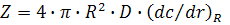
где 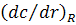– градиент концентрации на расстоянии R между флуорофором и тушителем. По уравнению Смолуховского 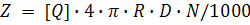и, таким образом,

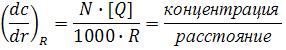
Величина(N[Q]/1000 – это число молекул в 1 см³, a R – расстояние. Следовательно, эффективный градиент концентраций, вызывающий тушение при столкновениях, определяется объемной концентрацией, деленной на R, это эквивалентно тому, что в центре флуорофора не может быть тушителя. Флуорофоры, которые соседствуют с тушителями, не флуоресцируют и не наблюдаются; следовательно, уравнение (18) описывает эффективный градиент вокруг непотушенных наблюдающихся флуорофоров. Исчезновение зависимости от R² в уравнении Смолуховского является результатом зависимости градиента концентрации от R^-1. Подробности приведены в работе [5].

Выводы. Таким образом, можно сделать вывод о том, что для измерения концентрации растворенного кислорода в сточных водах важно применять метод который дает достоверные результаты и требует наименьших затрат на его обслуживание, таким методом является люминесцентный. Так как датчики, основанные на электрохимическом методе измерения, нуждаются в постоянном обслуживании (очистке, калибровке, замене мембраны и электролита, полировки анода). В данной работе приведено уравнение, согласно которому происходит тушение флуоресценции, показано, что изменение температуры ведет к изменению штерн-фольмеровской константы. При повышении температуры увеличивается k_дин

Список использованных источников:

1. Папковский Д.Б.; Пономарев Г.В.; Курочкин И.Н.; Чернов С.Ф. Металлокомпелексы порфирин-кетонов, чувствительный элемент для определения кислорода в жидкой или газовой среде и способ определения кислорода. Патент РФ № 5055439/04, 1996

2. Kautsky H., Quenching of luminescence by oxygen, Trans. Faraday Soc., 35, 216 (1939).

3. Othmer D.F., Thakar M.S., Correlating diffusion coefficient in liquids, Ind. Eng. Chem., 45, 589 (1953).

4. Ware W,R., Oxygen quenching of fluorescence in solution: An experimental study of the diffusion process, J. Phys. Chem., 66, 455 (1962).

5. Collins F.C., Kimball G.E., Diffusion-controlled reaction rates, J. Colloid. Sci., 4, 425 (1949).