Источник: С.С. Замай, О.Э. Якубайлик. Модели оценки и прогноза загрязнения атмосферы промышленными выбросами в информационно-аналитической системе природоохранных служб крупного города: Учеб. пособие / Краснояр. гос. ун-т. Красноярск, 1998. с. 18-31

Значительное количество теоретических и экспериментальных работ посвящено дисперсии загрязняющих веществ, выбрасываемых в атмосферу. В настоящем учебном пособии будут в основном представлены математические модели, используемые для описания поведения выбросов в атмосфере на расстоянии по ветру до 10-20 км от источника.

Для больших расстояний представленные ниже методы считаются менее приемлемыми. По мере увеличения расстояния масштабы распространения выброса в вертикальном направлении становятся сравнимыми с толщиной планетарного пограничного слоя, и обычные предположения об однородности не позволяют использовать упрощенные модель. Кроме того, ниже описаны условия, при которых эти модели применимы, а также видоизменения моделей, необходимые для применения в конкретных практических ситуациях, и метеорологические данные, используемые в этих моделях.

Особенно важно учитывать ограничения этих моделей. Модели используемые в разных странах в качестве государственных, в основном применимы к ситуациям, в которых метеорологические параметры, такие как характеристики ветров и вертикальный градиент температуры, приблизительно равномерны во времени и пространстве.

Специально отметим, что в реальности могут возникнуть ситуации, в которых метеорологические параметры быстро изменяются во времени или пространстве. Общих моделей, которые бы охватывали все ситуации, не существует.

Поведение потока, выбрасываемого в атмосферу

После того, как примеси (радиоактивный или токсичный газ или аэрозоль) попадают в воздух, характер их перемещения и дисперсии определяется их собственными физическими свойствами и свойствами атмосферы, в которых они находятся. Для того чтобы наглядно показать характер их поведения, полезно рассмотреть поведение потока в целом после его попадания в атмосферу (см. рис.1). Выбросы проникают в атмосферу с определенной скоростью и температурой, которые обычно отличаются от соответствующих характеристик окружающей среды. Движение выбросов имеет вертикальную составляющую, обусловленную начальной вертикальной скоростью потока и разницей температур, до тех пор, пока не исчезнет воздействие этих факторов. Этот вертикальный подъем выбросов называют подъемом шлейфа. Он приводит к изменению эффективной высоты H точки выброса. На путь распространения выброса воздействуют также изменения потоков вблизи таких препятствий, как здания и сооружения.

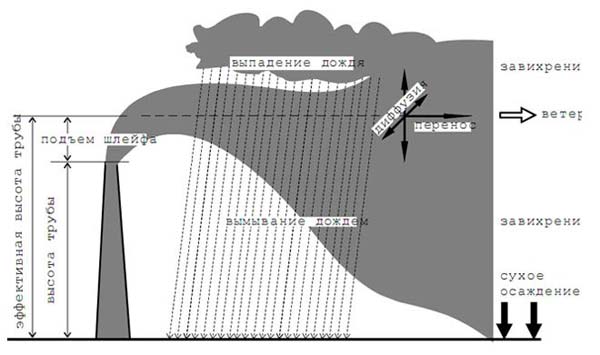
Рисунок 1 - Поведение загрязняющих веществ, выброшенных в атмосферу

Следуя руководству [1,2], мы будем использовать следующую терминологию.

Движение потока под действием ветра в течение и после подъема шлейфа называется переносом.

Турбулентное движение атмосферы вызывает произвольное движение выброса, приводящее к его распространению в горизонтальном и вертикальном направлениях за счет смещения с воздухом. Этот процесс называется атмосферной диффузией.

Комбинация переноса и диффузии называется атмосферной дисперсией. Модели, описывающие эти процессы, называют моделями атмосферного переноса - диффузии или моделями атмосферной дисперсии.

Выброс на стадии подъема шлейфа, переноса и диффузии может также испытывать воздействие таких процессов, как:

1. Химическая трансформация примесей;
2. Радиоактивный распад и накопление дочерних продуктов;
3. Влажное осаждение:
• дождь или снег (пар или аэрозоль попадают в капли воды или снежинки в облаке и выпадают в виде осадков);
• вымывание (пар или аэрозоль захватываются ниже дождевого облака падающими осадками);
• туман (пар или аэрозоль попадают в капли воды в тумане);
4. Сухое осаждение:
• седиментация аэрозолей или гравитационное осаждение (для частиц с диаметром более 10 мкм);
• отложение аэрозолей и адсорбция паров и газов на предметах, находящихся на пути ветра;
5. Образование и слипание аэрозолей.

Большую часть этих эффектов можно описать математически и при необходимости включить в математические модели. Отметим, что строгих указаний на эти модели в гостированных (имеющих официальный государственный статус) методиках нет. Это фактически означает, что разработчики должны исходить из конкретной ситуации и использовать адекватные ей модели.

Показатели турбулентности

При использовании моделей атмосферной дисперсии стабильность атмосферы необходимо выразить в следующих метеорологических параметрах или как их функцию переменных, перечень которых и пояснения к нему приведены ниже.

Вертикальный градиент температуры. Вертикальный градиент температуры является показателем скорости понижения температуры окружающей атмосферы в зависимости от высоты. Он равен -(dZ/dT), где Т – температура в градусах Кельвина, Z - высота над поверхностью земли.

Колебания направления ветра. Масштабы и периодичность колебаний направления ветра являются функциями интенсивности турбулентности (размера вихрей и т.д.). Поэтому на практике этот параметр используют для описания стабильности атмосферы. Среднее квадратичное отклонение колебаний направления ветра определяют с помощью электронной аппаратуры. Эти колебания могут быть обнаружены также в записях о направлении ветра, которые имеют различную ширину графических кривых для различных условий стабильности.

Инсоляция, облачность и скорость ветра. Тепловая турбулентность связана с тепловым потоком. Облачный покров уменьшает или увеличивает потери тепла, способствуя образованию нейтральной устойчивости. Сильные ветры, вызывающие усиленное перемешивание, также способствуют образованию нейтральной устойчивости. Ночью при ясном небе и слабом ветре атмосфера становится устойчивой, в то время как аналогичные условия в дневное время приводят к неустойчивости атмосферы. В дневное время целесообразно проводить измерения или оценки солнечной радиации для определения классов устойчивости, в ночных условиях можно использовать радиометры полного излучения; использование радиометров полного излучения может оказаться предпочтительным и в дневное время, когда коэффициент альбедо коротких волн имеет большую величину.

Число Ричардсона – Ri. Это число выражает соотношение тепловой, или конвективной, турбулентности и механической турбулентности. Оно зависит от высоты и является безразмерным параметром, определяемым формулой:

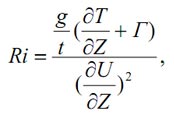
где g – ускорение силы тяжести (м \ c^-2);

T – температура (K);

Г – адиабатический вертикальный градиент (К× м^-1);

U – средняя скорость ветра (м \ c^-2);

Z – высота над уровнем земли (м).

Это число является одним из основных параметров, учитываемых в ряде экспериментов по атмосферной дисперсии. Однако, как правило, для измерения (∂Z/∂U) требуется точная и чувствительная аппаратура, поэтому расчет Ri общепринятым методом может оказаться затруднительным.

Объемное число Ричардсона Ri_B. Оно определяется по формуле:

где U_Z - скорость ветра на среднегеометрической точке высот, на которых замерялась температура для получения температурного профиля. Параметр Ri_B измеряется проще, чем Ri, поскольку для его определения не требуется знания градиентов скорости ветра. На практике U_Z можно определить с помощью анемометра, установленного на метеорологической башне.

Характеристики источников выбросов

При расчетах атмосферной дисперсии различные источники обычно классифицируют по их пространственной конфигурации и продолжительности выброса. К представляющим интерес пространственным конфигурациям источников относятся точечные, линейные, поверхностные и объемные. Линейные и поверхностные источники можно рассматривать как определенный набор эффективных точечных источников. На практике источники выбросов не являются точечными источниками в строгом смысле этого слова, но для упрощения математического описания их можно считать таковыми.

В зависимости от продолжительности выбросы могут быть: быстротечными (длительностью от нескольких секунд до нескольких минут при времени перемещения, равном нескольким часам), краткосрочными (длительностью до нескольких часов) и непрерывными.

Мы будем рассматривать краткосрочные и непрерывные выбросы.

Методы оценки дисперсии

Общий порядок оценки концентрации атмосферного загрязнения и/или дисперсии для данной площадки в течение как длительных, так и коротких периодов времени включает в себя:

• выбор соответствующей модели с учетом неровности рельефа местности и высоты выброса для данной площадки и ситуации;
• определение классов устойчивости (турбулентности) для конкретных условий с помощью соответствующих измеренных или визуально полученных параметров;
• определение скорости ветра на нужном уровне (обычно на уровне выброса) с помощью измерений на этом уровне или путем расчета с использованием логарифмических соотношений или соотношений функции мощности, в зависимости от измерений на других уровнях;
• определение эффективной высоты выброса с помощью выражений для подъема шлейфа;
• определение коэффициентов турбулентности на заданном расстоянии из графиков или формул в соответствии с моделью, которую можно выбрать в справочной литературе, например [1,2];
• расчет концентраций и коэффициентов дисперсии по соответствующим формулам.

В некоторых случаях для оценки дисперсии можно использовать упрощенные методы. Может оказаться возможным использовать уравнения, основанные на предположении о гомогенности характеристик атмосферной дисперсии в данном районе. Это особенно полезно, когда отсутствует конкретная метеорологическая информация о площадке, а сравнения с другими параметрами, такими как распределение населения (предварительное изыскание площадки), еще предстоит сделать, или когда речь идет только о незначительных выбросах.

Даже при использовании сложных методов, хотя и известно, что концентрации более или менее связаны с различными показателями устойчивости, имеется очень мало информации по разбросу результатов в пределах конкретного класса устойчивости.

Существует множество теоретических формул для расчета атмосферной дисперсии. Наиболее общее выражение для концентрации при наличии постоянного точечного источника мощностью Q без помех от земной поверхности при средней скорости ветра U, измеряемой на уровне шлейфа, получаем из предположения двойного распределения в уравнении Гаусса:

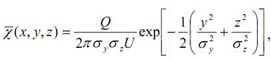
где χ – средняя концентрация выброса в точке (x, y, z), Q – мощность источника, U – скорость ветра, усредненная по слою перемешивания.

Для уравнения Гаусса начало координат находится в источнике. Ось x совпадает со средним направлением ветра. Ось y расположена перпендикулярно направлению ветра по горизонтали, а ось z – по вертикали. Параметры σ_y и σ_z представляют собой стандартные отклонения распределений концентраций в точке x соответственно в горизонтальном и вертикальном направлениях, перпендикулярно направлению ветра. Полная система координат приведена на рис. 3, мы будем придерживаться ее и в дальнейшем.

Рисунок 3 – Изображение системы координат и параметров дисперсии

Уравнении Гаусса предполагает шлейф с осью в виде прямой линии в направлении ветра, и не учитывает пространственно-временные изменения направления ветра. Его можно также использовать и для отличной от прямой линии траектории шлейфа при условии, что ее кривизна не слишком велика.

Параметры σ_y и σ_z в уравнении Гаусса увеличиваются с расстоянием x. Скорость их увеличения с расстоянием зависит от интенсивности турбулентности и тем самым от стабильности атмосферы. Для практического использования зависимости для σ_y и σ_z расстояния были определены на основании экспериментальных данных в различных полевых условиях.

Важно иметь в виду, что выражение Гаусса – всего лишь приближение. На практике можно встретить отклонения от этого приближения, особенно в вертикальном направлении (z) при сильном порывистом ветре и на больших расстояниях. Тем не менее, оно является удобной предпосылкой для использования в основном уравнении Гаусса.

Перечень основных моделей, используемых для оценки загрязнения атмосферы

Количество и характер моделей определяют, с одной стороны, кругом задач, стоящих перед экологическими службами, а с другой – требованиями к точности моделирования. Разнообразие требований к характеру оценок загрязнения и высокая специфичность распространения выбросов примесей в различных метеоусловиях приводят к необходимости использования тех моделей, которые перечислены ниже.

1. Штатные модели служб ГО. Стандартная методика основана на эмпирических моделях и позволяет определить максимально возможную зону поражения при выбросах ядовитых веществ. Модель указывает не реальное положение облака выбросов в тот или иной момент времени, а обозначает границы, в пределах которых концентрация ядовитых веществ может достичь опасных для здоровья человека значений при неблагоприятных метеоусловиях. Модель проста и быстро работает.
2. Стандартные модели загрязнения атмосферы стационарными источниками, основанные на модели ОНД-86. Модели могут быть использованы для анализа квазистационарных процессов, когда характерные времена выбросов токсичных веществ превышают характерные времена перемещения воздушных масс в экспертируемой области пространства (например, случаи пожаров или утечек на продуктопроводах). Модель эмпирическая и позволяет рассчитать установившееся распределение концентраций токсиканта при заданном ветре и максимально неблагоприятном с точки зрения рассеяния примесей состоянии атмосферы.
3. Модели МАГАТЭ (международный стандарт) для расчетов загрязнений атмосферы, создаваемых стационарными источниками примесей. Это наиболее полные из существующих в настоящее время эмпирических моделей. Характер их детализации позволяет учитывать особенности местных метеорологических условий и производить расчеты распределений концентрации примесей в текущих метеоусловиях. Модели требуют значительных работ по привязке к местным условиям. Время вычислений по моделям 2 и 3 практически одинаково.
4. Простейшие нестационарные модели для расчета распространения облака загрязняющих веществ, предназначенные для эксресс-прогноза. Модели строятся на основе методик и моделей МАГАТЭ и позволяют рассчитать траекторию и время движения облака выбросов до потери токсичности или в интересующей области в текущих метеоусловиях. Установившихся стандартов на такие модели нет.
5. Нестационарные модели загрязнения, учитывающие неоднородность подстилающей поверхности. Квазитрехмерные модели, основанные на использовании полуэмпирических моделей МАГАТЭ с решением уравнения переноса-диффузии примесей в приземном слое. Для повышения скорости и точности вычислений использованы высокоэффективные численные методы и учтена специфика решаемой задачи. Используются в случаях, когда необходимо учесть неоднородность подстилающей поверхности, а вычислительные ресурсы и/или недостаток информации не позволяют использовать модели 6.
6. Наиболее полные и совершенные нестационарные модели распространения загрязняющих веществ в атмосфере, в которые включены расчеты мезометеорологических характеристик атмосферы с учетом орографии (рельеф местности). Модели основаны на решении задач мезометеорологического прогноза и решении трехмерного уравнения переноса диффузии примеси. Требуют значительных вычислительных ресурсов и подробного задания больших объемов входной и начальной информации. Использование моделей этого класса оправдано, когда от результатов экспертизы зависят жизнь и судьбы людей, а специфика метеоусловий и орография местности таковы, что перечисленные выше модели неприменимы. Это случаи крупных аварий, имевших тяжелые последствия, или экспертиза проектов с прогнозом возможных событий, чреватых такими последствиями.
7. Модели, позволяющие прогнозировать загрязнение при штилевых условиях разных типов. Характеристики распространения и диффузии примесей в штилевых условиях и во время ветра различаются настолько, что для их описания требуются разные модели. Характер распространения загрязнения во время штиля существенно зависит от состояния атмосферы, орографии местности и начальных условий.
8. Блок моделей, позволяющих учесть процессы химической трансформации примесей. В случае необходимости его подключают к моделям 4–7. Используется в тех случаях, когда для анализа события существенным является учет химических реакций, протекающих в облаке выбросов, например, в случаях возможности значительного повышения или уменьшения токсичности. Подключение блока может значительно, в несколько раз, замедлить время работы расчетной модели.
9. Специальные модели для районирования территорий по вероятности аварий и по степени угрозы промышленным объектам и населению, которые строят на основе среднестатистических моделей с использованием информации о розе ветров данной местности. Существенным моментом при построении моделей этого класса является необходимость учета реакции объекта, подвергающегося воздействию облака выбросов. Характер реакции объекта зависит от его свойств, типа и концентрации токсичного вещества и продолжительности его воздействия. Объектом может быть и человек и промышленное предприятие. Модели для оценки загрязнения территории или объектов строятся на основе моделей 1–8. Выбор модели определяется характером необходимой оценки. Например, для оценки влияния на здоровье населения в случае выброса ядовитых газов можно использовать модель 1, в случае безвредных примесей вообще не требуется расчетов, а промежуточные случаи как всегда сложны для моделирования.
10. Комплекс синоптико-статистических моделей и автоматизированного прогнозирования неблагоприятных метеорологических условий (НМУ), предназначенный для оценки и прогнозирования уровней загрязнения атмосферного воздуха, а также принятия решения по атмосфероохранной деятельности как в краткосрочном, так и в долгосрочном аспектах. Для получения методик с высоким качеством прогнозирования необходимы исследования по диагностике погодных процессов синоптического масштаба, приводящих к реализации НМУ, и на основе этих исследований создание классификации синоптических процессов. Разработка расчетных моделей базируется на многомерном статистическом аппарате. Построение прогностических зависимостей основано на теории решения некорректных задач, что позволяет получать устойчивые решения при наличии коррелированности параметров, описывающих синоптическую ситуацию. Прогностическая система включает в себя: прием и обработку метеорологической ин- формации из каналов связи, контроль и корректировку данных, архивирование и собственно прогноз.

Перечень ссылок

1. Руководство по организации контроля состояния природной среды в районе расположения АЭС / Под ред. К.П. Махонько. Л.: Гидрометеоиздат, 1990, 264 с.
2. Techniques and decision making in the assessment of off-site consequences of an accident in a nuclear facility / Safety series, N.86, International Atomic Energy Agency. Vienne. 1987. 185 p.