УПРАВЛЕНИЕ ТРАФИКОМ В MPLS СЕТЯХ С ИСПОЛЬЗОВАНИЕМ НЕЙРОСЕТЕВЫХ МОДЕЛЕЙ

Шепеленко С.Г., Чичикало Н.И.
Донецкий национальный технический университет

Библиотека

Источник: Науковий збірник «Інтегровані інтелектуальні робототехнічні комплекси». / Матеріали ІV міжнародної науково-практичної конференції «Інтегровані інтелектуальні робототехнічні комплекси» (ІІРТК-2011).

Целью работы является разработка алгоритмов оптимизации сети с многопротокольной коммутацией по меткам (Multiprotocol Label Switching, MPLS), обеспечивающих повышение производительности за счет более эффективного распределения ресурсов пропускной способности магистральных каналов связи между набором заданных путей с коммутацией по меткам (Label Switched Path, LSP), перераспределения нагрузки между LSP в условиях изменения трафика в сети.

MPLS представляет собой технологию использования метода передачи по меткам. С помощью меток определяются и маршруты, и атрибуты услуг. На периферии сети, в точке входа, происходит обработка входящих пакетов. Здесь же выбираются и присваиваются метки. Опорная сеть считывает метки, соответствующим образом обрабатывает пакеты и передает их далее в соответствии с метками. После этого пакеты с метками передаются по опорной сети. Устройства опорной сети сервис-провайдера передают пакеты только на основе меток и не анализируют заголовки IP-пакетов. В точке выхода метки удаляются, и пакеты передаются в пункт назначения. Такой подход позволяет создавать иерархию потоков в сети MPLS и организовывать туннельные передачи

Математическая модель эффекта туннелирования в MPLS представляет собой сеть массового обслуживания с последовательными очередями (рис1).

рисунок 1

Рис. 1. Модель эффекта туннелирования в MPLS

Оцениваемыми параметрами являются среднее время обслуживания без прерывания (период занятости) и среднее время пребывания пакета в n-м узле. Обслуживаемые за период занятости пакеты объединяются в группу на выходе узла и называются пачкой. Средняя длина такой пачки выражается числом пакетов. На вход граничного узла 1 поступает пуассоновский поток сообщений с интенсивностью входного потока заявок λ и средним временем обслуживания 1/μ.

В MPLS-сети в ходе решения задач управления трафиком в рамках потоковых моделей необходимо рассчитать один или множество путей (LSP) между парой приграничных узлов отправитель-получатель, а также определить порядок распределения между ними трафика заданной интенсивности. Кроме того, с целью повышения согласованности при решении отдельных задач управления трафиком в разрабатываемой модели необходимо также описать процесс распределения канального ресурса между трафиками разных классов[2].

В MPLS существует метод восстановления услуг. Это достигается с помощью функции защиты каналов или быстрой перемаршрутизации. Это означает, что каждый канал LSP может быть защищен с помощью резервного маршрута, который начинает работать с момента отказа канала (рис2).

рисунок 2

Рис. 2. Схема MPLS сети

Прохождение пакта через MPLS сеть моделируется с помощью нейронных самообучающихся сетей. С помощью нейронных сетей решается задача маршрутизации. Маршрутизация является одной из важных задач для телекоммуникационных сетей различного назначения. Задачи, связанные с выбором маршрута, планированием работы средств связи и т. п., относятся к классу сложных комбинаторно-оптимизационных задач, как правило, не имеющих простых аналитических решений. Кроме того, сложность необходимых вычислений экспоненциально возрастает при увеличении количества узлов в сети. Поэтому в настоящее время широко применяют различные эвристические алгоритмы и процедуры, полученные путем творческого поиска, интуиции и опыта исследователя. Альтернативой существующим методам решения задач маршрутизации является использование нейросетевых моделей, которые позволяют при значительном снижении временных затрат получить хорошие субоптимальные решения. Так, для решения комбинаторно-оптимизационных задач широко используются модели построенные на основе НС Хопфилда.

Пусть заданы: граф связности сети, ряд пар NSD - исходная точка - пункт назначения (SD) и ряд линий связи, соединяющих каждую пару SD.

Теперь рассмотрим модель НС Хопфилда, используемую в этом случае для выбора маршрута между несколькими SD парами в сети. Выходные напряжения нейронов (которые и определяют их состояния) такой НС приближаются к двоичным значениям по мере перехода сети к состоянию устойчивого равновесия с минимальной "энергией". Соединения между нейронами і и j описываются весом Tij, который положителен если соединение возбуждающее и отрицателен, если соединение тормозящее (запрещающее). В рассматриваемой модели НС для каждого маршрута между каждой SD парой определяется один нейрон. Вариант модели НС для сети представлен на рис.3, нейрон ij отображает j маршрут между SD парой і.

НС эволюционирует от какого-то начального состояния до состояния равновесия, которое отображает минимум (не обязательно глобальный) функции энергии Ляпунова, которая может быть записана через веса соединений, токи смещения и напряжения на выходах нейронов следующим образом:

формула 1

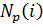В выражении Tij,kl - вес соединения между нейронами ij и кl, Ііj- ток смещения, прикладываемый к нейрону ij, формула 2 - число вариантов маршрутов, определенных между SD парой i В рассматриваемой модели веса соединений являются симметричными (т. е. Tij,kl = Tkl,ij). Эта симметрия гарантирует сходимость к устойчивому состоянию. Общее число нейронов N задастся как 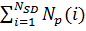формула 3. Веса соединений Tij,kl являют¬ся элементами матрицы связности размерности NxN[3].

Таким образом, целевая функция, моделируемая с помощью НС Хопфилда, включает взвешенные суммы произведений пар выходных напряжений нейрона и выходных напряжений взятых по отдельности.

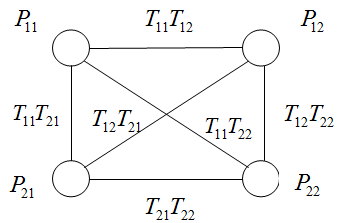
рисунок 3

Рис. 3. Модель нейронной сети

Результаты моделирования показывают эффективность рассмотренной модели для минимизации перегрузки в больших сетях.

Литература

1. А.Б. Гольдштейн – Механизм эффективного туннелирования в сети MPLS

2. Электронное научное специализированное издание –журнал «Проблемы телекоммуникаций»: http://www.nbuv.gov.ua

3. Комашинский В.И., Смирнов Д.А. – Нейронные сети и их применение в системах управления и связи, 2002;