УПРАВЛЕНИЕ ТРАФИКОМ В MPLS СЕТЯХ С ИСПОЛЬЗОВАНИЕМ НЕЙРОСЕТЕВЫХ МОДЕЛЕЙ

Шепеленко С.Г., Бессараб В.И.
Донецкий национальный технический университет

Источник: Научно-технический сборник «Автоматизация технологических объектов и процессов. Поиск молодых». / Материалы ХІ Международной научно-технической конференции «Автоматизация технологических объектов и процессов. Поиск молодых».

Целью работы является повышение производительности MPLS сети за счет более эффективного распределения ресурсов пропускной способности магистральных каналов связи между набором заданных путей, перераспределения нагрузки между LSP в условиях изменения трафика в сети.

В MPLS-сети в ходе решения задач управления трафиком в рамках потоковых моделей необходимо рассчитать один или множество путей между парой приграничных узлов отправитель-получатель, а также определить порядок распределения между ними трафика заданной интенсивности. Кроме того, с целью повышения согласованности при решении отдельных задач управления трафиком в разрабатываемой модели необходимо также описать процесс распределения канального ресурса между трафиками разных классов[1].

Основной механизм управления трафиком в MPLS – использование однонаправленных туннелей для задания пути прохождения определенного трафика.

Минимизация перегрузок является первичной задачей управления трафиком в MPLS сетях. Здесь речь идет не о кратковременных перегрузках, а о долгосрочных, влияющих на поведение сети в целом. Перегрузка обычно проявляется двояко:

1. Когда сетевых ресурсов недостаточно или они не соответствуют существующей загрузке.

2. Когда потоки трафика неэффективно распределены по имеющимся ресурсам.

Первый тип проблем перегрузки может быть решен путем расширения ресурса или применением классических средств управления перегрузкой.

Второй тип проблем перегрузки может быть решен посредством управления трафиком. Вообще, перегрузка, связанная с неэффективным размещением ресурсов, может быть уменьшена с помощью политики балансировки нагрузки в различных фрагментах сети. Задачей таких стратегий является минимизация максимальной перегрузки или напротив минимизация максимума использования ресурса. Когда перегрузка минимизирована путем оптимального размещения ресурсов, потери пакетов и задержка доставки падают, а совокупная пропускная способность возрастает. [2].

Прохождение пакта через MPLS сеть моделируется с помощью нейронных самообучающихся сетей. С помощью нейронных сетей решается задача маршрутизации. Нейросетевые модели позволяют при значительном снижении временных затрат получить хорошие субоптимальные решения. Так, для решения комбинаторно-оптимизационных задач широко используются модели построенные на основе НС Хопфилда.

Пусть заданы: граф связности сети состоящий из маршрутизаторов, ряд пар 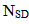, исходная точка (LSR1) пункт назначения (LSR3) и ряд линий связи, соединяющих каждую пару SD.

Теперь рассмотрим модель НС Хопфилда, используемую в этом случае для выбора маршрута между несколькими SD парами в сети. Выходные напряжения нейронов (которые и определяют их состояния) такой НС приближаются к двоичным значениям по мере перехода сети к состоянию устойчивого равновесия с минимальной "энергией". Соединения между нейронами і и j описываются весом Tij, который положителен если соединение возбуждающее и отрицателен, если соеди¬нение тормозящее (запрещающее). В рассматриваемой модели НС для каждого маршрута между каждой SD парой определяется один нейрон. Вариант модели НС для сети представлен на рис.1, нейрон ij отображает j маршрут между SD парой.

НС эволюционирует от какого-то начального состояния до состояния равновесия, которое отображает минимум (не обязательно глобальный) функции энергии Ляпунова, которая может быть записана через веса соединений, токи смещения и напряжения на выходах нейронов следующим образом:

В выражении Tij,kl - вес соединения между нейронами ij и кl, Ііj- ток смещения, прикладываемый к нейрону ij, 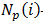-число вариантов маршрутов, определенных между SD парой i В рассматриваемой модели веса соединений являются симметричными (т. е. Tij,kl = Tkl,ij). Эта симметрия гарантирует сходимость к устойчивому состоянию. Общее число нейронов N задастся как 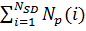. Таким образом, веса соединений Tij,kl являют¬ся элементами матрицы связности размерности NxN[3].

Таким образом, целевая функция, моделируемая с помощью НС Хопфилда, включает взвешенные суммы произведений пар выходных напря-жений нейрона и выходных напряжений взятых по отдельности.

По результатам моделирования (рис.2) сеть показывает что для определения однонаправленного туннеля TE-tunnel обходного направления быстрой перемаршрутизации прохождения трафика в сети MPLS, можно выбрать определенную последовательность LSR в направлении от LSR-1 к LSR-3.

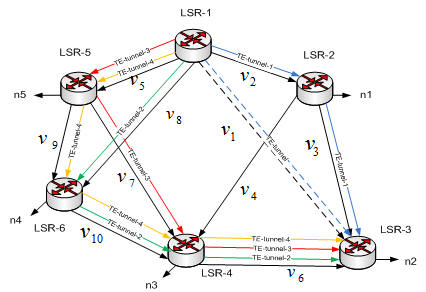
Таким образом результаты моделиро¬вания показывают эффективность рассмотренной модели для минимизации перегрузки в больших сетях. Применение нейронных моделей при решении задач маршрутизации в сети MPLS позволило обеспечить получение в аналитическом виде результатов эффективного использования сетевых ресурсов с помощью организации TE-tunnel быстрой перемаршрутизации.

Перечень ссылок

1. Электронное научное специализированное издание –журнал «Проблемы телекоммуникаций» [Электронный ресурс] - Режим доступа http://www.nbuv.gov.ua свободный. – Название с экрана

2.Требования для управления трафиком Семенов Ю.А. (ГНЦ ИТЭФ) [Электронный ресурс] - Режим доступа http://book.itep.ru/4/4/te.html свободный. – Название с экрана.

3. Комашинский В.И., Смирнов Д.А. – Нейронные сети и их применение в системах управления и связи, 2002.