НЕЙРОСЕТЕВЫЕ ТЕХНОЛОГИИ В ПРОГНОЗИРОВАНИИ ТЕЛЕКОММУНИКАЦИОННОГО ТРАФИКА

А.А. Подорожняк

Рассмотрена математическая модель телекоммуникационного трафика учитывающая его самоподобность и основанная на теории нейродинамики. Предложен метод прогнозирования телекоммуникационного трафика в реальном масштабе времени, на основе теории искусственных нейронных сетей. Предложен алгоритм синтеза нейросети для прогнозирования телекоммуникационного трафика.

Постановка проблемы и анализ литературы

В настоящее время вопросы обеспечения стойкого управления и обмена информацией между элементами сложных разнесенных систем не утратили своей актуальности. И, как хорошо известно [1 – 3], трафик телекоммуникационных систем, в том числе и трафик систем управления и обмена информацией между элементами сложных разнесенных систем, не всегда достаточно адекватно описывается традиционными моделями, не учитывающими их самоподобный характер.

Проблеме моделирования самоподобного (фрактального) трафика посвящено начительное число работ [3 – 5]. Результаты этих исследований позво-ляют определять многие характеристики трафика телекоммуникационных сетей, но у большинства моделей, предложенных в этих работах, есть один существенный недостаток – необходимо значительное время для получения и обработки информации о трафике, тогда как задачи, решаемые многими сложными разнесенными системами [4, 6] требуют проводить управление трафиком в режиме реального времени, что является актуальной научной задачей. В таком случае решить ее позволяет теория нейродинамики, в основе которой лежат методы искусственных нейронных сетей, хаоса и фракталов.

Целью данной статьи является разработка подхода к прогнозированию параметров телекоммуникационного трафика в реальном масштабе времени с учетом его фрактального характера, базирующегося на нейросетевых технологиях.

Результаты теоретических исследований

Любой процесс, в том числе и телекоммуникационный трафик, является фрактальным, если у него дробная размерность. Для изучения хаотических процессов, таких как, например поведение телекоммуникационного трафика может быть использован показатель Херста, позволяющий определить хаотичность или стохастичность анализируемого процесса. В классическом виде этот показатель может быть получен из соотношения

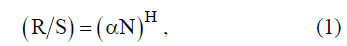
где R – максимальный размах исследуемой величины; S – ее среднеквадратичное отклонение; N – время наблюдений (или объем выборки), – некая постоянная; H – показатель Херста. Анализируя (1) можно сказать, что это форма представления различных сигналов, в том числе и параметров трафика телекоммуникационной сети на фрактальной плоскости, образованной логарифмическими координатными осями, а показатель Херста H определяет наклон аппроксимирующей прямой фрактальной линии к оси абсцисс. При этом в зависимости от значений параметра Херста, можно говорить о персистентных – сохраняющих имеющуюся тенденцию (H > 0,5) и антиперсистентных процессах (H < 0,5). В случае, когда H = 0,5, имеют место процессы, в которых тренд отсутствует. Следовательно, определяя параметр Херста телекоммуникационного трафика в процессе функционирования сети, можно провести прогнозирование требуемых параметров сети. Но классический метод Херста обладает рядом недостатков, среди которых невозможность вычисления показателя в реальном масштабе ремени ввиду значительного роста объема вычислений. Для устранения данного недостатка можно воспользоваться моделью телекоммуникационного трафика средств космической связи, предложенной в [6].

В этом случае выражение (1) может быть преобразовано в рекуррентную форму:

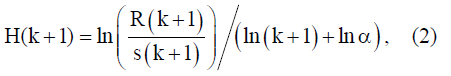
где k = 1, 2,... – соответствующие временные интервалы агрегирования трафика [5].

Проведем анализ выражения (2). Видно, что показатель Херста может уточняться на каждом шаге агрегирования без предварительного запоминания значений интенсивности трафика. Реализация предложенного алгоритма определения H может быть упрощена с помощью нейросетевых технологий. Результат вычислений параметра Херста в значительной степени зависит от параметра и объема имеющейся выборки, что может привести к тому, что для одной и той же реализации телекоммуникационного трафика могут быть получены качественно различные, а часто и противоположные результаты.

Данную проблему можно решить, воспользовавшись нейросетевыми технологиями, которые связаны с алгоритмами обучения и анализа хаотических систем [6, 7]. Тогда переписав (1) в виде

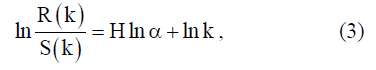
и введя обучающий сигнал для настраиваемой линейной прямонаправленной нейросеть типа адалины, для которой можно воспользоваться алгоритмом обучения Уилдроу-Хоффа [7, 8] для получения оценок неизвестных параметров:

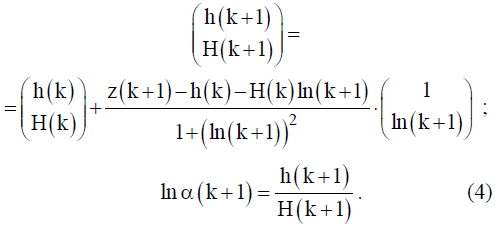
В этом случае для расчета показателя Херста и параметра сети может быть предложена соответствующая архитектура искусственной нейронной сети, которая будет функционировать параллельно контролируемого трафика, обнаруживая возникаю щие изменения в реальном времени.

Во втором варианте реализации нейросетевого подхода к прогнозированию параметров телекоммуникационного трафика в качестве основного элемента может быть использована нейросеть (рис. 1) с радиальными базисными функциями возбуждения [7].

Выходной сигнал такой сети имеет вид:

где y = [y1, ….., yK] – выход нейросети (прогнозируемые параметры трафика); k – размерность выходного вектора; – вектор, состоящий из r радиальных базисных функций нейронов скрытого слоя,с элементами

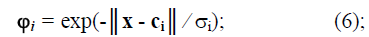
x = [x1, ….., xM] – входной сигнал нейросети (параметры текущего трафика); M – размерность входного вектора; ci = [ci1, ……, ciM] – координаты центров активационных функций, i=1,…., N; r – количество скрытых нейронов в сети; 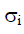– ширина активационных функций; W – выходная весовая матрица сети (размерность r*k).

Для такой сети может быть применен следующий алгоритм обучения:

1. Выберем размер скрытого слоя R равным количеству тренировочных шаблонов. Синаптические веса нейронов скрытого слоя примем равными 1.

2. Разместим центры активационных функций нейронов скрытого слоя в точках x пространства входных сигналов сети, которые входят в набортренировочных шаблонов сj = xj, j=1, 2, …, r.

3.Выберем ширину окон активационных функций нейронов скрытого слоя i, j = 1, 2,…, r достаточно большими, но так, чтобы они не накладывались друг на друга в пространстве выходных сигналов.

4.Определим веса нейронов выходного слоя сети wij, i=1, 2,…, r, j=1,2,…, k, для чего предъявим сети весь набор тренировочных шаблонов и в результате получим набор линейных уравнений, который можно записать в матричном виде:

где D – матрица (размера r*k) желаемых выходов (выходных шаблонов); Ф – интерполяционная матрица (размера r*r) элементы которой

где i = 1, 2,…, r; j = 1, 2,…, r.

Решение системы уравнений в виде 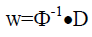обеспечивает прохождение интерполяционной поверхности через все точки тренировочного набора шаблонов.

Результаты моделирования и обработки экспериментальных данных

Было проведено моделирование в системе MATLAB [10] реального трафика телекоммуникационных сетей (рис. 2) с помощью предложенного выше подхода, использующего линейную прямонаправленную нейронную сеть, нейросеть с радиальными базисными функциями и оценки показателя Херста,проведенные с помощью классического метода.

Результаты моделирования и обработки данных приведены на рис. 3. Анализ зависимости показателя Херста для трафика от изменения длительности анализируемого участка, показывает что с увеличением анализируемого периода трафика при классическом методе точность оценки показателя Херста плавно возрастает; применение линейной прямонаправленной нейросети и РБФ-сети при изменении анализируемого периода трафика приводит к сопоставимым с классическим методом результатам.

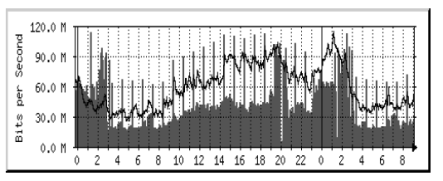
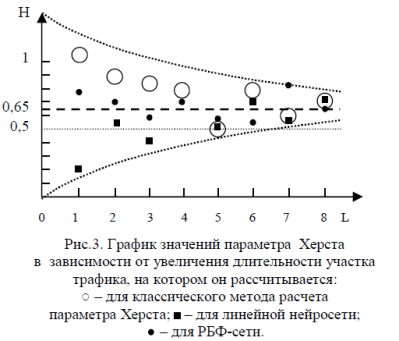
В то же время классический метод требует задания всего трафика до начала обработки, в то время как нейросеть позволяет проводить обработку трафика телекоммуникационной сети одновременно с его функционированием.

Выводы

В результате теоретических исследований моделирования телекоммуникационного трафика системы космической связи с помощью теории нейродинамики, используя аппарат линейных прямонаправленных нейросетей, предложен усовершенствованный метод определения показателя Херста, который позволяет проводить исследования телекоммуникационного трафика в реальном масштабе времени. Сопоставление предложенного метода с известными в настоящее время [2 – 5] подтвердило достоверность результатов, полученных новым методом, несомненным достоинством которого являются меньшие временные затраты на его реализацию.

Список литературы

1.Столлингс В. Современные компьютерные сети. –С-Пб.: Питер, 2003. – 784 с

2.Кучук Г.А., Можаев О.О., Воробйов О.В. Аналіз та моделі самоподібного трафіка // Авиационно-космическая техника и технология. – 2006. – № 9 (35). – С. 173-180.

3.Leland W., Taqqu M., Willinger W. On the selfsimilar nature of IP-trafic // IEEE/ACM Transactions on Networking. – 1997. – № 3. – P. 423-431.

4.Кучук Г.А., Можаeв А.А., Руккас К.М. Фрактальный анализ процессов, структур и сигналов // Коллективная монография под ред. Р.Е. Пащенко – Х.: ЭкоПерспектива, 2006. – 360 с.

5.Кучук Г.А., Можаєв О.О., Воробйов О.В. Метод агрегування фрактального трафіка // Радіоелектронні та комп’ютерні системи. – 2006. – № 6 (18). – С. 181-188.

6. Можаев А.А., Подорожняк А.А., Воробьев О.В. Нейродинамическое прогнозирование телекоммуникационного трафика средств космической связи // Авиационно-космическая техника и технология. – 2006. – № 6 (32). – С. 67-70.

7.Руденко О.Г., Бодянский Е.В. Основы теории искусственных нейронных сетей. – Х.: ТЕЛЕТЕХ, 2002. – 317 с.

8.Медведев В.С., Потемкин В.Г. Нейронные сети.MATLAB 6. – М.: Диалог – МИФИ, 2002. – 416 с.