Введение

При передаче цифровой информации особое внимание уделяется вопросам синхронизации. В частности при использовании PSK сигналов требуется производить различение передаваемых символов по фазе. Но опорные генераторы на передающей и приемной стороне не могут быть когерентны, поэтому прибегают с следящим контурам (петлям), позволяющим производить подстройку генераторов опорных сигналов для когерентной демодуляции. Такие следящие системы называют контурами фазовой автоподстройки частоты ФАПЧ (phase-locked loop PLL). О них пойдет речь в данной статье. Разумеется в одной статье невозможно изложить все что касается теории следящих систем, поэтому за более подробной информацией рекомендую обратиться к работам [G2] и [N1].

Структурная схема контура фазовой автоподстройки частоты

Структурная схема контура фазовой автоподстройки частоты (ФАПЧ) показана на рисунке 1.

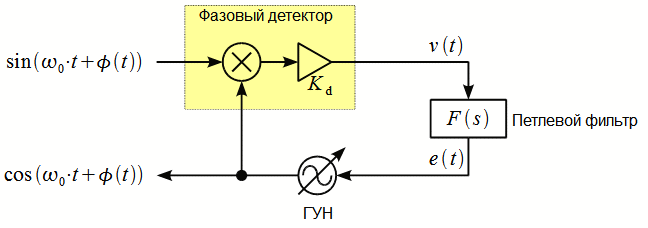
В состав контура входит фазовый детектор, представляющий собой умножитель с коэффициентом усиления K_d, петлевой фильтр F(s) (в англоязычной литературе loop filter), который формирует управляющее напряжение (или сигнал ошибки) e(t) и генератор управляемый напряжением (ГУН). Прежде чем переходить к рассмотрению принципов функционирования контура поясним как работает ГУН.

Генератор управляемый напряжением (ГУН) и его свойства

Следящий контур фазовой автоподстройки частоты должен постоянно вести сопровождение входного сигнала по фазе. Соответственно, генератор, входящий в состав контура должен «уметь» перестраиваться по фазе. Для этого разработаны генераторы управляемые напряжением (ГУН), или в англоязычной литературе voltage-controlled oscillator (VCO), мгновенная частота сигнала на выходе которых зависит от управляющего напряжения как это показано на рисунке 2.

На входе генератора управляющее напряжение (сигнал ошибки) e(t), а на выходе сигнал, полная фаза Φ(t) которого равна (все что под косинусом)

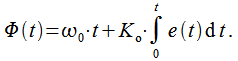
Тогда мгновенная частота на выходе генератора ω(t)=dΦ/dt=ω₀+K₀e(t) представляет собой производную от полной фазы и пропорциональна текущему управляющему напряжению e(t), K₀ – коэффициент пропорциональности. На рисунке показан пример зависимости мгновенной частоты на выходе ГУН от управляющего напряжения e(t).

Анализ структурной схемы контура ФАПЧ

Рассмотрим теперь структурную схему показанную на рисунке 1. Для упрощения введем следующее обозначение:

тогда сигнал на выходе ГУН равен cos(ω₀t+ψ(t)), а сигнал на выходе фазового детектора:

Сигнал на выходе фазового детектора представляет собой сумму сигнала на удвоенной частоте 2ω₀ и сигнала зависящего от разности фаз входного сигнала и ГУН. Петлевой фильтр представляет собой ФНЧ, который подавляет сигнал на удвоенной частоте, тогда на выходе петлевого фильтра получим управляющий сигнал e(t):

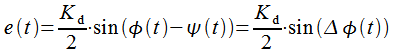
Управляющий сигнал на выходе петлевого фильтра пропорционален синусу разности фаз принятого и опорного сигналов.

Статические и астатические ошибки при работе контура ФАПЧ. Порядок астатизма

В литературе по радиоавтоматике ошибки принято разделять на статические и астатические. Что такое статическая и астатическая ошибка? Ошибка называется статической, если в режиме слежения сигнал ошибки постоянный e(t)=const и отличен от нуля, и называется астатической если e(t)=0. Поясним это на примере.

Пусть петлевой фильтр отсутствует, тогда сигнал на выходе фазового детектора v(t) есть сигнал ошибки v(t)=e(t) . В установившемся режиме сопровождения полные фазы принятого сигнала и сигнала на выходе ГУН полностью совпадают, тогда можно записать:

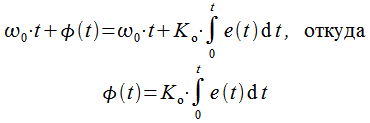
Пусть фаза φ(t)=φ₀=const, т. е. принятый и опорный сигналы различны по фазе, но их частоты совпадают, тогда уравнение (5) принимает вид:

Продифференцировав обе части выражения (6) относительно времени можно выразить сигнал ошибки в установившемся режиме:

Если ГУН управляется непосредственно сигналом с фазового детектора, то при рассогласовании по фазе входного сигнала и опорного сигнала мы получим астатическую ошибку. Теперь рассмотрим как поведет себя эта система, если сигналы отличны не только по фазе но и по частоте, т. е. φ(t)=Δωt+φ₀, где Δω – частотное рассогласование. Уравнение (5) в этом случае принимает вид:

продифференцировав которое мы получим

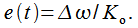
Таким образом при частотном рассогласовании мы получим статическую ошибку. И это понятно, фазовый детектор показывает текущее фазовое рассогласование, при этом ГУН его компенсирует, но в следующий момент времени оно снова возникает из-за частотного набега фазы и снова фазовый детектор его фиксирует. В этом случае ГУН постоянно «накручивает» свою фазу, пытаясь скомпенсировать тот фазовый набег, который возник в результате частотного рассогласования. При статической ошибке контур все еще в состоянии вести слежение за сигналом.

Продолжая рассмотрение данного примера можно ввести квадратичный член в φ(t), который будет характеризовать изменение частоты во времени. В этом случае ошибка будет линейно зависеть от времени и контур не сможет отслеживать такой сигнал.

В приведенном примере астатическая ошибка была только в случае постоянного рассогласования. В этом случае говорят об астатизме первого порядка. Если контур ФАПЧ обеспечивает астатическую ошибку e(t)=0 при фазовом и частотном рассогласовании, то говорят, что контур имеет второй порядок астатизма. В этом случае контур ФАПЧ отслеживает сигнал и при изменении его частоты во времени, т. е. при квадратичном члене в φ(t).

На практике контур ФАПЧ должен отслеживать не только постоянное фазовое рассогласование, но и частотное рассогласование, которое может медленно меняться во времени. Таким образом нам необходим контур с порядком астатизма равный двум.

Сделаем замечания.

Замечание 1. Порядок астатизма контура ФАПЧ полностью определяется порядком передаточной характеристики контура (речь об этом пойдет ниже). Для обеспечении контура второго порядка астатизма необходимо, чтобы петлевой фильтр был первого порядка.

Замечание 2. У читателя может сложится впечатление, что увеличивая порядок астатизма можно легко получить следящие системы, которые будут отслеживать высокодинамичные изменения. На практике это не совсем так. Дело в том, что наш контур – контур с обратной связью, который должен быть проверен на устойчивость. При этом гарантировать устойчивость контура с порядком астатизма выше второго аналитически возможно только в частных случаях. Поэтому контуры с порядком астатизма выше второго используются только в исключительных случаях, а их построение - нетривиальная задача.