Microwave and Wireless Synthesizers. / Ulrich L. Rohde, 1997.
1-3 DIGITAL LOOPS
Using our previous definition, a digital PLL is a PLL system in which the phase/frequency comparator is built from digital components such as gates or flip-flops to form either an exclusive-OR gate, an edge-triggered JK master/slave flip-flop, or what I call a tri-state phase/frequency comparator. In addition, digital PLLs use frequency dividers, and although some circuits using the principle of subharmonic locking for dividers are known, this generally refers to the use of asynchronous or synchronous dividers. Asynchronous dividers are usually ripple counters, and synchronous dividers are counters that are being clocked by a common reset line.
The basic difference between an analog and a digital phase/frequency loop is in the possible delay introduced by the frequency divider and the nonlinear effects of the phase/frequency comparator, and the question of ultimate resolution of the phase/frequency comparator. The phase/frequency comparator using active filters shows some highly nonlinear performance during zero crossings at the output or under perfectly locked conditions. As there is no output from a tri-state phase/frequency comparator under locked conditions, the gain of the loop is zero until there is a requirement to send correcting pulses from the digital phase/frequency comparator, which then results in a jump of loop gain.
We will prove that digital phase/frequency comparators, especially tri-state phase/frequency comparators, have two ranges for acquisition. One is called pull-in range, and the other is called lock-in range. The acquisition time is the time for both. This total time to acquire both frequency and phase lock is sometimes called capture time or digital acquisition time. Depending on the loop filter and the phase/frequency comparator, we will have different time constants.
For reasons of convenience and linearity, we have, so far, assumed that the loop is in locked condition. Initially, when the loop is switched on for the first time, it is far from being locked, and the VCO frequency can be anywhere within tuning range. Tuning range is defined as the frequency range over which the voltage-controlled oscillator (VCO) can be tuned with the available control voltage.
There are, however, limitations because of the tuning diodes. The minimum voltage that can be applied is determined by the threshold voltage of the diode itself before it becomes conductive. This voltage is typically 0.7 V, and the maximum voltage is the voltage determined by the breakdown voltage of the tuning diode. Even in the case where the familiar back-to-back diode arrangement is used, these are the two limits for the voltage range. In practice, however, this range is even more narrow because the voltage sensitivity of the tuning diode is excessive at the very low end and very small at the extreme high end. Even before the breakdown voltage is reached, the noise contribution from the diode already increases because of some zener effects.
As the loop currently is not in locked condition, we have to help it to acquire lock. Very few loops acquire locking by themselves, a process called self-acquisition. Generally, the tuning range is larger than the acquisition range. Self-acquisition is a slow, unreliable process. If the loop is closed for the first time, the process called "pull-in" will occur. The oscillator frequency, together with the reference frequency, will generate a beat note and a dc control voltage of such phases that the VCO is pulled in a direction of frequency lock. As the oscillatoritself generates noise in the form of a residual FM, the oscillator is constantly trying to break out of lock, and the loop is constantly monitoring the state and reassuring lock. This results, under normal circumstances, in constant charging and discharg¬ing of the holding capacitor responsible for the averaging process.
There is one other phase/frequency comparator that is really more a switch than anything else; it is called a sample/hold comparator. The sample/hold comparator, which we will deal with later, has the advantage of very good reference frequency suppression, introduces a phase shift that reduces the phase margin, and is really useful only up to several hundred kilohertz of frequency. For frequencies higher than this, there is too much leakage. The sample/hold comparator, which has been very popular for several years, is described in Chapter 4. Modern frequency synthesizers, however, prefer digital phase/frequency comparators because the sample/hold comparator is only a phase comparator and does not recognize frequency offsets. It is too slow to be used for harmonic sampling and, in my opinion, has only limited use.
The sample/hold comparator is used mostly with T networks for additional reference suppression, and although these circuits provide good reference suppression, the phase margin has to be so high that the loops are generally slow in their response.
The switching speed of the loop and its general performance to noise are covered in detail in Section 1-10.
Now let us take a look at a numerical example. Consider a frequency synthesizer using a PLL to synthesize a 1 MHz signal from a 25-kHz reference frequency. To realize an output frequency of 1 MHz, a division of 1 MHz/25 kHz = 40 is necessary.
Let us assume that there is no filtering included, and therefore the closed-loop transfer function will be
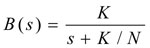
A typical value for Kθ is 2 V/rad and a typical value for the VCO gain factor K0 is 1000 Hz/V. With these values the closed-loop transfer function is
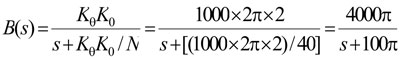
The 3-dB frequency of the system by definition is
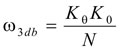
and therefore
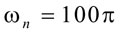
is solved to determine f, we obtain f = 50 Hz.
As the reference frequency is 25 kHz, the reference suppression of the simple system can be determined from
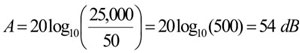
The loop bandwidth of the system by itself is 50 Hz.
We have, with very little effort, calculated a first-order type 1 loop. We deal more with these loops in Chapter 2.
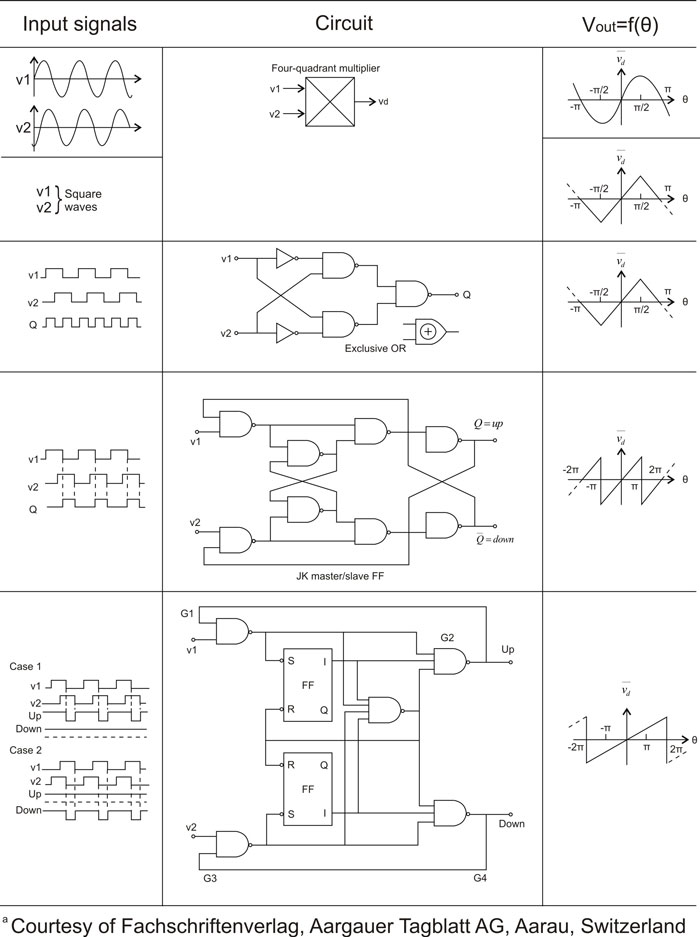
Table 1-2 shows the input waveforms and the output average voltage of:
- A four-quadrant multiplier or double-balanced mixer being driven either by a sine wave or a square wave.
- The input and output voltages for an exclusive-OR gate.
- The input and output voltages after the integrator of an edge-triggered JK master/slave flip-flop.
- The input and output voltages of a tri-state phase/frequency comparator after the integrator. Notice that the extended operating range is linear from — 2π to +2π.
Table 1-2 Circuit diagrams and input and output waveforms of various phase/frequency comparatorsa