ИССЛЕДОВАНИЕ ХАРАКТЕРИСТИК ФРАКТАЛЬНЫХ ПРОЦЕССОВ ПОТОКОВ ДАННЫХ МУЛЬТИСЕРВИСНЫХ СЕТЕЙ
Жалейко Е.В., Воропаева В.Я.
Abstract: There is analyzed the different types of traffic, investigated the main characteristics of fractal processes of the individual data streams, considered the combined flow and revealed dependence of the level of self-similarity of the number of multiplexed streams.
Общая постановка проблемы. С точки зрения современных тенденций развития телекоммуникаций актуальной задачей является построение конвергентной мультисервисной сети. Такая сеть должна обеспечивать неограниченный набор услуг, предоставлять гибкие возможности по управлению и созданию новых видов сервиса. Последнее требует реализации универсальной транспортной сети с распределенной коммутацией, где взаимодействие между устройствами и приложениями осуществляется с помощью создания виртуальных соединений, на управление которыми заметно влияют особенности стохастической динамики процессов пакетной коммутации [1].
Одной из наиболее актуальных проблем исследования вероятностно-временных характеристик сетей является адекватный учет особенностей сетевого трафика. Классические подходы теории телетрафика базируются на предположении, что входящие потоки являются стационарными пуассоновскими, т.е. представляют собой суперпозицию большого числа независимых стационарных ординарных потоков без последействия равномерно малой интенсивности [2]. Для телефонных сетей с канальной коммутацией такое предположение справедливо. Но анализ результатов исследований и экспериментов по измерению характеристик трафика информационных сетей с пакетной коммутацией [3–6] демонстрирует наличие корреляции длин интервалов времени как для моментов поступления запросов в систему, так и для моментов окончания обслуживания, что является признаком наличия последействия. В современных мультисервисных сетях такая тенденция еще более усиливается.
Этой проблемой занимались многие специалисты. Начиная с публикации Леланда и др. «О самоподобной природе трафика Ethernet», зарубежные и отечественные ученые рассматривали фрактальные модели сетевого трафика в применении к протоколам разного уровня проводных и беспроводных пакетных сетей. Среди российских и украинских исследователей необходимо отметить работы О.И.Шелухина, Б.С. Цыбакова, А.В. Осина, А.Г. Ложковского, А.В. Рослякова, В.В. Петрова, Г.А. Кучука. Так, например, в работе [3] авторы показали, что в сетях стандарта 802.16 b самоподобные свойства трафика проявляются как на канальном, так и на транспортном уровнях. Получены значения основных показателей степени фрактальности сетевого трафика и предложены методы агрегирования исходной статистики [5]. Однако нет общепризнанных выводов о значениях характеристик фрактальных процессов для разных видов служб мультисервисных сетей и для объединенного потока.
Постановка задач исследования. Определение характеристик фрактальных процессов различных потоков данных в мультисервисных сетях крайне важно для последующего принятия решения о способе управления ими. Для решения поставленной задачи необходимо:
– исследовать трафик данных, аудио-, видеотрафик;
– проанализировать объединенный поток;
– сделать вывод о зависимости уровня фрактальности суммарного потока от самоподобных свойств потоков, которые он в себе содержит.
Решение задач и результаты исследований.. Сети с коммутацией пакетов используют модели систем с ожиданием для описания сетевых устройств. При этом основные расчеты выполнены для классической модели М/М/v/W [1]. Эта модель имеет ряд предположений и упрощений: во-первых, длина очереди не ограничивается, что конечно не выполняется для любого сетевого оборудования. Во-вторых, время обслуживания пакетов устройствами коммутации или маршрутизации в этой модели считается экспоненциально-распределенным. Как показано в [5], при широком спектре действующих в сети протоколов следует принимать произвольный закон распределения времени обслуживания, т.е. использовать модель М/G/v/W.
В-третьих, входящий поток считается простейшим со свойствами стационарности, ординарности и отсутствия последействия. Указанные свойства обеспечиваются, если поток формируется бесконечным количеством источников, причем в каждый момент времени активируется не более одного источника, а интервал между двумя соседними пакетами потока случайная величина с экспоненциальным распределением. Такой подход справедлив для голосового трафика, может с определенными допущениями быть принят для трафика данных, который характеризовался определенным уровнем пачечности, но не требовал минимальных задержек. Эти предположения позволяли использовать марковские случайные процессы для моделирования таких систем.
Но исследования мультимедийного трафика, пачечность которого значительно выше на фоне требований к обслуживанию в режиме реального времени, свидетельствуют о его самоподобной природе, которая существенно ухудшает показатели качества обслуживания по сравнению с пуассоновскими потоками. На качественном уровне самоподобие проявляется в наличии медленно убывающей зависимости между параметрами трафика (в частности, дисперсии длины кадров или коэффициента автокорреляции) в разные моменты времени. Мультимедийный трафик имеет высокий уровень пачечности, причем эти пачки данных статистически подобны в широком диапазоне изменения масштаба времени.
Как известно [5], процесс называется самоподобным с параметром H=1-(b/2), если его коэффициент автокорреляции
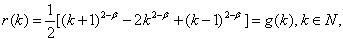
где функция g(k) выражена через центральный разностный оператор 2-го порядка
Самоподобие проявляется в том, что для процесса , который удовлетворяет условию (1), выполняется равенство rm(k)=r(k), то есть в таком процессе не изменяется коэффициент автокорреляции после усреднения по блокам какой-либо длинны m. Таким образом, для самоподобного процесса статистические характеристики второго порядка нормированного агрегированного процесса X(m) не отличается от характеристик выходного процесса X при значительном интервале изменений m.
Параметр H является индикатором степени самоподобия процесса, а также свидетельствует о наличии у него таких свойств как персистентность/антиперсистентность и длительная память. Для марковских процессов (без последействия) коэффициент Херста равняется 0,5. Процесс является полностью случайным, соответственно, простейший (Пуассоновский) поток еще называют «потоком чистой случайности первого рода.
При HЄ[0, 0.5] процессу свойственна антиперсистентность: высокие значения процесса идут за низкими и наоборот. То есть, вероятность того, что на k+1 шаге процесс отклонится от среднего в противоположном направлении (относительно отклонения на k шаге), настолько велика, насколько параметр H близок к 0.
В случае HЄ[0.5, 1] процесс является персистентным или с длительной памятью: если в течение какого-то времени в прошлом наблюдалось увеличение параметров процесса, то и в будущем в среднем будет происходить их рост. Иными словами, вероятность того, что на шаге k+1 процесс отклонится от среднего в том же направлении, что и на k шаге, настолько велика, насколько параметр H близок к 1.
Для того чтобы подтвердить существование свойства самоподобия для разных потоков данных мультисервисной сети, необходимо произвести измерения некоторых характеристик разных видов сетевого трафика. Для этого нам необходимы статистические данные о таких потоках, как аудио, видео и трафик данных, а также нужно провести исследования объединенного потока.
В качестве исходных данных возьмем время между поступлениями пакетов при различных видах трафика. Эти данные были получены с помощью программы Wireshark путем ее настройки соответствующим образом:
– для наблюдения потока данных осуществлялся просмотр Web-страниц в сети Internet;
– для наблюдения видео трафика просматривалось видео в он-лайн режиме;
– для наблюдения аудио трафика прослушивалась музыка в режиме он-лайн.
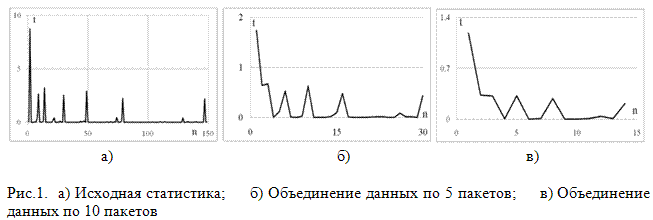
Исследуем трафик данных – обращений пользователей к Web-серверу. Полученный временной ряд содержит 150 наблюдений, каждое из которых является интервалом времени между поступлениями пакетов. После снятия характеристик трафика потока данных строим зависимость между временем поступления пакета и его номером (рис. 1а). Затем производим агрегирование данных по 5 (рис. 1б) и 10 (рис. 1в) пакетов. При изменении шкалы построения трафика, мы можем наблюдать самоподобие. Этот факт является предпосылкой для проведения дальнейшего анализа.
Чтоб оценить тяжесть хвоста для имеющихся данных, строим в логарифмическом масштабе график дополнительного распределения. График приведен на рисунке 2.
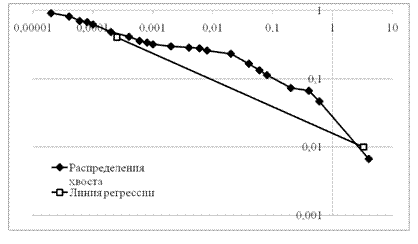
Рис. 2 – Функция распределения хвоста
Для того чтоб найти значение коэффициента a, который характеризует тяжесть хвоста распределения, необходимо построить функцию регрессии. Для этого воспользуемся стандартной функцией программы Excel «Линейн», которая позволяет построить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные.
Значение a рассчитываем, исходя из следующего равенства
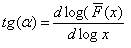
Значение параметра самоподобия H рассчитываем по формуле H=(3-a)/2. В результате расчетов получаем значение H=0,7595.
Как видим, значение Н попадает в промежуток от 0,5 до 1, что подтверждает предполагаемое свойство самоподобия рассматриваемого процесса.
Аналогично снимаем характеристики аудио- и видеотрафика, следим за сохранением их структуры при изменении масштаба и рассчитываем показатель Херста. Таким образом, получаем Н=0,7158 и Н=0,7152 соответственно для каждого вида трафика.
Для того чтоб сделать выводы о том, насколько самоподобие различных видов трафика влияет на поведение общего потока в сети, необходимо провести аналогичные наблюдения и расчеты объединенного потока. На рисунке 3 приведены зависимости между временем поступления пакетов и их номерами для суммарного трафика.
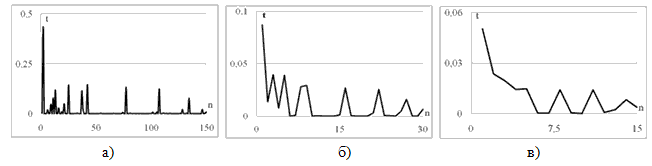
Рис.3. а) Исходная статистика; б) Объединение данных по 5 пакетов; в) Объединение данных по 10 пакетов
Далее с помощью построения функции распределения хвоста, определяем параметр Херста, который установился на уровне 0,7625. Подобные результаты получены и в других работах [4], подтверждая вывод: чем больше мультиплексируемых потоков объединяется в канале передачи, тем выше показатель Херста для объединенного потока.
Таким образом, статистическое мультиплексирование без учета характеристик фрактальных процессов, которое лежит в основе передачи информации почти во всех телекоммуникационных сетях, является малоэффективным. Этот факт позволяет вести дальнейшие исследования в направлении поиска путей оптимального управления самоподобным трафиком в сетях с пакетной коммутацией.
Выводы
1. Определены характеристики фрактальных процессов различных видов трафика мультисервисных сетей. Коэффициент Херста для потока данных равен 0,7595, для аудиотрафика этот показатель составляет 0,7158 и для видеотрафика Н=0,7152.
2. По результатам исследования можно сделать вывод, что при объединении различных типов трафика, показатель Херста устанавливается выше, чем у отдельно взятых потоков, поскольку он составляет 0,7625.
3. Повышающийся уровень самоподобия при объединении различных потоков данных в мультисервисных сетях необходимо учитывать при разработке алгоритмов управления ними.
Литература.
1. Воропаєва В.Я. Оцінка показників якості NGN-мереж з урахуванням фрактальності вхідного трафіку. // Наукові праці Донецького національного технічного університету. Серія: Обчислювальна техніка та автоматизація. Випуск 15 (130). – Донецьк-2008. – 214 с. С. 23-29.
2. Крылов В.В., Самохвалова С.С. Теория телетрафика и ее приложения. – СПб.:БХВ-Петербург, 2005. – 288с.
3. Платов В.В., Петров В.В. Исследование самоподобной структуры телетрафика беспроводной сети //Электротехнические и информационные комплексы и системы. – 2004. – №3. – с.38-49.
4. Шелухин И.О., Матвеев С.Б., Пастухов А.С. Оценка самоподобия трафика в сети широкополосного доступа WiMAX // Электротехнические и информационные комплексы и системы. – 2008. – №1. – с.88-96.
5. Бельков Д.В. Исследование сетевого трафика // Наукові праці Донецького національного технічного університету. Серія: Інформатика, кібернетика та обчислювальна техніка. Випуск 10 (153). – Донецьк-2009. – 368 с. С.212-215.