МАТЕМАТИЧЕСКАЯ МОДЕЛЬ САМОПОДОБНОГО ТРАФИКА

О.В. Воробьев, А.А. Подорожняк.

Источник: http://www.nbuv.gov.ua/portal/natural/Sunz/2007_1/Vorobev.pdf

Введение.Как показывает опыт локальных войн на Ближнем Востоке и в Восточной Европе, современная тактика ведения боевых действий характеризуется значительным увеличением объемов используемой информации как на этапе подготовки, так и в ходе боевых действий.

В США и НАТО уже фактически созданы и функционируют автоматизированные системы подготовки и нанесения массированных ударов разнородными силами и средствами, в том числе и высокоточным оружием для решения различных задач (центры планирования воздушных операций).

В состав таких систем входят средства разведки космического, воздушного, наземного и морского базирования, средства связи и навигации, пункты управления, средства нападения и поражения, развернутые на земле и в воздушно-космическом пространстве и объединенные для решения задач разведки требуемых объектов, организации и нанесения по ним массированных ракетно-авиационных ударов (МРАУ).

Системы позволяют, фактически в реальном масштабе времени, получать всю необходимую информацию о группировках войск, возможных объектах удара и обстановке в районе боевых действий, хранить ее в базе данных, систематически уточнять и использовать для принятия решения и планирования как наступательных, так и оборонительных операций [1].

Вполне очевидно, что все это ведет к значительному росту нагрузок в системах передачи данных (СПД) автоматизированных систем управления войсками (АСУВ).

Учитывая эти особенности, разработку новых автоматизированных средств боевого управления естественно создавать на основе современных информационных технологий. Современное программное обеспечение в комплексе с сетевыми и телекоммуникационными технологиями позволяет эффективно решать многие задачи, которые возникают при автоматизации процессов управления силами и средствами Вооруженных Сил Украины [2, 3].

Современная распределенная телекоммуника- ционная сеть (ТКС) – это объект высокой структурной сложности, теория построения которой находится на стадии становления.

Традиционно теория телетрафика базировалась на классической теории массового обслуживания и информации, что позволяло достаточно полно описывать процессы, протекающие в системах передачи информации, построенных на технологии коммутации каналов. С появлением сетей с пакетной передачей данных, которые стали все больше вытеснять сети с коммутацией каналов, экспериментально установлено, что трафик современных сетей имеет иную, фрактальную структуру, отличную от принятой в классической теории. Особенностью такой структуры трафика является: наличие последействия и масштабная инвариантность статистических характеристик [4 – 6].

Постановка задачи и анализ литературы. Работы [8 – 12], описывающие свойства самоподобного телекоммуникационного трафика, показали, что к настоящему времени отсутствуют как общепризнанные модели трафика, которому присущи свойства самоподобия, так и анализ причин проявления этих свойств.

Как выяснилось, для такого трафика методы расчета, которые традиционно базируются на пуассоновских моделях и формулах Эрланга, дают неоправданно оптимистические решения и приводят к недооценке реальной нагрузки.

Для повышения эффективности функционирования ТКС необходимо решить актуальную задачу прогнозирования телетрафика с учетом его самоподобного характера.

Целью данной статьи является анализ причин возникновения самоподобного трафика и моделирование этого процесса.

Основная часть.Моделирование самоподобного трафика на основе ансамбля квазипериодических источников. Перечислим некоторые из основных факторов, которые могут вызывать в сетевом трафике фрактальные случайные процессы: поведение пользователя; генерация структуры и поиск данных; объединение трафика; средства управления сетью; механизмы управления, основанные на обратной связи; развитие сети.

Рассмотрим генерацию телекоммуникационного трафика как совокупность независимых парциальных источников. Проведем моделирование парциального источника сети, как источника периодического или квазипериодического сигнала со значениями амплитуды A(t) и частоты w , эквивалентными статистическим параметрам трафика парциальных источников при постоянной нагрузке.

Математическую модель, описывающую синтез трафика в результате слияния множества парциальных источников, с учетом работы протокола ТСР по управлению нагрузкой, можно представить в виде разложения в ряд Фурье, квазипериодической, формируемой многими парциальными источниками нагрузки.

.

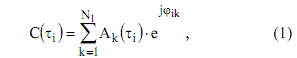Однако говорить о предложенной модели, как о модели трафика, обладающего свойствами самоподобия, в полной мере нельзя, хотя экспериментально [7] показано, что данная модель может характеризоваться масштабной инвариантностью статистических характеристик и медленно убывающей зависимостью (МУЗ) автокорреляционной функции [8, 9].

Случайная величина Z , характеризующаяся МУЗ, чаще всего обладает распределением с так называемым «тяжелым» хвостом, которое можно представить аналитически как

Описанная модель удобна для анализа причин возникновения самоподобия трафика за счет работы механизмов управления.

Моделирование самоподобного трафика на основе ON/OFF источников. ON/OFF-модель используется для объяснения физических причин самоподобных явлений в современных телекоммуникационных сетях. Самоподобные характеристики, как предполагается, в большей мере вытекают из плотности распределения с тяжелым хвостом последовательности ON/OFF-состояний. Традиционная ON/OFF-модель генерирует процесс, который является почти гауссовским процессом, полученным от 2400 пар ON/OFF-источников.

Учитывая, что нагрузка разделяется на периоды передачи сообщений (ON-периоды) и паузы (OFF-периоды), а передача сообщений характеризуется периодами активности (ON) и молчания (OFF), обозначим через ? ? i 1 G ? дискретную величину, характеризующую активность источников во время обработки транзакций в каждый период активности и запишем ее как

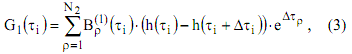
а через G(t)– дискретную величину, характеризующую процесс передачи пакетов (сегментов) в периоды активности источников и запишем ее как

Тогда процесс формализованного амплитудного состояния ON/OFF-источников G(t) , характеризующий суммарную нагрузку, можно записать в виде

.

Проанализировав выражения (2) – (5), учитывая, что в (3) и (4) описаны независимые процессы и что эти процессы подобны, но не идентичны, можно сделать вывод о том, что произведение в выражении (5) можно интерпретировать как показатель степени, близкий по значению к 2, а следовательно, и само выражение (5) является распределением с тяжелым хвостом.

Моделирование самоподобного трафика синтезом ансамбля квазипериодических источников и формализованных ON/OFF-состояний. Приведенное выше выражение (5) характеризует лишь формальные амплитудные состояния, обусловленные количеством парциальных источников. Для того, чтобы предложенная модель более адекватно отображала свойства самоподобного трафика, необходимо также учесть и суммарную нагрузку от множества парциальных источников.

Поскольку C1(ti)– разложенная в ряд Фурье, квазипериодическая, формируемая многими парциальными источниками нагрузка, а G(ti) – процесс формализованного амплитудного состояния ON/OFF-источников, характеризующий суммарную нагрузку, то очевидно, что интенсивность информационного потока l(ti) , вырабатываемого рассматриваемыми парциальными источниками, можно записать в виде

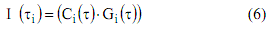
или, подставив (1) в (6), получим:

что по сути и является целевой функцией предлагаемой математической модели самоподобного трафика, полученного синтезом ансамбля квазипериодических источников и формализованных ON/OFF-состояний.

В заключение следует добавить, что на основе предложенной модели была разработана схема имитационного моделирования в системе MATLAB и проведен статистический анализ полученных процессов. Результаты анализа одной из реализаций представлены на рисунках ниже. На рис. 1 представлены исходный (а) и агрегирован- ные с шагом агрегирования m ((б) m=75, (в) m=100) синтезированные модели трафика. Даже визуально можно проследить на рисунках присущее самоподобным процессам свойство масштабной инвариантности.

На рис. 2 представлены графики автокорреляционных функций рассматриваемых процессов. Как видно, и для автокорреляционной функции этого процесса свойственна МУЗ и масштабная инвариантность при различных шагах агрегирования.

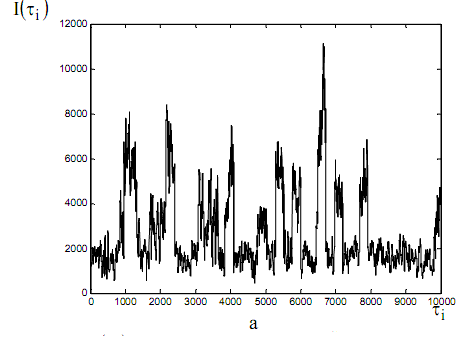
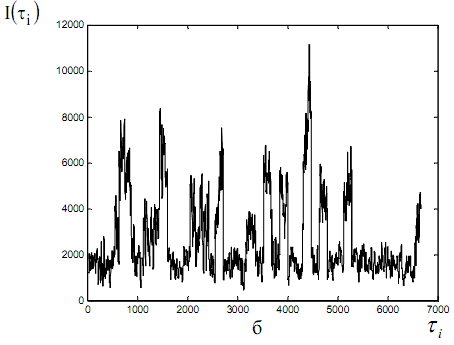
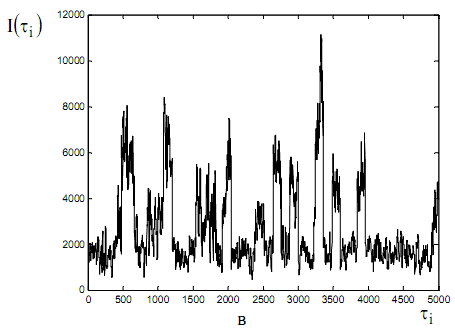
Рис. 1. - Прооцессы: а – исходный синтезированный; б – агрегированный с шагом m = 75; в – агрегированный с шагом m=100"

На рис. 3 представлены гистограммы исходной и агрегированных реализаций синтезированного процесса. Учитывая характер зависимости и свойство масштабной инвариантности, также можно сделать вывод об адекватности плотности распределения нагрузки представленной модели плотности распределения нагрузки в реальном телекоммуникационном трафике.

Рис. 2 - Графики автокорелляционных функций: а – исходный синтезированный процесс; б – процесс, агрегированный с шагом m = 75; в – процесс, агрегированный с шагом m = 100

На рис. 4 представлены результаты анализа статистических характеристик реального Internet-трафика. Сравнительный анализ статистических характеристик модели трафика и реального Internet-трафика указывает на то, что и плотность распределения нагрузки, и характер автокорелляционной функции, и очевидное свойство масштабной инвариантности синтезированного процесса адекватны характеристикам телекоммуникационного трафика.

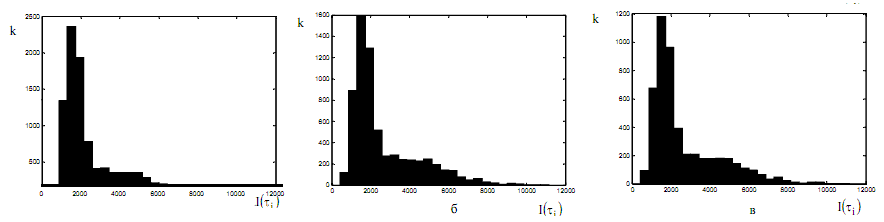Рис. 3. Гистограммы: а – исходного синтезированного процесса; б – процесса, агрегированного с шагом m = 75; в – процесса, агрегированного с шагом m = 100

Подробнее процесс и анализ имитационного моделирования описан в работе [7]. Одним из более значимых в определении принадлежности процесса к самоподобным является показатель Херста Н. Известно, что его значение должно лежать в пределах от 0 до 1 [7]. В данном случае его значение Н = 0,75 – для предложенной модели и Н = 0,8 – для реального Internet-трафика, что также является подтверждением адекватности предложенной модели телекоммуникационному трафику с фрактальными свойствами.

Выводы.В статье предложена математическая модель процесса слияния независимых пульсирующих информационных потоков и сделано предположение, что результирующий процесс имеет самоподобные свойства с более выраженной автокорелляционной зависимостью, но с менее выраженной плотностью распределения с точки зрения весомости хвоста.

Получила дальнейшее развитие математическая ON/OFF-модель, которая имеет подобные свойства, но с четко выраженной тяжестью хвоста плотности распределения.

Наиболее полной, с точки зрения соответствия процессам в реальном самоподобном трафике, является предложенная модель на основе синтеза ансамбля квазипериодических источников и формализованных ON/OFF-состояний.

На основе разработанных математических моделей было проведено имитационное моделирование. Анализ статистических характеристик и оценка показателя Херста, синтезированных процессов подтвердили гипотезу о фрактальной природе трафика.

Характеристики указанных процессов дают возможность прогнозировать нагрузку в телекоммуникационных сетях. Результаты моделирования достаточно полно согласуются с результатами известных числовых и экспериментальных исследований.

Список литературы

1. Барвиненко В., Ланчев В. АСУ – проблемы и реше- ния // Воздушно-космическая оборона. – 2007. – № 7 (32). [Электронный ресурс]. – Режим доступа: www.vko.ru

2. Донсков Ю.Є., Ботнев А.К.. Системы связи и передачи данных армии США: состояние и перспективы развития // Военная мысль. – 2005. – № 7. – С. 4-47.

3. Семеріч Ю.П. Забезпечення зв’язку у миротворчих операціях // Наука і оборона. – 2004. – № 1. – С. 33-37.

4. Leland W., Taqqu M., Willinger W. On the self-similar nature of IP-traffic // IEEE/ACM Transaction on Networking. – 1997. – № 3. – P. 423-431.

5. Erramilli A., Narayan O., Willinger W. Experimental queuing analysis with long-range dependent packet traffic // IEEE/ACM Transaction on Networking. – 1996. – № 4. – P. 209-223.