Источник: «Компьютерный мониторинг и информационные технологии» — 2008 / Тезисы докладов IV Всеукраинской научно-технической конференции студентов, аспирантов и молодых ученых «Компьютерный мониторинг и информационные технологии» (КМИТ - 2008). — Донецк, ДонНТУ — 2008, с. 90.

 

 

АППРОКСИМАЦИЯ ТЕМПЕРАТУРНЫХ ПОКАЗАНИЙ СПОСОБАМИ ИНТЕРПОЛИРОВАНИЯ ИСХОДНЫХ ДАННЫХ

 

Е.А.Анастасова

Донецкий национальный технический университет

 

В наше время достаточно распространен процесс прогнозирования погодных условий. Известно, что для точного прогноза на определенный период времени необходим глубокий анализ показаний различных специализированных приборов. Возникает вопрос – возможен ли прогноз показаний температуры воздуха с помощью экстерполирования ограниченного количества исходных данных (т.е показаний, предшествующих данному моменту). Для выполнения данного задания был выбран математический пакет MATLAB 7.0 [1]. Суть процесса экстерполяции заключается в построении интерполяционного полинома по исходным данным (значениям функции в заданных точках), используя который возможно определяются значения функции в других, интересующих нас точках, лежащих вне рассматриваемого промежутка. Относительно интерполяции в рассматриваемом пакете реализована функция interp1. При выполнении работы был использован один из ее возможных синтаксисов:

yi = interp1(x,Y,xi,method)

где х – вектор значений по оси абцис, xi-узлы для интерполирования, y-значение функции в узловых точках, а «method» указывает один из подходов интерполяции данных, а именно:

·         “nearest” - аппроксимация кусочными полиномами нулевой степени (ступеньками): для любого промежуточного значения хi находится ближайшее табличное значение х, и в качестве значения уi берется соответствующее  табличное значение у;

·          “linear” – аппроксимация кусочными полиномами 1-й степени (ломаными);

·         “spline” – аппроксимация кусочнами полиномами 3-й степени (сплайнами);

·         “pchip” или “cubic” – аппроксимация кусочными полиномами Эрмита 3-й степени;

Существуют определенные рекомендации по использованию указанных процедур в зависимости от цели исследования. Так, например, для гладких данных предпочтительна процедура  “spline”, для негладких лучше использовать-“pchip” [2].

 Исходя из указанных особенностей перечисленных процедур, для проведения эксперимента были выбраны - “spline” и  “pchip”. В процессе вычислительного эксперимента варьировали длину массива исходных данных, их временной сезон и время суток.

Табл. 1 – Исходные данные

Была обнаружена некоторая закономерность, которую попытались проиллюстрировать на данных метеостанции №1 г. Донецка за период от 4.10.2004 до 6.10.2004 с шагом в 6 часов (табл. 1)

Эксперимент проводился следующим образом. Первоначально, было исключено последнее значение массива данных и определение его приближенного значения  по графику, построенному по 8 данным. После этого удаляются первые значения массива данных и, аналогично, наблюдаем изменение значения в исследуемой точке. В результате экспериментов получили, что существуют некоторые особенности прогнозирования в зависимости от исходных данных. Так, например, если выполняем прогноз с ночи на утро, то для наиболее точного значения необходимо 5 предшествующих точкек при использовании метода “spline” (погрешность ), либо – для метода “pchip” – необходимо задавать три точки (). Это связано с особенностями процедур (“pchip” строит более искаженный график) [3]. Для прогнозирования ночной температуры по вечерней и дневной – по утренним показаниям достаточно трех точек (в этом случае не наблюдалось значительных различий в приближенных значениях для двух методов ) (рис. 1, 2, 3). А для прогноза вечерней температуры по дневным ее значениям достаточным, оказалось, задание двух предшествующих точек ().

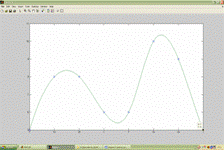
Рис. 1 – График по исходным данным (y=5)

 

                  

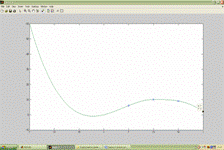
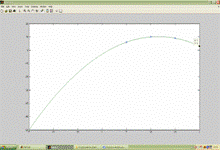
              Рис. 2 – Применение “spline” (y=3)               Рис. 3 – Применение “pchip” (y=2)

 

На основе выполненного эксперимента напрашивается вывод, что прогноз температурных показаний по предшествующим точкам возможен с погрешностью в 3. Однако при этом необходимо варьировать объем исходных данных и методы в зависимости от времени суток и сезона.

 

Литература

1.      www.mathworks.com/moler

2.      Ю.Кетков, А.Кетоков, М.Шульц. MATLAB 7.0 Программирование, численные методы.-СПб.:БХВ-Петербург,2005,-752с.:ил.

3.    “Numerical Computing with MATLAB”, 2007.-27