Авторы: Venkata Rama Prasad VADDELLA,
Ramesh Babu INAMPUDI
Перевод: Анастасова Е.А.
Источник: Journal of Applied Computer Science & Mathematics, no. 9 (4) /2010, Suceava. [Электронный ресурс] http://jacs.usv.ro/getpdf.php?paperid=9_3
Быстрое
фрактальное сжатие спутниковых и медицинских изображений основанное на энтропии
домен-ранг
Аннотация
Фрактальное сжатие изображений – это техника сжатия с потерями, которая была разработана в начале 1990-х годов. В его основе лежит использование свойства самоподобия, существующее в изображении, и поиск такого сжимающего аффинного отображения (фрактального преобразования), неподвижная точка которого близка к данному изображению в подходящей метрике. Большой интерес к этому подходу был вызван благодаря высокой степени сжатия с хорошим качеством декомпрессии, которыми характеризуется данная техника. Другим его преимуществом является то, что он обеспечивает возможность расшифровки изображения при более или менее высоких , по сравнению с оригиналом, уровнях разрешения без заметного ухудшения качества. К числу недостатков подобного рода алгоритмов следует отнести значительное время кодирования. В данной работе, с целью снижения времени кодирования и сохранения уровня погрешности и степени сжатия, предлагается метод быстрого фрактального сжатия, основанный на анализе энтропии домен-ранг и предполагающий выполнение двух этапов. Первоначально, области с близкими дисперсиями, исключаются из набора доменов, затем, во время кодирования, сравниваются только домены и ранги, имеющие близкую энтропию. В результате такого подхода, многие заведомо не подходящие домены не принимают участия в подборе пары, что значительно сокращает общее время кодирования. Метод применялся для сжатия спутниковых и медицинских изображений (512x512, 8-бит серой шкалы) и экспериментальные результаты его применения показали, что он дает более высокую производительность по сравнению с поиском лучшего домена, основанного на классификации по методу Фишера.
Ключевые слова: Фрактальное сжатие изображения, энтропия домен-ранг, алгоритм квадро-дерева, поиск с помощью вектора характеристик.
Цифровые изображения,
связанные со спутниковым дистанционным зондированием характеризуются как изображения
с высокой информативностью [1,2]. Большие объемы данных требуют больших массивов
памяти для их хранения и вызывают длительное
время передачи. Для решения этих
проблем активно используются алгоритмы сжатия данных . Оцифрованные медицинских изображений имеют большое число пикселей с почти одинаковой интенсивностью, многие
из которых формируют однородные
регионы [3,4,5]. Гистограмма, как правило, выявляет один или два больших пика (как правило, при низкой интенсивности), а также только
небольшое количество пикселей по всему динамическому диапазону. Фрактальные методы могут быть использованы для сжатия гладких областей обеспечивая высокую степень
сжатия и высокое
качество восстановленного изображения. Модель систем частично
итерируемых функции хорошо подходит для гладких областей изображения, но при обработке районов со сложными текстурами, отдельные детали могут
быть потеряны даже при относительно низкой степени сжатия.
Базовая схема
фрактального алгоритма сжатия изображения начинается с разбиения исходного
изображения на непересекающиеся блоки размером rxr, называемые рангами, и формирования
пула доменов состоящего из всех возможных пересекающихся блоков, называемыми
доменами, в том числе 8 изометрий (отражение и вращение) [6]. Для каждого ранга
подбирается лучший домен, обеспечивающий наименьшую погрешность RMS после применения к
области блока сжимающих аффинных преобразований. Уравнение фрактального сжатия для
конкретного ранга содержит коэффициенты сжатия, смещения яркости, положение
наилучшего домена и его изометрии [7]. Задача декодирования заключается в
поиске неподвижной точки, декодированного изображения, начиная с любого
начального изображения.
Данная процедура применяется ко всем доменным и ранговым блокам, пока не будут получены все декодированные ранговые блоки. Процедура поиска повторяется, пока не будет достигнута сходимость. Проблемой фрактального сжатия является высокая вычислительная сложность и нахождение лучшей пары домен-ранг [8]. Наиболее привлекательным свойством является то, что изображение может быть декодировано до необходимого размера, т.о. степень сжатия может возрастать экспоненциально [9].
Однако, перебор всего набора доменов требует серьезных вычислений. Для изображения размера nxn, число рангов составляет (nxn/rxr) и число доменов - (n-2r+1)x(n-2r+1). Вычислительная сложность поиска наилучшего соотношения между рангом и доменом представляет O (r2). Если r это константа, то вычислительная сложность полного перебора представляет O (n4).
II. Степень исследования проблемы
Ирвинг Фишер [10] предложил алгоритм квадро дерева для разделения изображения на ранги и домены для фрактального алгоритма сжатия. В этом алгоритме, ранги и домены разделяются на 3 главных класса, основываясь на среднем значении пикселей в четырех квадрантах блоков. В дальнейшем они разделяются на 24 подкласса (!4), основываясь на значении дисперсии в четырех квадрантах. Таким образом, все домены и ранги подразделяются в общем на 72 класса. Этот алгоритм называет алгоритмом поиска по классификациям, т.к. сравниваются домены и ранги, которые относятся к определенному классу. Но, из-за большого количества доменов, время кодирования очень велико. Одним из простых способов разрешения этой проблемы это уменьшение количества доменов, входящих в пул.
Это достигается путем введения пространственных ограничений использования набора доменов для каждого ранга [8]. Принимая во внимание, что для обеспечения сжатия значыение дисперсий домена должно быть более высоким, чем значение дисперсии ранга, домены с низкой дисперсией могут быть исключены из области бассейна [11]. Кроме того, набор доменов может сокращаться, за счет исключения доменов, которые находятся в подобном отношении с другими областями в бассейне [12]. В течение последнего десятилетия ряд исследователей предложили методы, для уменьшения размера набора доменов, основанные на различных функциях разделения на домены и ранги [13]. Значение дисперсии использовалось как показатель для уменьшения размера набора доменов [11,14,15]. В последнее время в качестве характеристической функции для фильтрации доменов было предложено использовать значение энтропии [16]. Томас Зумбакис и Янас Валантинас [17] предложили подход для улучшения времени кодирования, основанный на классификации набора рангов и доменов исходя из постоянства их значений в частной области. Даниэль Риччио и Мишель Наппи [18] предложили метод для сокращения времени кодирования, ранжируя домены и ранги по отношению к показателям энтропии заданной области. В последнее время был предложен метод на основе выделения признаков [19]. В этой схеме весь процесс подбора подходящих доменов основан на погрешности аппроксимации.
III. Предлагаемый метод
В данной работе представлен новый метод, для сокращения времени кодирования основанный на вычислении энтропии доменов и рангов. Сравнение между рангом и доменом на совпадение происходит только тогда, когда разность энтропии меньше, чем заданный порог ошибки λdepth. Для разбиения изображения на ранги и домены используется алгоритм квадро-дерева. Домены и ранги классифицируются на основе значений дисперсий и среднего. Изначально, исходное изображение разбивается на перекрывающиеся области Di, (размером 2rx2r), для каждого раздела квадро-дерева, где rxr - размер рангов Ri. Шаг для домена задается как δh= δv=4 в горизонтальном и вертикальном направлениях. Домены классифицируются на основании среднего значения и дисперсии пикселей четырех квадрантов блока [10]. Пул доменов D образуется путем размещения всех доменных блоков Di по отдельным спискам в соответствии с классом. Поиск лучшей пары домен-ранг заключается в сжатии каждого домена до размера блока в среднем до 2x2 пиксел. Во время кодирования также могут классифицироватся ранги Ri. Поиск подходящего домена Di состоит из перебора пула доменов D, и коэффициентов аффинного преобразования Wi, которое сводит к минимуму среднеквадратичное отклонение между Ri и трансформированного w.Di, (т.о. wi.Di ≈ Ri). Целью является снижение размерности, для ранга с количеством пикселей n, каждый с яркостью ri, и уменьшенного домена состоящего из n пикселей, каждый с яркостью di.
![]()
Это задает настройки для значения масштабирования S и яркости O, которые необходимы, чтобы значения аффинных преобразований Di имели как минимум расстояние в квадрат от Ri. Минимальное значение E имеет место, когда частные производные по S и O равны нулю. Решение полученных уравнений даст коэффициенты S и О.
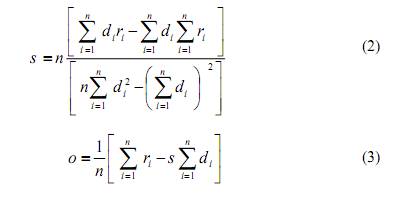
Таким образом, E (Ri, Di) вычисляется по формулам:

Среднеквадратичная ошибка вычисляется следующим образом:

А. Энтропия
Пусть множество дискретного набора символов {v0, v1,…,vk} с соответствующими вероятностями pi. Энтропия [20] дискретного распределения показывает меру случайности обращаемости к последовательности символов, и определяется по формуле:
![]()
В обработке изображений, отдельные результаты p0, p1…,pk, представляют нормированную частоту появления каждого уровня серого в изображении. Это отображает пространственная информация, т.е. распределение уровней серого в изображении (гистограмма). Для блока изображения, энтропия определяется следующим образом:

где, k - максимальное количество уровней серого в данном изображении.
В. Алгоритм, основанный на энтропии
Аффинное преобразование, примененное к доменному блоку не меняет значение его энтропии [21]. Два блока изображения домен и ранг связанные аффинным преобразованием будут иметь равные значения энтропии. На основе данного свойства, предлагается быстрый алгоритм фрактального сжатия. Исходное изображение I размером nxn (8 bit gray scale) разбито на перекрывающиеся доменные блоки Di размером 2rx2r. Во время кодикования, изображение разбивается на неперекрывающиеся ранговые блоки Ri размером rxr. Абсолютная разница значений энтропии доменного Di и рангового блока Ri вычисляется по формуле:
│Entropy (Ri) – Entropy (Dj) │ ≤ λdepth, (9)
Доменные и ранговые блоки удовлетворяющие условию указанному выше, подвергаются линейной регрессии, т.е. сравнивая ошибки rms с заданной погрешностью Ec, выявляется лучшая пара домен-ранг.
С. Адаптивный порог ошибки, λdepth
Сформулированный в данной работе адаптивный порог ошибки λdepth, применяется на каждом шаге алгоритма квадро-дерева для сравнения значения энтропии доменов и рангов. На этапе алгоритма квадро-дерева соответствующего минимальному min_part, λ0 принимается как начальное значение (в данной работе, 0.7). На других этапах квадро-дерева, λ рассчитывается по формуле,
λdepth = λdepth-1+(depth-1) (10)
Данная формула получена путем выполнения повторяющихся экспериментов над изображениями различных размеров и текстур, тестирования на оптимальное время кодирования, качество и степень сжатия. Было отмечено, что для рангов на высоких уровнях работы алгоритма (ранги самого малого размера), должно быть обработано большое количество доменов, в то время как для рангов на начальных этапах работы алгоритма достаточно обработать значительно меньшее количество доменов для выполнения достаточного совпадения.
IV. Схема алгоритма кодирования
Шаг 1: Образовать наборы доменов Ddepth, в соответствии с каждым уровнем квадро-дерева, начиная с минимального уровня до максимального (depth=0 до max_part- min_part).
Шаг 2: Расчет энтропии доменных блоков в каждом бассейне Ddepth.
Шаг 3: Классификация и сортировка областей в каждом бассейне Ddepth в порядке возрастания энтропии в списке структуры.
Шаг 4: Удаление близких областей (с почти равными значениями дисперсии) из списка.
Шаг 5: Поиск лучших совпадения между всеми рангами и доменами одного класса, используя следующую процедуру.
Write_header_info;
(min_part, max_part, domain_step, hsize, vszie)
depth=0; ec =
rms_tol;
Function Quadtree (image, depth) {
best_rms=infinity; λ0=initial value;
λdepth= λdepth-1+(depth-1);
While (depth<min_part) Quadtree (image, depth+1);
set
R1 =
I2 and
mark it uncovered.
While there are uncovered ranges Ri do {
//Select the domain pool list Ddepth to
//corresponding to current range block Ri.
for
(j=1;j<num_domains; ++j) {
If │Entropy (Ri) – Entropy (Dj) │ ≤ λdepth, {
Compute s, o, and sym_op;
Compute E (Ri, Di);
If E (Ri,Di ) ≤
best_rms {
best_rms= E(Ri, Di );
best_domain=(domain_x,domain_y);
}
}// end for
If (best_rms>ec) && (depth<max_part) Quadtree (image,
depth+1);
Else
Write_transformations(best_domain,s,o,sym_op);
}//end while
}// end function Quadtree( )
V. Полученные результаты
Эксперименты были проведены на INSAT метеорологических изображениях и изображениях снимка КТ мозга (512x512, 8 бит серого). Полученные результаты приведены в таблице и сделано сравнение с метод Фишера [10].
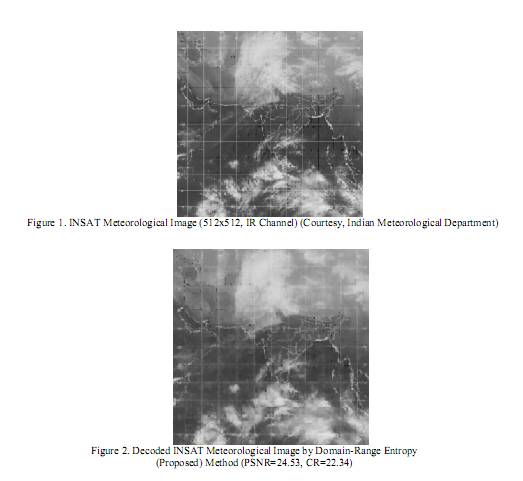
На Рисунке 1 показано исходное метеорологическое изображение INSAT (512x512, ИК-канал) и 2 два изображения - результаты работы описанного алгоритма: сжатое и декодированное изображения.
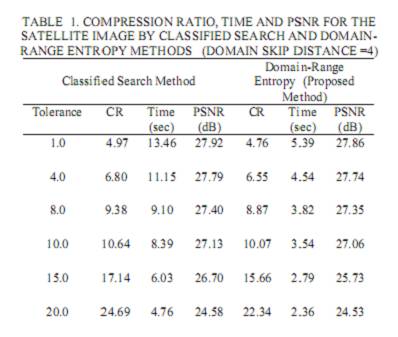
В Таблице 1 отображена степень сжатия, время и PSNR для изображения спутника обработанного путем перебора с помощью классового алгоритма и энтропии домен-ранг.
На Рисунке 3 показано исходное изображение снимка КТ мозга (512x512) и Рисунок 4 показывает сжатое и декодированное изображения с помощью предложенного метода. Таблица 2 показывает коэффициент компрессии, время и PSNR полученные в результате обработки снимка КТ мозга с помощью алгоритма разбиения на классы и предложенного метода.
На рисунках 5 и 6 показаны результаты
работы предложенного метода, который дает превосходную производительность с точки зрения
сокращения времени кодирования, при этом достигается аналогичный уровнь погрешности PSNR и сжатия по сравнению с методом поиска путем разбиения
на классы.
Значения, предназначенные для различных параметров:
1. 5 бит используются для квантования коэффициента масштабирования S, и 7 бит для смещения О.
2. Для всех изображений, максимальный размер диапазона 16x16 (минимальная глубина дерева Quad 5), а минимальный размер диапазона 4x4 (максимальная глубина дерева Quad 7). Используются три уровня Quad дерева.
3. Бассейн доменов построен с дистанцией, H = 4 и V = 4, т. е. расстояние между соседними областями составляет 4 пикселя.
4. RMS допустимой погрешности, ЕС является вводимые значения 1,4,8,10,15 и 20, что дает результаты, начиная от низкого до высокого коэффициентов сжатия.
А. Параметры кодирования (общие для всех изображений)
Размер изображения: 512x512 (8 битв градациях серого)
Количество разделов дерева = 3
В. Общее количество доменов
Вычисляются три различных по размеру области, в соответствии этапами алгоритма Quad дерева.
Размер 32х32 = ((512-32) / 4 +1) * ((512-32) / 4 +1) = 14.641
Размер 16х16 = ((512-16) / 4 +1) ((512-16) / 4 +1) = 15.625
Размер 8x8 = ((512-8) / 4 +1) * ((512-8) / 4 +1) = 16.129
Общее количество доменов во всех разделах = 46395
Для предложенного метода значение адаптивного параметра λdepth присваивается начальное значение, λ0 = L.25, и для других глубины дерева четверых,
λdepth = λdepth-1+ (depth-1) (11)
Алгоритм реализован на языке С, с VC ++6.0 компилятор, на персональном компьютере с процессором Intel Centrino Duo T2250,тактовая частота 1,73 ГГц, 2 Гб оперативной памяти.



VI. Выводы
В работе, предложен улучшенный алгоритм фрактального сжатия,основанный на анализе уровня энтропии пары домен-ранг. Алгоритм был проверен на спутниковых и медицинских изображениях (512x512, в оттенках серого), так как эти изображения, как ожидалось, позволят получить высокую степень сжатия, вследствие гладкости их описывающих функций. Проведенные эксперименты показали, что предложенный подход существенно сокращает время кодирования по сравнению с классифицированным методом Фишера [6]. Было показано, что восстановленные изображения практически совпадают с оригинальными. В будущем, предполагается выполнение алгоритма осуществлять на параллельных многопроцессорных машинах или с помощью PVM и MPI модулей программного обеспечения. Авторы работы апробировали также реализацию структур данных с помощью построения деревьев поиска, однако, эта методика дала значительно худшие результаты ,в связи с тем, что на создание поисковых деревьев уходило много времени.