
Рис. 1. Классификация алгоритмов моделирования
Источник: http://iuskm.donntu.ru/electronic/Том_2/Секция_7.pdf
Попов Ю.В., Балута А.В. Классификация методов динамической балансировки нагрузки при распределенном логическом моделировании. Рассмотрены принципы организации вычислительных систем для распределенного логического моделирования цифровых систем. Определены причины появления несбалансированной нагрузки. Получена классификация методов и алгоритмов динамической балансировки нагрузки в распределенных вычислительных системах.
Высокая размерность и сложность логических схем требует больших затрат вычислительных ресурсов и времени при моделировании. Увеличить производительность системы моделирования можно при использовании нескольких компьютеров, соединенных в локальную вычислительную сеть [1]. При этом возможно появление неравномерной нагрузки на компьютеры в сети, приводящее к уменьшению скорости моделирования.
Предмет исследования – вычислительные системы для распределенного логического моделирования цифровых систем. Объект исследования – методы и алгоритмы балансировки нагрузки в распределенных вычислительных системах. Цель исследования – классификация методов балансировки нагрузки в распределенных вычислительных системах. Задачи исследования – рассмотрение и сравнение существующих методов получения сбалансированной нагрузки при распределенном логическом моделировании.
В [2] предлагается использование коммуникационных логических процессоров. В [3] рассматриваются методы динамической балансировки нагрузки в системе Triad.Net. В [4] сформулированы правила, согласно которым должно производиться изменение топологии связей при моделировании в консервативном протоколе синхронизации. В [5] рассмотрены принципы организации системы контроля нагрузки для мультикластерных систем моделирования с оптимистическим управлением временем.
Изменения, которым подвергается система моделирования, оформляются в виде событий и состояний. Текущие значения в узлах схемы – это состояния системы, а изменения сигналов во времени – события. Моделирование выполняется в дискретном виртуальном времени [1]. Алгоритмы моделирования различаются порядком обработки и планирования новых событий (рис. 1).
При последовательном моделировании используется один компьютер. При параллельном моделировании ускорение достигается за счёт того, что отдельные части алгоритма моделирования выполняются параллельно [1]. При распределенном моделировании используется несколько отдельных компьютеров, объединенных в сеть. При этом моделируемая система разделяется на множество отдельных частей, каждая из которых моделируется на отдельном компьютере (моделирующем процессоре – МодПр). При этом возникает проблема синхронизации работы МодПр в сети.

|
Рис. 1. Классификация алгоритмов моделирования |
Наиболее простой способ синхронизации МодПр – использование глобального виртуального времени (синхронное распределенное моделирование). В асинхронных алгоритмах каждый МодПр выполняется в локальном виртуальном времени LVT.
Консервативный алгоритм моделирования обеспечивает выполнение событий в строго хронологическом порядке. В оптимистических алгоритмах МодПр не ожидают разрешения на обработку событий, допустимым является появление событий в локальном прошлом, при этом производится возврат системы к предыдущему состоянию. При использовании комбинированных протоколов МодПр обрабатывают события, запланированные на моменты времени от LVT до LVTH+∆t, где 0<=∆t<=+∞ - определяет степень оптимистичности протокола, при ∆t=0 комбинированный протокол синхронизации становится консервативным, а при ∆t=+∞ - оптимистическим [1].
Система моделирования представляет собой набор взаимосвязанных логических процессоров (ЛП). Изменения состояний системы - это события с временными метками.
Сфера влияния события – это та часть моделируемой системы, для которой при выполнении данного события происходят изменения [2]. Сфера влияния для некоторого ЛП в интервале времени [t1;t2], S(ЛПi, [t1;t2]) - объединение сфер влияния сгенерированных в этом интервале времени событий [2]. Пересечение сфер влияния каждого события позволяет получить частичный порядок (или очередь) для множества переменных состояний в интервале времени [t1; t2], в котором переменные, к которым обращались чаще всего, находятся в начале очереди [2]. Любой подход к декомпозиции и распределению общедоступных переменных, должен учитывать этот порядок [2].
В системе моделировании используется дополнительный набор коммуникационных логических процессоров (КЛП). В функции КЛП входит определение случаев пересечения сфер влияния и обеспечение равномерной нагрузки на подчинённые ЛП. В начале все общедоступные состояния управляются одним КЛП (рис. 2).
Связь между ЛП отсутствует, данные между ними передаются через КЛП. Если, например, необходимо передать данные между двумя ЛП, которые не связаны одним КЛП, то данные будут передаваться вверх по дереву связей КЛП. При моделировании производится сбор статистики, и определяется, между какими группами ЛП происходит наиболее частый обмен данными, тогда для них можно добавить отдельный КЛП, что уменьшит нагрузку на остальные КЛП. Система моделирования имеет древовидную структуру, где ЛП – листья, КЛП – промежуточные узлы дерева [2] (рис. 3).
Ранг переменной vj для процесса ЛПi в интервале [t1;t2] - r(vj, ЛПi, [t1;t2]) – это количество событий, относящихся к сфере влияния vj [2]. Стоимость доступа переменной vj к логическому процессу ЛПi – это количество КЛП, которые должны быть пройдены, чтобы достигнуть vj в интервале времени [t1;t2]. Стоимость обращения к локальным переменным l(vj, ЛПi) в своём КЛП равна 0.
 |
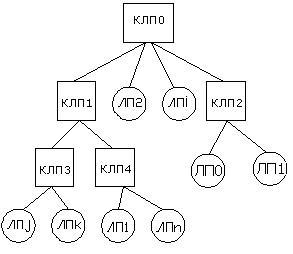 |
Рис. 2. Начальное распределение |
Рис. 3. Генерация дерева КЛП |
 |
(1) |
Стоимость доступа одного ЛП ко всем переменным в сфере влияния S(ЛПi) определяется по формуле (1). Общая стоимость доступа ко всем ЛПi, i=1..n всех ЛП данного распределения в интервале времени [t1;t2] определяется по формуле (2). Наилучшее распределение в интервале [t1;t2] имеет минимальную общую стоимость [2].
 |
(2) |
В [3] рассматриваются принципы реализации подсистемы балансировки в системе моделирования Triad.Net. Задача балансировки нагрузки представляется как задача отображения неизоморфных связных графов: TM > NG, где TM – множество графов моделей, NG – множество графов конфигураций компьютерной сети. Граф G NG, G = {C, Ed}, определяется множеством вычислительных узлов C и ребер Ed как линии связи.
NG, G = {C, Ed}, определяется множеством вычислительных узлов C и ребер Ed как линии связи.
Рассматриваются три разновидности задачи балансировки [3]: статическая Bs, динамическая (автоматическая) Ba и динамическая (управляемая) Bc. Алгоритм Bs выполняется до начала моделирования и основывается на анализе структуры моделируемой системы: выявляются клики в графе модели и они отображаются на одном вычислительном узле. В алгоритме Ba графы G и M рассматриваются как нагруженные [3]. Для нахождения лучшего распределения моделируемой системы по вершинам графа G используя генетические алгоритмы. Алгоритм Bc использует экспертную компоненту на основании правил оптимизации и нестандартные информационные процедуры [3].
В консервативных алгоритмах не может обрабатываться сообщение с временной меткой t (и поэтому блокируется процесс, который не может отправить сообщение), пока не обработаны все сообщения с временной меткой меньше t [4]. Наименьшее входное время (EIT) ЛП – это время выполнения самого раннего события. ЛП может обрабатывать только те события, время наступления которых меньше EIT [4]. Наименьшее выходное время (EOT) для ЛП соответствует времени события с наименьшей временной меткой, отправляемого другому ЛП, EOT = EIT + предсказание. Величина предсказания указывает на то, что в данном временном интервале у ЛП не появится исходящих событий. EIT = min(EOT), получаемых по всем входным каналам связи. При создании новых связей должны учитываться некоторые особенности [4]. Пусть, например, уже существует канал связи от А к B и от A к C и создается новая связь от B к С. Для того чтобы исключить нарушение порядка обработки сообщений, если сообщение с наименьшей временной меткой по каналу связи от B к C имеет время t, в системе моделирования должны выполняться условия [4]:
- B должен добавить C в множество приемников в момент времени не более чем t;
- C должен добавить B в множество источников в момент времени не более чем t.
Оптимистический алгоритм синхронизации позволяет существенно сократить время моделирования [5]. Однако при необходимости выполнения отката на ЛП должен производиться перерасчёт всей части схемы, даже если в итоге необходимо пересчитать небольшое число элементов. В [5] предлагается два метода решения данной проблемы: мультикластерное представление моделируемой на ЛП части схемы (рис. 6) и механизм контроля нагрузки, выполняющий перемещение кластеров при моделировании (рис. 7).
При моделировании производится оценка текущей загрузки ЛП. Виртуальное время продвижения VTP – величина, обратная значению загрузки. Вначале определяется интегрированное виртуальное время IVT (3) для каждого ЛП с множеством кластеров на каждом шаге моделирования S [5]. Виртуальное время продвижения VTP для одного ЛП в интервале времени [t1; t2] определяется по формуле (4). Далее вычисляется время безубыточности tBE [5]. Процедура балансировки выполняется при условии (5).
 |
 |
| Рис. 6. Мультикластерное разделение | Рис. 7. Механизм контроля |
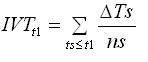 |
(3) |
 |
(4) |
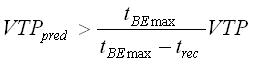 |
(5) |

|
| Рис. 9. Классификация методов балансировки нагрузки |
Рассмотрены принципы организации систем логического моделирования. Получена классификация методов обеспечения равномерной загрузки на компьютеры в системах распределенного логического моделирования.
В дальнейшем планируется поиск и программная реализация оптимального решения проблемы неравномерной нагрузки на вычислительные узлы распределенной системы моделирования с использованием рассмотренных методов. Планируется провести исследование полученной реализации для различных моделируемых цифровых систем.
1. Ладыженский Ю.В., Попов Ю.В. Программная система для исследования протоколов синхронизации при распределенном событийном логическом моделировании // Материалы научно-практической конференции «Современные технологии проектирования систем на микросхемах программируемой логики».- Харьков: Харьковский национальный университет радиоэлектроники, 2003. – С.44.
2. Theodoropoulos G., Logan B. An approach to interest management and dynamic load balancing in distributed simulation // 2001 European Simulation Interoperability Workshop.- London: University of Westminster, 2001. – p.566-571.
3. Миков А.И.., Замятина Е.Б., Осмехин К.А. Метод динамической балансировки процессов имитационного моделирования // Материалы Всероссийской научно- технической конференции «Методы и средства обработки информации МСО-2005».- Москва: МГУ, 2005.- с.472-478.
4. Jha V., Bagrodia R. Transparent Implementation of Conservative Algorithms in Parallel Simulation Languages // 1993 Winter Simulation Conference.- New York: ACM, 1993.- p.677-686.
5. Schlagenhaft R., Ruhwandl M., Sporrer C., Bauer H. Dynamic load balancing of a multi-cluster simulator on a network of workstations // 9th Workshop on Parallel and Distributed Simulation.- New York: Parallel and Distributed Simulation, Workshop on, 1995.- p. 175-180.