МЕТОД УПРАВЛЕНИЯ ИНТЕРЕСАМИ И ДИНАМИЧЕСКАЯ БАЛАНСИРОВКА
НАГРУЗКИ ПРИ РАСПРЕДЕЛЕННОМ МОДЕЛИРОВАНИИ

Georgios Theodoropoulos, Brian Logan

Перевод с английского: Балута А.В.

Источник: Статья на портале электронной научной библиотеки CiteSeerx
http://www.cs.nott.ac.uk/~bsl/papers/esiw01.pdf

АННОТАЦИЯ

   В данной статье обсуждается распределенное моделирование систем с большим количеством общедоступных состояний и вопросы, связанные с управлением сферами влияния и динамической балансировки нагрузки. Предлагается эффективное распределение общедоступных состояний как ключевая проблема при моделировании за счёт использования многоуровневой иерархической схемы управления сферами влияния для облегчения динамической балансировки нагрузки.

1 Введение

   Различные подходы к использованию параллелизма и нескольких отдельных уровней в моделировании уже были изучены ранее (Ferscha & Tripathi 1994). Парадигма использования логических процессоров разделяет имитационную модель на сеть параллельных Логических Процессов (ЛП), каждый из которых моделирует некоторый объект(ы) или процесс(ы) в моделируемой системе. Каждый ЛП обрабатывает часть пространства состояний системы, и изменения состояния системы оформлены как события с временными метками.

   С точки зрения ЛП различают два типа событий; а именно, внутренние события, которые оказывают влияние только на переменные состояния ЛП, и внешние события, которые могут также оказать влияние на переменные состояния других ЛП. Внешние события оформляются как сообщения с временными метками, которыми обмениваются взаимосвязанные ЛП. Цель этого взаимодействия состоит в том, чтобы обмениваться информацией относительно значений переменных состояния, которые имеют общие интересы на ЛП, которые взаимосвязаны (общедоступные состояния). Для систем, моделирующих сложные динамические процессы трудно правильно определить соответствующую топологию моделирования до начала моделирования. В таких системах существует большое множество общедоступных переменных состояния, к которым можно было, в принципе, обратиться или которые должны быть обновлены в процессе моделирования. Инкапсуляция общедоступных состояний в одном процессе (через некоторую централизованный сервис) может приводить к тому, что все ЛП будут простаивать, ожидая ответа от перегруженных ЛП. Распределение общедоступных состояний, в свою очередь, будет часто приводить к передаче сообщений от всех ЛП ко всем остальным, что может привести к чрезмерной загрузке сети.

   Новое решение основано на использовании сфер влияния, которые предназначены для того, чтобы динамически анализировать и перераспределять общедоступные состояния для избавления от централизованных сервисов и уменьшения количества передач по сети.

4 Новое решение

   Полагается, что каждый ЛП создаёт и обрабатывает конечное число типов сообщений. Различные типы сообщений могут по-разному воздействовать на остальные ЛП, и сообщения определенных типов будут воздействовать только на определенные переменные состояния (а значения остальных переменных останутся прежними).

4.1 Сферы влияния

   Сфера влияния для каждого события – это множество переменных состояния, читаемых или обновляемых как следствие события. Сфера влияния зависит от типа события. Сфера влияния ограничена непосредственными и предсказуемыми эффектами от выполнения события, зависящими от текущей конфигурации системы моделирования и от действий других ЛП в ответ на это событие.

   Сферы влияния можно использовать для каждого ЛП, чтобы получить идеальное распределение общих состояний. Определение сфер влияния для каждого ЛП - pi в интервале времени [t1,t2], s(pi, [t1,t2]) как объединение сфер по сгенерированным в этом интервале времени событиям. Пересечение сфер влияния для каждого события, сгенерированного в процессе моделирования, позволяет получить частичный порядок (или очередь) для множества переменных состояний в течение интервала времени [t1,t2], в котором переменные, к которым обращались чаще всего, находятся в начале очереди. Этот полученный частичный порядок может использоваться как мера загрузки физических процессоров. Переменные состояния, находящиеся в начале очереди, требуют большего числа процессоров, а для переменных, находящихся в конце очереди, достаточно лишь одного процессора.

   Любой подход к декомпозиции и распределению общедоступных переменных, должен учитывать этот порядок. Однако любая реализация может только приблизиться к этой идеальной декомпозиции. Кроме того, этот частичный порядок изменяется со временем, так как будут изменяться переменные состояния и число событий, и каждая реализация должна учитывать стоимость реорганизации дерева, отображающего новое распределение. Также необходимо уменьшить количество коммуникаций из-за их высокой стоимости передачи.

4.2 Динамическое распределение состояний и балансировка нагрузки

   Декомпозиция состояний достигается путём введения дополнительного набора логических процессоров – коммуникационных логических процессоров (КЛП). КЛП выполняют функции управления интересами.
   В функции КЛП входит:

обеспечение равномерной нагрузки на подчинённые ЛП, путем принятия соответствующих решений.

   Перераспредление общедоступных состояний выполняется динамически, вследствие событий, возникающие в логических процессах в процессе моделирования. Таким образом, количество КЛП и их распредление не фиксировано и может изменяться при моделировании.

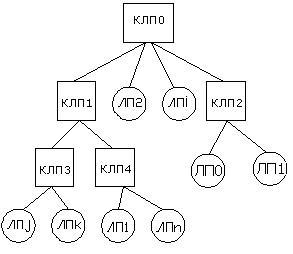
   В начале все общедоступные состояния управляются одним КЛП, как показано на рисунке 1(а). Все сообщения, генерируемые на ЛП, передаются через единственный КЛП, который выполняет все функции, обеспечивающие связь между всеми КЛП.

   При моделировании производится сбор статистики: между какими группами ЛП происходит наиболее частый обмен данными, тогда для них можно добавить отдельный КЛП, что уменьшит нагрузку на остальные КЛП. Величину этой загрузки можно определять исходя из некоторого предопределенного значения (например, число сообщений за некоторый период времени). В повторяющемся процессе создания новых КЛП проверяется загрузка и требуется, чтобы сохранялась полная загрузка на КЛП в пределах заданных границ (рисунок 1(б)).

(a)	(б)

Рисунок 1: Генерация дерева КЛП

   Эта стратегия приводит к древовидной структуре, где ЛП – листья, КЛП – промежуточные узлы дерева. Если, например, необходимо передать данные между двумя ЛП, которые не связаны одним КЛП, то данные будут передаваться вверх по дереву связей КЛП.

   Ранг переменной vj для процесса ЛПi в интервале времени [t1,t2], r(vj,ЛПi,[t1,t2] – количество событий, в сферу влияния которых входит переменная vj. Стоимость доступа логического процессора ЛПi к переменной vj (ранг vj для ЛПi - r(vj, ЛПi)) – это количество КЛП, которые должны быть пройдены, чтобы достигнуть изменения vj в интервале времени [t1;t2]. Стоимость обращения к локальным переменным l(vj, ЛПi) в собственном КЛП равна 0. Стоимость доступа некоторого ЛП ко всем переменным в сфере влияния S(ЛПi) определяется так:

   Общая стоимость доступа ко всем ЛПi, i=1..n всех ЛП конкретного распределения в интервале времени [t1,t2]:

   Наилучшей декомпозицией в интервале времени [t1;t2] является та, при которой общая стоимость является минимальной.

   При изменении очереди по сферам влияния соответственно должна изменяться структура дерева, вычислительная нагрузка на узлы которого должна быть сбалансированной. Это достигается двумя способами [2]: изменением позиции ЛП в дереве, либо перемещением состояний. Состояние может быть перемещено либо переносом подмножества переменных состояний от одного КЛП к другому, либо объединением КЛП, которые находятся выше по иерархии и их повторным разбиением.

5 Нерешенные проблемы

   Рассмотрим пример перераспределения дерева КЛП. Пусть необходимо осуществить перемещение ЛП1 в дереве, поскольку происходит частое обращение к нему КЛП2 (Рисунок 2(а), 2(б)). Если это уменьшит загрузку, то можно переместить LP0 в CLP0 (Рисунок 2(в)). Возможен альтернативный вариант – перемещение множества переменных состояний LP1 и CLP2 в CLP1.

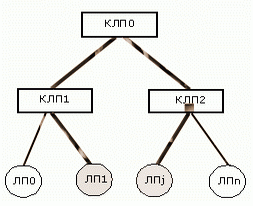(а)

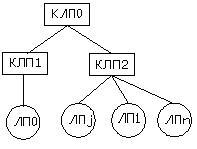(б)

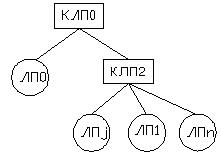(в)

Рисунок 2: Перемещение ЛП и объединение КЛП

   Предложенная архитектура может поддерживаться для консервативных и оптимистических протоколов синхронизации.

Литература

1. Babaoglou, O. & Marzullo, K. (1993), Consistent global states of distributed systems: Fundamental concepts and mechanisms, Technical Report UBLCS-93-1, Laboratory for Computer Science, University of Bologna.
2. Berrached, A., Beheshti, M., Sirisaengtaksin, O. & de Korvin, A. (1998), Alternative approaches to multicast group allocation in HLA data distribution, in ‘Proceedings of the 1998 Spring Simulation Interoperability Workshop’.
3. Burdorf, C. & Marti, J. (1993), ‘Load balancing strategies for Time Warp on multi-user workstations’, The Computer Journal 36(2), 168–176.
4. Calvin, J. O., Chiang, C. J. & Van Hook, D. J. (1995), Data subscription, in ‘Proceedings of the Twelfth Workshop on Standards for the Interoperability of Distributed Simulations’, pp. 807–813.
5. Carothers, C. & Fujimoto, R. (1996), Background execution of Time-Warp programs, in ‘Proceedings of 10th Workshop on Parallel and Distributed Simulation’, Society for Computer Simulation, Society for Computer Simulation.
6. Chandy, K. M. & Lamport, L. (1985), ‘Distributed snapshots: Determining global states of distributed systems’, ACM Transactions on Computer Systems 3(1), 63–75.
7. Def (1998), High Level Architecture RTI Interface Specification, Version 1.3.
8. Ferscha, A. & Tripathi, S. K. (1994), Parallel and distributed simulation of discrete event systems, Technical Report CS.TR.3336, University of Maryland.
9. Glazer, D. W. & Tropper, C. (1993), ‘On process migration and load balancing in Time-Warp’, IEEE Transactions on Parallel and Distributed Systems 3(4), 318–327.
и т.д.