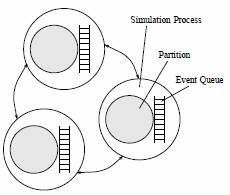
Рисунок 1. Одна часть на моделирующем процессоре
Источник: Статья на портале электронной научной библиотеки CiteSeerx
http://citeseerx.ist.psu.edu/viewdoc/summary
Алгоритмы Time Warp очень чувствительны к изменениям доступной вычислительной мощности. Статья содержит два метода, применимых при моделировании СБИС с использованием Time Warp, позволяющих уменьшить отрицательный эффект неидеальной среды выполнения при параллельном моделировании. Алгоритм динамической балансировки нагрузки адаптирует процесс моделирования при изменениях доступной мощности обработки. Технология мультикластерного разделения позволяет значительно улучшить производительность систем, базирующихся на Time Warp алгоритмах c неоднородными вычислительными сетями.
Из-за увеличивающейся сложности цифровых схем логическое моделирование вынуждено потреблять большое количество процессорного времени и памяти. Время моделирования часто превышает дни, и требуемые объемы памяти часто лежат за пределами обыкновенных рабочих станций. Методы параллельного и распределенного моделирования позволяют решить обе эти проблемы. Time Warp – это известный оптимистический протокол синхронизации для параллельного моделирования, позволяющий достигать значительного уменьшения затрачиваемого времени. Все-же, при детальном анализе полученных результатов видно, что в алгоритмах большая часть времени моделирования тратится на откаты. Поэтому главная цель исследования – уменьшить время, необходимое для откатов.

|
Рисунок 1. Одна часть на моделирующем процессоре |
При моделировании используются логические процессоры (ЛП), которым отводится некоторая часть схемы (может содержать от 1000 до 100.000 элементов-вентилей). Недостаток: всякий раз, когда необходимо производить откат, должен быть произведен пересчёт всей части схемы, даже если откату должны подвергнуться только несколько элементов. Как следствие - трата вычислительных ресурсов для избыточных пересчёта элемента(ов). В следующих разделах (статьи) мы вначале представляем метод избавления от избыточных пересчётов элементов и т.о. увеличения скорости моделирования. Базовая идея – это разделить и управлять схемой в более чем одном кластере на логическом процессоре. Вместе с мультикластерным управлением повторный пересчёт после откатов ограничивает небольшие регионы без значительных расходов на управление. Во-вторых, представлен механизм динамической балансировки нагрузки. Вместо использования техники перемещения процессов, используемой в распределенных операционных системах, мы используем метод перемещения кластеров перед выполнением процесса моделирования.
Рассмотрим выполнение отката, выполняемого на ЛП для одной части схемы. Когда это происходит, целая часть схемы «откатывается» назад, т.е. все события, выполненные в этой части после времени отката отменяются и моделирование начинается c этого времени. Если сравнить результаты моделирования перед откатом и после пересчета, обнаружится, что очень часто результаты отличаются только на небольших участках части схемы (partition). Действительно много времени расходуется на пересчет большого кол-ва событий во вторую очередь, которые часто управляют на некоторые результаты моделирования. Как это можно предотвратить?

|
Рисунок 2. Множественный кластеринг |
Только элементы, которые влияют на откат, должны быть пересчитаны. Но издержки при поиске этих элементов являются значительными. Хорошее решение – деление части схемы на небольшие кластеры (100-1000 элементов на кластер). Только немногие из этих кластеров будут подвержены откату, остальная часть схемы останется неизменной. На рисунке 2 показано, что откат вызван одним событием от сигнала S и происходит с минимальной стоимостью, когда только совместные с ним элементы пересчитываются. Соединенные кластеры, откат может быть ограничен общими кластерами 2 и 3, т.е. только элементы этих кластеров должны быть пересчитаны. Стоимость выполнения отката обходится минимальной возможной стоимостью.
Новая стратегия - включение множественного кластеринга в ЛП - порождает две новые проблемы:
|
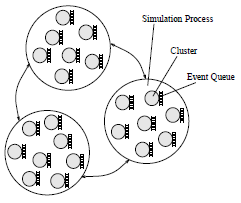
Рисунок 3. Множество кластеров на ЛП |
В системе моделирования используется механизм управления виртульным временем Джефферсона, использующий ленивую отмену и инкрементальное сохранение состояний. Очередь событий на ЛП разделяется на отдельные очереди для каждого кластера (см. рис. 3).
Используется метод Королла; идея: выделить сильно связанные регионы в схеме и соединить их в отдельном кластере, называемом «венчиком» с минимальной стоимостью разрезания.
|
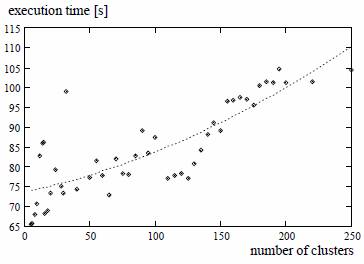
Рисунок 4. Зависимость времени выполнения от количества кластеров |
Очень часто выполнение алгоритма Time Warp на распределенной сети измеряется для совершенных условий, когда доступные ЦПУ могут быть использованы полностью (безраздельно). В таком случае баланс нагрузки при параллельном логическом моделировании может быть легко достигнут с одним подходящим разделением перед началом моделирования. Это статическое разделение может быть использовано до конца моделирования без модификации и кол-во откатов остается небольшим. В реальной среде ситуация отличается. В реальности пользователи начинают работу в произвольные моменты времени. Вычислит. мощность изменяется со временем на ЦПУ и она используется неэффективно.
Вычислительная мощность изменяется в процессе моделирования. Для оптимистического процесса общее время моделирования будет определяться самым медленным ЦПУ.
Для выполнения баланса используется 3 составляющие:
Все эти методы не позволяют получить хорошего баланса нагрузки. В первом случае, моделирование должно быть синхронизировано, остановлено и повторное разделение схемы занимает много времени. Второе решение – слишком маленькое количество рабочей загрузки изменится и будет достигнуто незначительное изменение загрузки при моделировании. Для третьего подхода вероятность зависит исключительно от ОС и не является главным переносимым решением.
Чтобы получить значительный сдвиг рабочей загрузки, 5-10% схемы должно быть перенесено на некоторый ЛП. В нашем примере – 200-400 элементов. Это может быть получено при использовании описанного мультикластерного ЛП, когда кол-во кластеров допускается перед запуском моделирования. Перемещение кластера в некоторый ЛП заключается в следующих шагах: Информация по статической топологии на кластере определяет ЛП назначения. Во-вторых, все сигналы и состояния элементов, невыполненные события и информация о последующем событии сохраняется относительно этого перемещаемого кластера. И наконец, все остальные ЛП оповещаются об изменении этого расположения. Преимущественно включение мульти-кластерных разделений остается и не влияет на переносимость кластера.
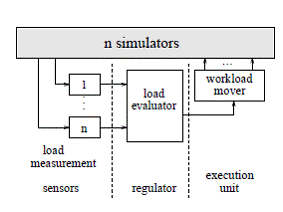
Проблема баланса нагрузки может быть решена посредством «контрольного механизма». Регулятору нужно принимать решение когда сдвигать какой кластер с какого ЛП на кокой ЛП в среде, чья загрузка при этом случайно изменится. Мы решаем эту проблему с использованием алгоритма в главном контролирующем процессе, который включает в себя три главных компонента (см. рис. 6):
|
Рисунок 6. Механизм контроля |
VTP (Virtual Time Progress) – виртуальное время продвижения – обратная мера загрузки, показывает, как быстро процесс моделирования продолжается в Вирт. времени.
Вычисление VTP.
Во-первых, вводится интегрированное VT (IVT) для одного ЛП в реальном времени ts, к-рое вычисляется на каждом шаге моделирования S для каждого кластера в этом ЛП. ∆Ts – длина шага моделирования S в единицах виртуального времени; ns – кол-во кластеров, задействованных в течение этого шага моделирования. Для IVT получим:
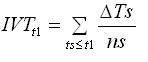 |
(1) |
Шаги, которые посчитаны дважды при откате, включаются в эту сумму. В течение интервала времени [t1;t2] VTP для одного ЛП определяется так:
 |
(2) |
Увеличение количества событий, которые выполнены в течение постоянного периода реального времени приведут к уменьшению VTP, если рабочая нагрузка не изменится. Если наоборот – количество событий неизменно, но внешняя загрузка изменяется (процессы запущены и т.д.), VTP также уменьшится. В обоих случаях баланс нагрузки должен быть рассмотрен.
Конечно, перемещение кластера нуждается в определенном времени, которым нельзя пренебречь. В течение этого времени посылка и прием ЛП не может продвинуться в Вирт. времени. Поэтому баланс нагрузки инициализируется только если отношение между соответствующими VTPs является достаточно большим.
На рисунке 7 показано, как может быть получено tBE:
 |
| Рис. 7. Время безубыточности |
Здесь trec – это время, необходимое для перемещения кластера, tBE – время балансировки. Сплошная линия – измеряет прогресс в глоб. прогрессе моделирования VT (глобальное VT) перед балансировкой нагрузки. VTPpred – это предсказанное VTP, если балансир. нагр. выполнится. VTP и VTPpred м.б. легко посчитаны с помощью глобального процесса контроля, к-рый имеет инф. об VTPs и кол-ву кластеров в каждом ЛП.
Баланс нагрузки осуществляется, если выполняется следующее условие:
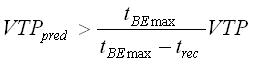 |
(3) |
Предложенный алгоритм использует максимальную точку безубыточности в качестве входа. Таким образом поведение стратегии балансировки нагрузки может быть откорректировано для конкретной среды выполнения.