Сегодня представить современное производство без каких-либо средств автоматизации очень сложно. Каждое мелкое или крупное предприятие так или иначе сталкивается с системами автоматизированного проектирования. И в частности с CAD системами.
Как правило, основой САПР является графический редактор, при помощи которого создаются и редактируются электронные макеты, состоящие из примитивов (точек, отрезков, дуг и тд). Примитивы могут быть объединены в блоки и многократно использованы при создании других электронных макетов, что колоссально повышает производительность труда инженера-проектировщика. Современные программы позволяют создавать и редактировать пространственные модели объектов практически неограниченной сложности.
Фундаментальный компонент в архитектуре системы трехмерного моделирования – геометрическое ядро. Геометрическое (математическое) ядро — это набор функций, выполнение которых обеспечивает построение трехмерных моделей. Ядро не самоценно, оно создается для использования в прикладных программах. Доступ к функциям ядра конечному пользователю открывает CAD-система (как правило, через графический пользовательский интерфейс). Кроме того, ядро иногда называют «движком» системы геометрического моделирования. Подобно тому, как двигатель автомобиля определяет «потолок» его скорости, математическое ядро определяет предел функциональных возможностей использующей его САПР.
Основные функции ядра:
- представление геометрических данных в контексте системы;
- реализация хранения данных в нейтральных форматах для обеспечения интеграции с существующими системами, необходимой для возможности широкого распространения продукта;
- реализация типичных операций представления, таких как масштабирование, поворот и перемещение поверхностей;
- реализация простейших операций редактирования тел и поверхностей;
- интерактивное взаимодействие с компонентами математической модели проектируемого изделия и получения сведений о размерах и положении частей математической модели.

Схематически ядро можно представить, как показано на рис 1.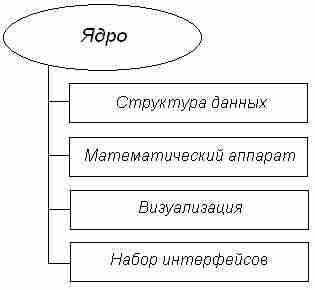


Рис 1. Структура ядра


Структура данных и топология

Топология определяет отношения между простыми геометрическими объектами, которые могут быть связаны между собой и представлять единый сложный геометрический объект. Структуры данных, используемые для описания объемных тел, обычно делятся на три типа в зависимости от того, какие тела ими описываются.

Первая структура представляет собой дерево, описывающее историю применения булевских операций к примитивам. Журнал операций носит название конструктивное представление объемной геометрии (CSG). А само дерево называется деревом CSG


Рис 2. Дерево CSG

Дерево CSG обладает следующими преимуществами [1]:
· структура данных проста, а их представление компактно, что облег-чает обработку;
· объемное тело, описываемое деревом CSG, всегда является коррект-ным, то есть его внутренний объем однозначно отделен от внешнего. Примером некорректного объемного тела является тело с лишним ребром. Для него деление объема на внутренний и внешний вблизи вершины, к которой подходит это ребро, оказывается неоднознач-ным;
· представление CSG всегда может быть преобразовано к соответст-вующему представлению B-Rep. Это позволяет взаимодействовать с программами, ориентированными на использование B-Rep;
· параметрическое моделирование легко реализуется изменением па-раметров соответствующих примитивов
Недостатки [1]:
· поскольку дерево CSG хранит историю применения булевских опе-раций, в процессе моделирования могут использоваться только они. Это требование жестко ограничивает диапазон моделируемых объек-тов. Более того, оно исключает использование удобных функций ло-кального изменения, таких как поднятие и скругление;
· для получения сведений о граничных поверхностях, их ребрах и свя-зях между этими элементами из дерева CSG требуется сложные вы-числения. К сожалению, сведения о границах нужны для множества приложений, в частности для отображения тел. Для того, чтобы ото-бразить затушеванное изображение или чертеж объемного тела, нужно иметь информацию о гранях или вершинах этого тела. Поэто-му представление CSG является недостаточным для интерактивного отображения тел и манипулирования ими. Другой пример – расчет траектории движения фрезы с ЧПУ для обработки поверхностей те-ла. Для этой задачи нужны сведения о поверхностях, их ребрах и связности. Получить все эти данные из дерева CSG очень непросто.

Из-за этих недостатков разработчики программ, основанных на представ-лении CSG, стараются добавить соответствующие сведения о границах. Такое комбинированное математическое представление называется гибридным и тре-бует поддержания согласованности между структурами данных.

Вторая структура содержит сведения о границах объема (вершинах, реб-рах, гранях) и их соединении друг с другом. Это представление называется гра-ничным представлением (boundary representation - B-rep). Многие структуры B-rep строятся по-разному в зависимости от того, какой элемент считается основ-ным при сохранении сведений о связности.
Допустим, есть тело, представленное на рис. 3.

Рис 3 Дерево CSG

В структуре B-Rep это тело будет выглядеть, как показано в табл. 1.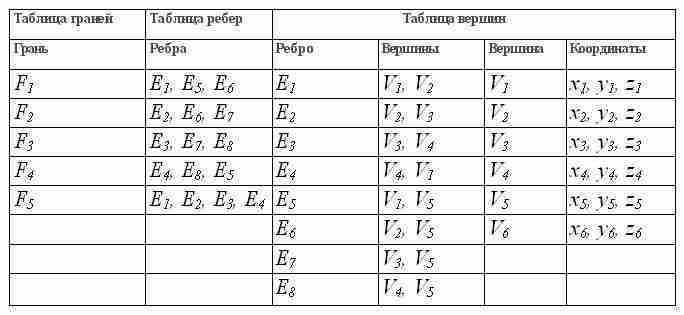



Табл 1. Представление тела в структуре B-Rep

В каждой строке таблицы ребер хранятся вершины, находящиеся на кон-цах соответствующего ребра, а в строках таблицы вершин хранятся координаты всех вершин. Эти координаты обычно определяются в модельной системе ко-ординат, связанной с данным телом. Если убрать отсюда таблицу граней, эту структуру данных можно будет использовать для хранения форм, созданных в системах каркасного моделирования. Структура данных для каркасной модели может использоваться в качестве базовой для систем автоматизированной раз-работки чертежей, если допустить указание двумерных координат для точек.
Структура данных B-Rep выглядит очень простой и компактной. Однако она не используется в развитых системах твердотельного моделирования из-за перечисленных ниже недостатков.
· Структура данных B-Rep ориентирована на хранение плоских много-гранников. Если потребуется сохранить данные о теле с криволиней-ными гранями и ребрами, то строки таблиц граней и ребер придется изменять таким образом, чтобы в них можно было включить уравне-ния поверхности и кривой соответственно (уравнения поверхностей и кривых, а также координаты вершин называют геометрическими данными, тогда как отношения между гранями, ребрами и вершина-ми называют топологическими данными. Данные в любой структуре B-Rep могут быть классифицированы либо как геометрические, либо как топологические). Уравнения для плоских граней сохранять не обязательно, поскольку плоские грани определяются находящимися на них вершинами.
· Грань с внутренними и внешними границами (рис. 4 а) не может быть сохранена в таблице граней, поскольку для нее нужно два списка ребер вместо одного. Такие грани появляются, например, при моделирова-нии объемных тел со сквозными отверстиями. Простым решением этой проблемы является добавление ребра, соединяющего внешнюю и внутреннюю границы (рис. 4 б). В этом случае два списка вершин мо-гут быть объединены. Соединительное ребро называется мостиком или перемычкой (bridge edge) и попадает в список ребер в двух экземплярах.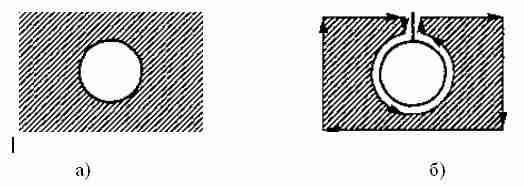

Рис. 4. Поверхность с двумя границами и метод их обхода
· Количество ребер у разных граней может быть различно (см. табл.1). Более того, невозможно определить заранее количество столбцов (по одному на каждое ребро), которые потребуются для конкретной грани, поскольку это количество может меняться в процессе моделирования. Следовательно, количество столбцов должно сохраняться в виде пере-менной в момент объявления таблицы граней. Работа с таблицей пере-менного размера создает некоторые неудобства.
· Получать сведения о связности непосредственно из данных, сохранен-ных в трех таблицах, может быть довольно утомительно. Представьте себе поиск двух граней с общим ребром в случае граничного представ-ления тела в трех таблицах. Придется просмотреть всю таблицу граней, чтобы найти строки, в которых присутствует нужное ребро. Если нужно найти все ребра, соединяющиеся в конкретной вершине, опять-таки придется просматривать всю таблицу ребер. Легко видеть, что при больших размерах таблиц поиск в них становится крайне неэффективным.

Есть две распространенные структуры данных, которые позволяют избе-жать перечисленные проблемы при сохранении граничного представления объ-емного тела. Это структура полуребер (список граней, каждой из которых со-ответствует двусвязный список ребер, главная роль отводится граням) и структура крыльевых ребер (главная роль отводится ребрам, для каждого реб-ра сохраняется список граней, которым оно принадлежит, ребер, с которыми оно имеет общие вершины, и вершин на его концах).

Третья структура представляет объем в виде комбинации элементарных объемов (например, кубов) – декомпозиционная модель (воксельное представ-ление, октантное дерево – совокупность шестигранников, ячеечное представле-ние).


Рис. 5. Декомпозиционная модель

Математический аппарат

Математический решает ряд задач. Это непосредственное представление кривых и поверхностей, пересчет координат при изменении параметров (это выполняет т.н. параметризатор), а также решение систем уравнений для нахождения пересечения поверхностей и кривых.
Для каждого криволинейного ребра в компьютере хранится либо уравнение кривой, либо эквивалентные характеристические параметры (центр, радиус, вектор нормали к плоскости, в которой лежит окружность, - примеры характеристических параметров, эквивалентных уравнению окружности).
Уравнения кривых можно разделить на два основных типа [1]. К первому типу относятся параметрические уравнения, описывающие связь координат x, y и z точки кривой с параметром. Ко второму типу относят непараметрические уравнения, связывающие x, y и z некоторой функцией.
В САПР чаще всего используются параметрические уравнения кривых и поверхностей. В некоторых случаях точки пересечения кривых удобно искать, если одна из кривых задана в параметрической форме, а другая – в непараметрической. Поэтому в отдельных системах используется преобразование уравнений из параметрической формы в непараметрическую и обратно.
Чаще всего для описания кривых, используемых в программах CAD, используются уравнения третьего порядка, потому что они обладают важным свойством: две кривые, описываемые такими уравнениями, могут быть соединены таким образом, что вторые производные в точке соединения будут равны друг другу. Это означает, что кривизна в точке соединения остается постоянной, отчего кривые кажутся одним целым. Ту же непрерывность можно получить и для кривых более высоких порядков, однако работа с ними требует интенсивных вычислений.
Уравнения поверхностей, как и уравнения кривых делятся на два основных типа: параметрические, связывающие значения x, y и z со значениями параметра (самые распространенные), и непараметрические, связывающие координаты x, y и z непосредственно друг с другом какой-либо функцией.
Расчет точек пересечения кривых необходим для определения границ ксегментов при применении булевских операций. Ксегмент - часть кривой, по которой пересекаются две грани, относящиеся к разным объемным телам. Ксегмент принадлежит обеим граням. Границы ксегмента получаются путем вычисления точек пересечения кривой, ограничивающей пересекающие поверхности, с кривой, по которой пересекаются эти поверхности (относящиеся к разным телам). После получения границ ксегмента нужно сделать еще один шаг, чтобы разделить кривую пересечения в точках пересечения.

Модуль визуализации

Раньше почти все приложения работы с графикой имели свой внутренний графический движок. Сейчас же появились специализированные графические библиотеки.
Конкретное приложение может обращаться напрямую через аппаратно-зависимый драйвер устройства или через графическую библиотеку.
1) Приложение -> драйвер -> Устройство ввода/вывода.
2) Приложение -> Графическая библиотека -> Драйвер -> Устройство ввода/вывода
Недостаток первого подхода – требуется поддержка большого количества видеокарт.
Графическая библиотека представляет собой набор подпрограмм, предназначенных для решения определенных задач. Она основывается на командах драйвера устройства. В современных САПР для визуализации используется библиотека OpenGL.

Набор интерфейсов API

API (Application Program Interface) – интерфейс прикладной программы. Набор таких интерфейсов должен обеспечить взаимосвязь между внешними модулями прикладной программы и низкоуровневыми функциями ядра, а так же между компонентами ядра – различными библиотеками.

Вместо заключения
Разработка ядра является очень наукоемкой и сложной задачей. Для её реализации требуется привлечение большого числа высококвалифицированных специалистов и, в первую очередь, математиков. Разработка и отладка функции ядра может занять очень длительный срок, что не всегда приемлемо для многих компаний.

Литература

1. Ли К. Основы САПР (CAD/CAM/CAE). – СПб.: Питер, 2004. – 560 с.