Обобщенный кодо-логический базис в вычислительном моделировании и представлении знаний: эволюция идеи и перспективы развития

Источник: Научные труды Донецкого национального технического университета. Серия "Информатика, кибернетика и вычислительная техника" (ИКВТ-2005) выпуск 93: - Донецк: ДонНТУ, 2005. C. 289-316.

Abstract

Anoprienko A. A. Generalized code-logical basis in computer simulation and knowledge representation: Evolution of idea and prospects of development. Twenty years' evolution of the concept of multidimensional code-logical basis is described, and main directions of its development in the field of logic, coding, computer simulation and organization of computer systems are analyzed.

Эволюция идеи

В статье обобщаются и развиваются исследования, впервые начатые автором в 1986 году на завершающем этапе работы над кандидатской диссертацией, посвященной повышению производительности систем генерации изображений. Проведенный при этом поиск наиболее эффективных средств и методов кодирования изображений для высокопроизводительных систем машинной графики стал источником некоторых важных идей, одна из которых, в частности, в самом общем и кратком виде была изложена в работе [1]. В этой работе было предложено обобщение метода приоритетов для повышения эффективности описания трехмерных объектов и сцен путем использования октантных полидеревьев с произвольным количеством вершин полигонально описываемых объектов и переменной разрядностью их представления в каждом вокселе, в качестве которых рассматривались листья полидеревьев. Круг идей, связанных с представлением объектов различной размерности в виде древовидных структур (двоичных, квадрантных, октантных и др.) стал одним из основных источников концепции многомерного кодо-логического базиса. Материалы исследований в данном направлении частично вошли в кандидатскую диссертацию автора [2], частично – реализованы в виде технических решений, новизна которых подтверждена целым рядом авторских свидетельств на изобретения (см., например, [3, 4]).

Другим источником концепции стал поиск компьютерных аналогов генетического кодирования. Благодаря стечению обстоятельств, хронология и непосредственные причины формирования идей данного направления зафиксированы автором с предельной точностью. В порядке объяснения авторской мотивации в контексте исследований многомерного кодо-логического уместно привести некоторые детали этих событий. Непосредственно после успешной защиты кандидатской диссертации (октябрь 1987 года) естественным образом возник вопрос о наиболее эффективных вариантах дальнейшего продолжения диссертационных исследований. Определяющим моментом можно считать прочтение книги Н.Н.Моисеева «Алгоритмы развития», где обращалось особое внимание на феномен генетического кода, который, будучи единым для всего живого, строится на базе всего 4-х символов, обеспечивающих не просто сохранение и передачу чрезвычайно объемной наследственной информации [5, c. 15], но и непрерывную эволюцию органической материи в процессе ее усложнения и самоорганизации. При этом утверждалось, что «единый мировой процесс развития – это не просто игра случая, а непрерывное усложнение организации, происходящее в результате взаимодействия объективной необходимости со столь же объективной стохастичностью нашей Вселенной. Реальность такова, что необходимость вовсе не исключает случайность, но определяет потенциальные возможности развития… » [5, c. 19]. Размышления о том, как переход от бинарного кодирования к представлению информации на базе неких 4-х символов мог бы привести к качественно новым свойствам компьютерной памяти, привели в конечном итоге к выводу о том, что наиболее естественным решением является дополнение традиционных двоичных значений 0 и 1 состояниями их равновероятности и одновременности. Другими словами, не только НЕ (отрицание), но также и логические операции ИЛИ и И должны быть реализованы уже на уровне элементарного кодирования логических состояний. Эти мысли практически сразу же оформились в своеобразную предварительную программу исследований, одним из узловых пунктов которой явилась проверка гипотезы о целесообразности многомерного подхода к представлению не только логического пространства, но и количественных значений на числовой оси. Т.е. фактически был поставлен вопрос разработке нового способа численного кодирования, позволяющего в полной мере использовать преимущества новой логики.

В последующем в результате анализа того, что уже было известно о генетических кодах, выявилось настолько много параллелей с идеей нового способа кодирования, что было принято решение отказаться от первоначального его обозначения как «квадрантного» (по аналогии с кодированием двумерных изображений) в пользу определения «квазигенетическое». И уже тогда в качестве основной области применения новых подходов представлялось именно компьютерное моделирование. Сформировалось такое убеждение во многом также благодаря идеям Н.Н. Моисеева, который, в частности, рассматривал модель в первую очередь как своеобразное «упакованное» знание, представляющее собой специфическую форму наиболее эффективного кодирования разнородной информации. При этом, в отличие от обычных способов кодирования, модель за счет специальной систематизации имеющейся информации может нести в себе кроме уже известного и потенциальное знание, выявляемое в последующем в процессе работы с моделью [5, с. 166].

К сожалению, в силу разных обстоятельств, реально продолжить эти исследования удалось лишь в марте 1992 года, непосредственным поводом для чего явилась подготовка предложений в программу исследований образованной тогда Украинской академии информатизации. Предполагалось также, что данная тема может стать основой диссертационного исследования ассистента кафедры ЭВМ ДонНТУ (тогда еще ДПИ) Кухтина А.А., принимавшего в то время участие в целом ряде совместных с автором проектов. Основным результатом данного периода стал сделанный в Киеве в ноябре 1992 года доклад «О некоторых возможностях расширения логического базиса информатики» [6], в котором впервые была официально сформулирована и проанализирована концепция двумерного логического пространства в варианте, ставшем в последующем основой многомерного кодо-логического базиса.

С 1994 года продвижение в развитии идеи многомерного кодо-логического базиса стало более систематичным благодаря началу работы автора над докторской диссертацией в рамках докторантуры под руководством профессора В.А. Святного. Важным этапом при этом стала стажировка в Институте параллельных и распределенных суперЭВМ (Штуттгартский университет, Германия) под руководством профессора А. Ройтера с октября 1994 г. по февраль 1995 года. В докладе, сделанном по результатам стажировки на институтском семинаре 31 января 1995 год были, в частности (в числе прочих вопросов), рассмотрены и перспективы развития «квазигенетической» логики и «квазигенетического» кодирования. При этом было предложено ввести в рассмотрение кроме традиционных логических и арифметических операций специальные «генетические» операции, предполагающие генерацию конкретных «точечных» значений на основе «квазигенетических» кодов, а также – разного рода их модификации или «мутации».

В 1996 году в рассмотрение вводятся понятия «тетралогика» и «тетракоды» [7], альтернативные определению «квазигенетические», что в последующем позволило обобщить данный подход как на кодо-логический базис, предшествующий бинарному («монологика» и «монокоды»), так и на базисы более высокого порядка, чем четверичные [8]. Особо следует отметить, что в работе [7] кроме двумерного логического пространства были также рассмотрены и двумерные интерпретации тетракодов. Параллельно в этот период исследовались и вопросы возможного использования тетракодов для кодирования изображений [9, 10], а также – использование методов стохастической геометрии для анализа и синтеза вычислительных систем и алгоритмов нового поколения [11]. Кроме того, в контексте поиска средств и методов повышения эффективности вычислительного моделирования особое внимание уделялось развитию концепции универсальных моделирующих сред, ориентированных на сетевую (распределенную и/или параллельную) вычислительную инфраструктуру [12-14], что явилось, по сути, первым шагом к концепции расширенного алгоритмического базиса [15].

Важнейшим моментом при этом стало формулирование идеи о множественности эволюционирующих кодо-логических форм качественного и количественного представления знаний [8]. При этом утверждалось, что «человеческий интеллект в зависимости от конкретной ситуации и решаемой задачи использует в процессе мышления не одну логическую систему, а некоторое достаточно представительное множество таких систем и связанных с ними количественных представлений. Традиционно используемая двоичная логика и основанные на ней системы счисления должны рассматриваться при этом в качестве одного из наиболее значимых, но отнюдь не единственных и не достаточных элементов современного интеллектуального инструментария. Другими важными составляющими являются как некоторые более ранние формы мышления и представления количественной информации, так и целый ряд перспективных, которые существуют пока только в зачаточном или не полностью оформившемся виде, но обладают значительным информационным потенциалом» [8, c. 59].

В 1997 году некоторые результаты исследований по многомерному кодо-логическому базису были впервые представлены в англоязычном информационном пространстве. В первую очередь речь идет о докладах на международной конференции по моделированию в Стамбуле [16, 17] и международном конгрессе по научным вычислениям, моделированию и прикладной математике в Берлине [18].

В 1999-2001 гг. удалось существенно продвинуться в исследовании и понимании феномена монокодов и монокодовых вычислительных моделей [20-23]. Это позволило не только понять многие закономерности эволюционного развития методов и средств кодирования количественной информации, в т.ч. ее интеграции в комплексные вычислительные модели, но и впервые предложить достаточно обоснованные решения и интерпретации для некоторых достаточно известных трудноразрешимых научных проблем, среди которых в первую очередь можно назвать проблему Фестского диска [20].

В 2002 году возможности практического применения тетралогики была продемонстрирована путем разработки специальной методики модельной и компьютерной поддержки принятия решений в ситуациях когнитивного конфликта [24]. Применение предложенной методики и специальных средств ее реализации для всестороннего анализа одной из типичных научных проблем, характеризующихся обилием противоречивой и малодостоверной информации, позволило показать специфику и преимущества именно новых подходов к решению такого рода задач.

В 2002-2003 году были также получены существенные результаты в разработке нового поколения распределенных моделирующих сред [25-29], являющихся по сути одной из важнейших областей эффективного применения расширенного кодо-логического базиса, который в данном случае должен рассматриваться в неразрывной связи с расширенным алгоритмическим базисом.

В данной публикации обобщаются ранее полученные результаты исследований по многомерному кодо-логическую базису и излагаются некоторые новые идеи исследований и разработок в данном направлении.

Переломный 1994-й

В 2000 году в большой обзорной работе «Логика на рубеже тысячелетий» А.С. Карпенко пришел к весьма характерному выводу, суть которого в следующей цитате: «Приходится констатировать, что конец века и конец второго тысячелетия, а именно 1994 г. стал той критической точкой, когда под неимоверным давлением окончательно рухнула конструкция под названием “классическая логика”» [30]. Свой тезис А.С. Карпенко аргументировал, в частности, следующим фактами: в этом году в Англии и США издается большой сборник работ под названием “Что есть логическая система?” [31]. В этом же году практически с таким же названием публикуется философская работа логика с мировым именем Хао Вана [32], которая открывается определениями логики, начиная от Канта и вплоть до Гёделя, и заканчивается характеристикой логики, данной Л. Витгенштейном в 1921 г.: “Логика трактует каждую возможность, и все возможности суть её факты”. И в этом же году под названием “Что есть истинная элементарная логика?” появляется статья выдающегося логика и философа Яакко Хинтикки [33], в которой развивается новая концепция IF-логики (Independence Friendly - дружественной к независимости). В это же время выходит целый ряд статей, связанных с развитием и применением альтернативных (неклассических) логик. В частности, с 1994 года начала публиковаться целая серия работ Д. Батенса и его учеников, где разработана логика, способная моделировать рассуждения, в ходе которых смысл логических терминов может измениться. В итоге возникло новое направление исследований, названное “адаптивными логиками” [34].

В итоге А.С. Карпенко детализирует содержание «революции 90-х» в логике как фактическое исчерпание к этому времени практического потенциала ее простейших форм: «Необычайный прогресс в хранении и, главное, в обработке информации на основе булевой (классической) логики имеет не только свои естественные физические пределы. Homo-логический универсум не является счётным, а процессы, в нем происходящие, не являются истинностно-функциональными. Всё, что можно извлечь из предельного огрубления человеческой логики, впервые представленного работами Шеннона, Шестакова и Накасимы (а это было не что иное, как одна из конкретизаций булевого универсума), как раз извлекает происходящая сейчас компьютерная революция. Но в конечном итоге эта конкретизация тупиковая для создания искусственного интеллекта хоть мало-мальски соответствующего человеческому. Обозначилась явная тенденция к разработке новой логики, которая по своим выразительным средствам намного богаче классической. Этим объясняется пристальное внимание специалистов к многозначным (бесконечнозначным) и нечеткозначным логикам (которые континуальны) в работах по искусственному интеллекту и в других работах» [30].

Но главный смысл наметившихся в 1994 году изменений А.С. Карпенко совершенно справедливо увязал с текущим уровнем развития компьютерных технологий и соответствующим смещением акцентов в развитии логики в направлении получения максимального практического результата: «Тематика абстрактной логики и общетеоретические проблемы обоснования математики… отступают перед новыми тенденциями в развитии логики конца ХХ века. Логика становится всё более насущной в компьютерных науках, искусственном интеллекте и программировании. Подобное приложение логики порождает большое число новых логических систем, но уже нацеленных непосредственно на их практическое применение» [30]. И действительно, именно к 1994 году в качестве самостоятельного научного направления оформилась новая комплексная дисциплина, получившая в последующем обобщенное название “вычислительный интеллект” (ВИ), и которая по мнению многих специалистов, в т.ч. основоположника теории нечетких множеств Л. Заде, должна была стать наиболее перспективной альтернативой т.н. «искусственному интеллекту» (ИИ). Одной из основных особенностей ВИ явилась ее ориентация на “мягкие вычисления” (“Soft Computing”), концептуально описанные Л. Заде вместе с понятием ВИ именно в 1994 г. [35]. Фактически это означало качественно новый этап и в развитии идей нечеткой логики, получивших к 94-му году как бы «второе дыхание», что выразилось в появлении многочисленных аппаратных и программных реализаций, использующих соответствующие подходы.

Концепция “вычислительного интеллекта” в настоящее время положена в основу создания нового поколения вычислительной техники, в качестве одного из основных названий которого используется определение Real World Computers (RWС) – “компьютеры реального мира”, что призвано подчеркнуть максимальное приближение новых компьютерных технологий к реально используемым человеком и живой природой средствам и методам кодирования, обработки, преобразования и передачи информации. В работе [8] в связи с этим отмечалось, в частности, что в качестве одной из важнейших составляющих “вычислительного интеллекта” является компьютерное моделирование, эффективно использующее весь спектр интеллектуализации вычислительных методов и средств. А в качестве соответствующего направления исследований была предложена концепция расширенного кодо-логического базиса, предназначенная, во-первых, для обобщения и систематизации уже имеющихся в этой области результатов, а во-вторых – для обеспечения возможности синтеза нового поколения средств и методов моделирования.

Ко всему сказанному следует также добавить, что 1994-й год стал во многом переломных и в развитии самих компьютерных технологий. Главным при этом был глубинный переход от преобладания классической фон-неймановской последовательной парадигмы организации вычислительных процессов к тотальному параллелизму на всех уровнях организации вычислительных структур. Проявилось это, в частности, в следующем:

Во первых, в 1994 года фирма Intel заканчивает разработку процессоров нового поколения, получивших обозначение Pentium и имеющих суперскалярную архитектуру, позволяющую выполнять за такт более чем одну инструкцию. В этом же году фирма NexGen на базе производственных площадей IBM начинает выпускать процессор Nx586 с аналогичной архитектурой, который через несколько лет после приобретения NexGen фирмой AMD станет основой для создания основных конкурентов Pentium, а именно процессоров K6, Athlon и последующих [37]. Фактически это означало практически всеобщий переход с 1994 года на суперскалярную параллельную архитектуру, начиная с уровня однокристальных процессоров.
Во-вторых, в июне 1994 года Intel и HP заключили соглашение о сотрудничестве в области разработки нового поколения 64-разрядных микропроцессоров, на которых приложения для платформы x86 и для Unix-систем работали бы одинаково хорошо. Разрабатываемая архитектура IA-64 предполагала, в числе прочего, обязательную реализацию параллелизма начиная уже с уровня объединения нескольких инструкций в одной команде (Ecplisity Parallel Instruction computing – EPIC). А параллелелизм на всех уровнях признавался магистральным направлением дальнейшего развития компьютерных технологий [38].
В-третьих, летом 1994 года в научно-космическом центре NASA – Goddard Space Flight Center (GSFCJ), а точнее в созданном на его основе центре CESDI5 (Center of Excellence in Space Data and Information Sciences) был реализован проект Beowulf (www.beowulf.org), название которого превратилось в имя нарицательное для всех последующих кластерных систем такого рода (Beowulf-кластеры). Первоначальный кластер, который и был назван "Beowulf", создавался как вычислительный ресурс проекта Earth and Space Sciences Project (ESS) и состоял из 16-ти узлов на обычных процессорах 486DX4/100MHz с 16MB памяти и 3-мя сетевыми адаптерами на каждом узле, обеспечивающими связь через 3 обычных Ethernet-кабеля. Основное значение данного проекта заключалось в том, что впервые была наглядно продемонстрирована возможность достижения сверхвысоких показателей производительности на базе кластера, использующего самые обычные компьютерные компоненты массового производства. А это фактически означало начало массового применения параллельных вычислений и на сетевом уровне [39].
В четвертых, с июня 1993 года в университете Мангейма (Mannheim, Германия) совместно с лабораторией Netlib (США) началось ежегодное формирование списка 500-т наиболее производительных вычислительных систем в мире. Уже в 1994-м году изменения в этом списке наглядно показали резкое сокращение числа однопроцессорных систем в пользу систем с массовым параллелелизмом, а затем – и кластерных систем.
В-пятых, к 1994 году Интернет окончательно превратился в глобальную Сеть, стимулом к лавинообразному росту которой стало утверждение к 94-году стандартов на язык гипертекстовой разметки HTML (версия 2.0) и сопутствующие технологии, на базе чего сформировалось, то, что получило наименование WWW – World Wide Web («Всемирная паутина»). Знаковым явлением при этом можно считать образование в 1994-м году первой компании, ошеломляющий коммерческий успех которой целиком и полностью был основан на существовании Сети. Этой компанией явилась Netscape Communication, основанная разработчиками первого в мире браузера Mosaic и бывшим профессором Стенфордского университета Джимом Кларком, ранее основавшего компанию Silicon Graphics, ставшую одним из лидеров в разработке высокопроизводительных вычислительных систем. Начав с выпуска в 1994 браузера Netscape Navigator, компания в 90-е годы стала одной из наиболее успешных компьютерных корпораций благодаря своему вкладу в развитие клиентских и серверных web-технологий, позволивших в кратчайшие сроки добиться действительно массового использования Сети и превращения ее по сути в единую сверхпроизводительную информационно-вычислительную среду [40, с. 106].
В-шестых, в 1994-м году закончился многолетний судебный процесс по иску ATT к университету Беркли, касающийся прав собственности на операционную систему UNIX. Судебное решение о возможности свободного распространения данной системы (наряду с существованием права частной собственности на отдельные ее версии) фактически открыло дорогу повсеместному использованию современных многозадачных операционных систем с массовым параллелелизмом процессов, основанном как на эффективном использовании квантования времени, так и на использовании множества процессоров [41, c. 62]. Итогом этого стало и массовое распространение операционных систем семейства Linux (аналогов UNIX, порожденных «Сетью и для Сети»), и переход на использование UNIX в абсолютном большинстве высокопроизводительных систем, представленных в списке Top500. Частично отражением этих процессов стал и ускоренный переход на аналогичные по своей организации операционные системы в фирме Микрософт, что в 1995 году выразилось в выпуске Windows95, а в последующем – Windows XP, что фактически означало тотальный переход на многозадачность и параллелелизм на уровне операционных систем.
В-седьмых, в 1994-м году закончилась разработка Интерфейса Передачи Сообщений MPI, ставшего первым стандартом передачи сообщений в сетевых и параллельных вычислительных средах [42, c.111]. Этим, фактически, открывалась возможность массовой реализации параллельных приложений в гетерогенных сетевых вычислительных средах, в том числе работающих на базе различных программных платформ.
В-восьмых, с 1994-го фирма SUN начинает адаптировать свою технологию платформенно независимого программирования Oak к среде Интернет, что приводит в 1995-м году к появлению технологии Java, не только обеспечившей на базе реализации принципа виртуальной машины независимость от аппаратной и программной платформы, но создавшей условия для массового перехода от последовательного программирования в среде локального компьютера к параллельному программированию множества процессов в условиях гетерогенной Сети.
В-девятых, в 1994-м году началась третья волна клиент-серверных приложений, которая в отличие от первой волны, ориентированной на файловые серверы, и второй, ориентированной на сервера баз данных, впервые в качестве основной среды реализации предполагала распределенные объекты в Сети. Основной формой реализации такой инфраструктуры распределенных объектов стала архитектура CORBA [43, с. 53].
Таким образом, в 90-е годы (кульминацией перемен можно считать 1994-й год) произошли качественные изменения как в развитии логических основ, так и в области компьютерных технологий, которые обусловили актуальность соответствующих изменений как в кодо-логическом [8], так и в алгоритмическом [15] базисе современных компьютерных технологий.

Суть данных изменений может быть сведена к переходу от преобладания фиксированной точечной определенности в логических, арифметических и алгоритмических основах функционирования компьютерных систем к эволюционирующей множественности и неопределенности.

В данной статье в развитие идей, предложенных в работах [1-29], впервые рассматриваются некоторые новые перспективы использования многомерного кодо-логического базиса в вычислительном моделировании и представлении знаний. При этом анализируются следующие 5 направлений, ориентированные в первую очередь на практическое развитие возможностей компьютерного моделирования и представления знаний:
- развитие многомерного логического пространства;
- развитие понятия числа в контексте многомерного логического пространства;
- развитие интерфейсных средств в контексте развития кодо-логического базиса;
- эволюция алгоритмического базиса на основе развития кодо-логических средств;
- переход от господства алгоритмического подхода к преобладанию различных форм модельного представления.

Многомерное логическое пространство

Рассмотренное в работах [6-8] двумерное логическое пространство может быть продуктивно расширено до трехмерного путем введения третьего измерения, соответствующего возможной недостоверности и/или «вариабельности» (т.е. возможной изменчивости) логических значений двумерного пространства (Рис.1). Традиционные логические системы являются по сути одномерными, так как строятся в пределах оси, соединяющей логические 0 и 1. В простейшем случае классической бинарной логики используются только два противоположных логических значения. В наиболее сложных случаях, при построении непрерывных, в том числе нечетких, логик используется все пространство оси 0-1.

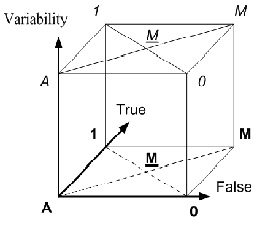
Трехмерное логическое пространство может быть порождено базисом, состоящим из ортонормированной системы векторов «Истина» (может обозначаться как Т – «True» или Y – «Yes»), «Ложь» (F – «False» или N – «No») и «Вариабельность» (V – «Variability»). Логические значения при этом могут задаваться либо соответствующими координатами (например, в случае построения непрерывных логик), либо фиксацией характерных точек. В качестве последних, прежде всего, должны быть выделены следующие:
1 и 0 – значения «истина» и «ложь» классической логики;
А – абсолютная неопределенность, «непроявленность», неизвестность;
М – фиксированная множественность, многозначность («истина» и «ложь» одновременно);
М – фиксированная равновероятность значений «истина» и «ложь», которая может рассматриваться в качестве технически реализуемого аналога состояния А.
В дополнение к этим значениям, ранее рассмотренным в работе [8], в трехмерном логическом пространстве дополнительно вводятся соответствующие значения 1, 0, А, М и М, модифицируемые при определенном условиях. Интерпретация такой модифицируемости может быть различная: например, адаптивность логики в смысле Д. Батенса [34] или допустимость ценностных изменений в логических значениях в контексте возможной смены или дополнения парадигмы «знания+аргументация» более гибкой парадигмой «знания+оправдания» [44, с.154].
В качестве одного из наиболее перспективных вариантов реализации логических систем в трехмерном базисе можно рассматривать октологику, которая в соответствии с введенной в работе [8] системой обозначений может быть описана как следующий кортеж значений: LV8= {0, 1, М, М, 0, 1, М, М }.
При этом к модифицируемым логическим значениям кроме простейших логических операций сведения всех значений только к одному из них (таблица 1), могут быть также применимы специальные одноместные модифицирующие операции (таблица 2).
Таблица 1.
Специальные одноместные модифицирующие операции

Исходные значения	Абсолютная минимизация	Абсолютная максимизация	Абсолютное распаралле-ливание	Абсолютная стохасти-зация
0	0	1	М	М
1	0	1	М	М
М	0	1	М	М
М	0	1	М	М

Таблица 2
Специальные одноместные модифицирующие операции

Исходные значения	Классическая инверсия	Операции с множественностью
		Инверсия	Максимизация	Минимизация
0	1	0	0	0
1	0	1	1	1
М	М	М	М	М
М	М	М	М	М

Аналогично одноместным операциям могут быть заданы и двуместные операции, которые будут одинаковыми как для модифицируемых, так и для фиксированных значений (табл. 3).

Таблица 3
Двуместные операции октологики

Операнд 1	Операнд 2	И (min)	ИЛИ (max)
0	0	0	0
0	1	0	1
0	M	0	M
0	M	0	M
1	1	1	1
1	M	1	M
1	M	M	1
M	M	M	M
M	M	M	M
M	M	M	M

В качестве простейших частных случаев использования вариабельности могут рассматриваться тетралогика LV4= {0, 1, 0, 1 } и дилогика LV2= {0, 1}, позволяющие реализовать свойство адаптивности в рамках подходов, характерных для традиционной бинарной логики.

Следует, однако, отметить, что определение «квазигенетическая» в наибольшей степени применимо именно к рассмотренному выше варианту октологики, т.к. именно на ее базе могут быть наиболее полно промоделированы свойства генетического кодирования, в том числе необходимые в специфических ситуациях и допустимые в определенном диапазоне мутации.

 

Развитие понятия числа

Аналогично тому, как бинарная логика является основой двоичной системы счисления, на базе рассмотренных логических систем могут быть построены соответствующие системы кодирования количественной информации. При этом в рассмотрение могут быть введены вариабельные (модифицируемые) тетракоды (CV4= {1, 0, 1, 0}) и октокоды: CV8= {0, 1, М, М, 0, 1, М, М }, функциональные возможности которых по отражению количественных соотношений и закономерностей реального мира существенно превышают возможности классической двоичной (бинарной) системы.

Двоичная логика и фиксированные системы счисления, сводимые к двоичной, – это характерные черты так называемой Неймановской архитектуры, получившей всеобщее распространение после опубликования в 1946 году отчета с участием Дж. Фон Неймана о проекте первой вычислительной машины с хранимой в памяти программой [45, c. 234]. Однако в условиях сетевой параллельной и распределенной инфраструктуры стали очевидны недостатки и ограничения классического кодо-логического базиса, частично компенсируемые алгоритмически-программным способом. Но, как известно, программная реализация функциональных возможностей, хотя и обеспечивает беспрецедентную универсальность современной компьютерной техники, тем не менее, ведет к почти неизбежному снижению производительности на 1-2 порядка по сравнению с аппаратной поддержкой соответствующих функций. А последнее может быть оправдано и целесообразно лишь при переходе к качественно новому кодо-логическому базису.

При этом неизбежным является развитие и самого понятия числа. Несколько упрощая общую схему развития в контексте обобщенного кодо-логического можно утверждать следующее:

- Монокодам соответствуют различные модификации непозиционных систем счисления, в которых различное расположение счетных знаков могло нести не весовую нагрузку, а разного рода семантическую и интерфейсную, что детально рассмотрено в работе [21].

- Дикодам, т.е. современному этапу развития, соответствуют преимущественно позиционные системы счисления, позволяющие достаточно компактно представлять практически любые «точечные» количественные значения и осуществлять алгоритмические манипуляции с ними.
- Гиперкодам, в т.ч. тетракодам, соответствуют сверхпозиционные или гиперпозиционные системы счисления, в которых «точечное» представление количественных значений может рассматриваться лишь как частный случай. В общем случае в гиперпозиционной системе число представляет из себя некоторое множество количественных значений, мощность которого и структура определяется конкретными значениями в соответствующих разрядах, т.е. на соответствующих позициях кодового представления числа. 

В традиционной математике эволюция понятия числа также может быть привязана к различным этапам развития обобщенного кодо-логического базиса:

Натуральные числа явились прямым следствием перехода от непозиционных монокодов вначале к частично позиционным системам (например, римская нумерация), а затем и к полностью позиционным системам счисления. Характерной переходной формой от монокодов к дикодам в виде натуральных чисел являются так называемые фигурные числа Пифагора [46, с.63-64]. Уходящие в седую древность истоки такой формы представления чисел хорошо характеризует высказывание известного математика XIX века Леопольда Кронекера: «Бог создал натуральные числа, все прочее – творение человека» [47, с. 24].

  Рациональные числа явились одним из наиболее существенных шагов на пути «характерного  для математики принципа обобщения. Переход путем обобщения от натуральных чисел к рациональным удовлетворяет одновременно и теоретической потребности в снятии ограничений, которые наложены на вычитание и деление, и вместе с тем – практической потребности в числах, пригодных для фиксации результатов измерений» [47, с.81]. Другими словами, естественный переход к наглядному представлению натуральных чисел, представленных в виде позиционных кодов, на числовой оси, которую в ее положительной части можно считать специфической переходной формой монокодового представления, неизбежно привел к экстраполяции оси в отрицательную область и фиксации в качестве одного из равноправных чисел нулевого значения.

Действительные числа явились прямым и естественным следствием перехода от дискретного представления числовой оси, что можно считать рудиментом монокода, к непрерывной оси, что позволило решить проблему иррациональных чисел и означало окончательный переход к дикодам, позволяющий максимально использовать все преимущества новой формы представления чисел.

Комплексные числа явились, по сути, первым следствием необходимости расширения понятия числа за пределы точечного представления на континууме действительных чисел, вызванным, однако, исключительно внутренними потребностями алгебры дикодов. В году У. Р. Гамильтоном вводятся кватернио?ны как частный случай гиперкомплексныхчисел. Кватернионы как составные числа оказались достаточно удобными для описания изометрий трёхмерного и четырёхмерного Евклидовых пространств и поэтому получили широкое распространение в механике. 

Алгебраические и трансцендентные числа явились наиболее значимым в XIX веке обобщением понятий соответственно рациональных и действительных чисел [46, c.131], впервые позволившим выйти за пределы точечного представления и ввести элементы множественности числового представления, характерные для гиперкодов. Правда, это нововведение реализовывалось лишь алгебраическим путем, не затрагивающим, фактически, кодо-логический базис. Дальнейшим развитием идей данного направления явилось формирование теории числовых полей [46, c.145-163], которую в совокупности с интенсивно развивавшейся на протяжении всего XX века теорией множеств можно считать основой перехода к  гиперкодам в XXI веке.

Гиперкоды, включая такие частные случаи как тетракоды, обеспечивающие множественность и вероятностность числовых значений, а также октокоды, позволяющие дополнительно ввести свойство случайной или контекстно-зависимой модифицируемости тетракодовых значений, можно считать новым этапе в развитии понятия числа. Однако, в данном случае переход к новому этапу обусловлен не алгебраическими потребностями, а сугубо компьютерными, в том числе связанными с потребностями компьютерного представления параметров разного рода сложных систем и процессов.
 В этой связи следует отметить, что для теоретического анализа обобщенного кодо-логического базиса в целом наиболее продуктивным представляется именно теоретико-множественный подход. При этом монокоды могут рассматриваться в качестве простейшей алгебраической системы (модели), представленной полугруппой, обладающей только свойством ассоциативности. Такая полугруппа традиционно представляется моноидом [48, c. 142], т.е. полугруппой с единицей [49, c. 58]. Все более сложные варианты дикодов и гиперкодов могут рассматриваться как различные варианты полугрупп, групп, колец и полей.

Усложнение структуры числа происходило параллельно по 2-м направлениям: кроме уже рассмотренного «алгебраического» усложнения, итогом которого стали комплексные и гиперкомплексные числа, важным фактором стало «вычислительное» усложнение, предполагавшее масштабирование значений с целью обеспечения максимальной компактности для представления максимально широкого диапазона значений. Истоком такого усложнения можно считать взвешенные монокоды, примером чего является, в частности, древнеегипетская система счисления [21]. Но наиболее эффективно масштабирование реализовывалось на базе дикодов путем представления значений в виде мантиссы и порядка, что в вычислительной технике нашло свое выражение в специальном формате с т.н. «плавающей запятой».

Неявное использование плавающей запятой появилось практически одновременно с использованием самых ранних прототипов позиционных систем счисления. Началом систематического использования плавающей запятой при вычислениях принято считать изобретение логарифмов в 1600 году и логарифмической линейки в 1630 году [45, c. 260]. Конрад Цузе уже в 1936 году в своем первом варианте вычислительной машины использовал двоичное представление с плавающей точкой, которое он назвал полулогарифмической нотацией [45, c. 260]. Наиболее революционным изменением в аппаратной реализации арифметики с плавающей запятой считается принятие в конце 80-х годов соответствующего стандарта ANSI/IEEE [45, c. 262], что стимулировало практически повсеместный переход на аппаратную реализацию вычислений с плавающей запятой в современных процессорах.

Однако, проблемы точности представления чисел в форматах с плавающей запятой породили еще в 60-е годы многочисленные исследования в области интервальной арифметики [45, c. 279], актуальность которой во многих приложений, например, в моделировании сложных динамических систем,  только повысилась за последние годы (см., например, [50]). Но на базе традиционной двоичной вычислительной техники возможна лишь алгоритмическая реализация таких подходов, что резко снижает производительность соответствующих вычислений и, следовательно, ограничивает их применение. Тетракоды и рассмотренные выше октокоды позволяют перенести интервальные вычисления на уровень реализации элементарных операций и в связи с этим  представляются наиболее перспективным направлением развития интервальных подходов в современных компьютерных вычислениях, позволяющим на определенном этапе перейти на аппаратную реализацию соответствующих процессоров.

Наиболее универсальной формой компьютерного представления тетракодов и октокодов является формат с плавающей запятой, в котором представленные соответствующим образом мантисса и порядок должны быть дополнены значениями смещений, представленных обычными бинарными кодами, обеспечивающими совместимость с традиционными двоичными операциями машинной арифметики. Другими словами, если обычные натуральные числа представляются в компьютерных системах в формате m*2e , где m – мантисса, e – порядок, кодируемые традиционно в виде дикодов (в частности, бинарных кодов), то для универсального представления тетракодов и октокодов целесообразен формат (d+m’)*2(k+e’) , где m’ – мантисса и e’ – порядок, представленные соответственно в виде целочисленных тетракодов или октокодов, а d и k – смещения, представленные в виде классического бинарного кода. При этом смещения, позволяя, с одной стороны, достаточно просто решить проблему совместимости гиперкодового представления с традиционной машинной арифметикой, с другой стороны, открывают возможности для дальнейшего усложнения структуры и многофункциональности численного представления путем введения элементов гиперкодового кодирования в представление смещений.

Развитие интерфейса

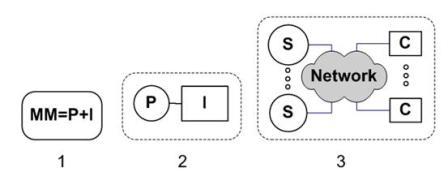
Важно также отметить, что развитие кодо-логического базиса непосредственно влияет и на эволюцию интерфейсных средств, что в первую очередь наиболее наглядно проявляется в системах вычислительного моделирования. На рисунке 2 схематически представлено развитие интерфейсной компоненты в системах вычислительного моделирования в процессе эволюции кодо-логического базиса.

 

 

При этом следует отметить, что в монокодовых моделях интерфейсные функции выполняют непосредственно размещение, форма и варианты группировки монокодовых счетных элементов. Одним из наиболее наглядных примеров этого являются Мальтинская пластина [21] и Фестский диск [20]. Именно  наглядность ранних монокодовых моделей и интегрированность в них вычислительных и интерфейсных компонент можно считать наиболее ранними и естественными проявлениями того, что в последующем было обозначено как интегрированные моделирующие среды [13, 14], обеспечивающие в числе прочего базовые функции когнитивного вычислительного моделирования [20].

Абстрагирование от количественных значений счетных элементов в дикодовом представлении чисел привело к существенной утрате наглядности и вообще к вырождению интерфейсных функций численного представления. В связи с этим интерфейсные компоненты стали приобретать самостоятельное значение в качестве средств повышения наглядности как в случае управления вычислительным процессом, так и при визуализации результатов и текущих значений. Характерным примером является организация современных операционных систем, в большинстве которых имеет место четкое разделение между основной частью системы и интерфейсом пользователя, который во многих случаях является опциональной частью, как, например, это имеет место в операционных системах семейства Линукс. Графическое представление численных дикодовых значений, хранимых в базе данных или  полученных в ходе вычислений или моделирования, в большинстве случаев (например, при использовании столбиковых диаграмм) представляет из себя по сути перевод представления значений из дикодовой формы в монокодовую как наиболее наглядную для человеческого восприятия.
Переход к сетевой парадигме вычислений еще дальше отделяет интерфейсную часть от вычислительной. При этом последняя сосредотачивается преимущественно в серверах – специальных компьютерах, все чаще  лишенных каких-либо интерфейсных средств кроме сетевого подключения. Еще одним характерным моментом сетевой парадигмы является переход от взаимнооднозначного соответствия между вычислительной частью и интерфейсной к реализации разного рода множественных соотношений, когда на базе сетевой среды может устанавливаться взаимосвязь между произвольным числом серверных и клиентских компонент (схема 3 на рис. 2). Указанная множественность в контексте перехода к гиперкодовому базису представляется вполне естественной и неизбежной.

Эволюция алгоритмического базиса

В работе [15] впервые была рассмотрена эволюция алгоритмического базиса в контексте развития обобщенного кодо-логического базиса. При этом акцент был сделан на том, что объективно необходимость такой эволюции обусловлена сложностью процессов реального мира. В современных условиях можно констатировать переход от классических последовательных алгоритмов, допускающих лишь простые формы распараллеливания, к гипералгоритмам, основанным на гиперлогике и гиперкодах.  Характерным свойствами данной категории алгоритмов являются множественная и сложная структура различных форм распараллеливания процессов, а также множественная стохастичность структуры и динамики вычислительных процессов.
Множественность в современной компьютерной инфраструктуре реализуется в основном по следующим 3-м направлениям:

1. Распараллеливание с целью повышения производительности.  Отсчет данного направления можно вести с конца 60-х или начала  70-х годов прошлого века, а точнее с системы Иллиак-4, введенной в действие в 1972 году. В настоящее время данный вид относительно простой формы множественности процессов представлен на всех уровнях организации современной вычислительной техники: от фактической многопроцессорности современных микропроцессоров до сверхпроизводительных систем с массовым параллелелизмом.


2. Распараллеливание с целью расширения диапазона масштабируемости решаемых задач. В качестве примера можно привести сверхбольшие базы данных, наиболее характерным примером которых является поисковая система  Google, обеспечивающая на сегодня с помощью параллельной работы около 100-та тысяч компьютеров индексирование и перманентное ранжирование в режиме реального времени около 10-ти млрд гипертекстовых документов.


3. Распараллеливание, связанное с естественной распределенностью решаемых задач, что характерно для большинства клиент-серверных систем. В рамках системы Google простейшая форма распределенности такого рода обусловлена, в частности, необходимостью поддержки и ранжирования в поисковых системах, локализованных по языкам и странам.

При переходе к гипералгоритмам актуальны все три перечисленных направления, но возникает необходимость в специфическом распараллеливании, обусловленная следующими 2-мя причинами:

- логическая множественность, ведущая преимущественно к MPMD-ветвлению алгоритмов при проверке логических условий;

- множественность числового представления, которая ведет в основном к SPMD-распараллеливанию.

Множественность представления количественных значений естественным образом реализуется многозадачностью и многопроцессностью современного программного обеспечения, многопроцессорностью структуры современных вычислительных систем, но самое главное – глобальной массовой многопроцессностью и многопроцессорностью современной сетевой инфраструктуры.

От господства алгоритма к преобладанию моделей

Переход к гипералгоритмам означает фактически отказ от классических форм представления алгоритмов, таких как традиционные блок-схемы, и переход к множественности их  описаний, что наиболее полно и адекватно на сегодня представлено в технологии Универсального Языка Моделирования (UML) [51].
Но в более общем виде переход к гипералгоритмам и соответствующей множественности представления может интерпретироваться как переход от преимущественно алгоритмического описания вычислительных процессов в частности, а также сложных систем и процессов вообще, к преимущественно модельной (т.е. комплексной по сути) форме их представления.
В наиболее радикальной постановке данная концепция (но без привязки к обобщенному кодо-логическому базису и гипералгоритмам) сформулирована Нариньяни А.С. в ряде его работ [52, 53].  При этом он отмечает два важных различия в подходах, определяющих преимущества модельного подхода:

- Во-первых, алгоритм и недоопределнность – это практически несовместимые понятия, а модель вполне может быть недоопределенной.
- Во-вторых, традиционный (не интервальный) алгоритм позволяет получать только отдельные точечные решения, а модель в общем случае определяет пространство решений.

Как видим и в этом случае определяющими являются те свойства моделей, которые являются специфическими и характерными для гиперлогики и гиперкодов.
В заключение следует отметить, что и в технологиях программирования наметилась тенденция к созданию приложений  на базе разработки их моделей (Model Driven Architecture архитектура - MDA). Концептуальной основой появления MDA стали спецификации объектно-ориентированного программирования, типичным примером которых является CORBA. А перевести данный круг идей в практическую плоскость также предполагается на базе технологий объектно-ориентированного программирования и UML [54]. В целом такого рода процессы вполне могут рассматриваться как практическая реализация тех концепций, о которых пишет А.С.Нариньяни, и которые свидетельствуют о назревания своего рода кодо-логической революции в развитии компьютерных технологий, моделирования и представления знаний.

Заключение

Таким образом,  рассмотренные в данной работе основные вопросы, связанные с развитием, текущим состоянием и ближайшими перспективами концепции обобщенного кодо-логического базиса, позволяют предположить, что актуальность исследования и разработок в данном направлении будет в дальнейшем возрастать, что в конечном итоге может привести к определенному качественному скачку в развитии компьютерного моделирования, а также – технологий  кодирования и представления знаний.

 

Литература

1. Аноприенко А. Я. Рекурсивное разбиение пространства при описании трехмерных объектов для визуализации в реальном времени // Материалы 4-го научно-технического семинара “Математическое обеспечение систем с машинной графикой”. - Устинов. - 1986. - С. 5-6.
2. Аноприенко А.Я. Повышение производительности систем генерации изображений: структуры и алгоритмы на уровне регенерационной памяти. Автореферат диссертации на соискание ученой степени кандидата технических наук по специальности 05.13.13. – Киев, 1987. – 20 с.

3. Аноприенко А.Я., Башков Е.А., Запоминающее устройство с многоформатным доступом к данным. А.с. 1336109 (СССР) / Опубл. 1987, БИ № 33.

4. Аноприенко А.Я., Башков Е.А., Запоминающее устройство с многоформатным доступом к данным. А.с. 1355997 (СССР) / Опубл. 1987, БИ № 44.
5. Моисеев Н.Н. Алгоритмы развития (серия «Академические чтения»). – М: Наука, 1987. – 304 с.

6. Аноприенко А.Я., Кухтин А.А. О некоторых возможностях расширения логического базиса информатики. / В кн.”Тези доповiдей мiжнародноi науково-практичноi конференцii “Iнформатизацiя в умовах переходу до ринку”, Киiв, 5-6 листопада 1992 р., с. 30-32.

7. Аноприенко А.Я. Тетралогика и тетракоды. / В кн. “Сборник трудов факультета вычислительной техники и информатики”. Вып.1. Донецк, ДонГТУ, 1996, с.32-43.

8. Аноприенко А.Я. Расширенный кодо-логический базис компьютерного моделирования / В кн. “Информатика, кибернетика и вычислительная техника (ИКВТ-97). Сборник научных трудов ДонГТУ.” Выпуск 1. Донецк, ДонГТУ, 1997, с. 59-64.

9. Анопрієнко О., Кривошеєв С. Тетракоди: новий метод кодування сигналів і зображень. / В кн. “Оброблення сигналів і зображень та розпізнавання образів. Праці Всеукраїнської міжнародної конференції УкрОБРАЗ’96. Київ, 1996, с. 15-17.

10. Аноприенко А. Я., Кривошеев С. В., Приходько Т. А. Тетракоды в кодировании и распознавании образов // Сборник научных трудов ДонГТУ. Серия “Информатика, кибернетика и вычислительная техника". Выпуск 1 (ИКВТ-97). - Донецк: ДонГТУ. - 1997. - С. 99-104.

11. Аноприенко А.Я. О некоторых приложениях стохастической геометрии к анализу и синтезу вычислительных систем и алгоритмов // Сборник трудов факультета вычислительной техники и информатики. Вып.1. - Донецк: ДонГТУ. - 1996. - С. 129-137.

12. Святный В.А., Цайтц М., Аноприенко А.Я. Реализация системы моделирования динамических процессов на параллельной ЭВМ в среде сетевого графического интерфейса // Вопросы радиоэлектроники, серия “ЭВТ”, вып. 2. - 1991. - С. 85 - 94.

13. Аноприенко А.Я., Святный В.А. Универсальные моделирующие среды // Сборник трудов факультета вычислительной техники и информатики. Вып.1. - Донецк: ДонГТУ. - 1996. - С. 8-23.

14. Аноприенко А.Я., Святный В.А. Высокопроизводительные инфомационно-моделирующие среды для исследования, разработки и сопровождения сложных динамических систем // Научные труды Донецкого государственного технического университета. Выпуск 29. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" - Севастополь: «Вебер». - 2001. - С. 346-367.

15. Аноприенко А. Я. Эволюция алгоритмического базиса вычислительного моделирования и сложность реального мира // Научные труды Донецкого национального технического университета. Выпуск 52. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2002): Донецк: ДонНТУ, 2002. – C. 6-9.

16. Anoprienko A., Svjatnyi V., Reuter A. Extended logical and numerical basis for computer simulation / “Short Papers Proceedings of the 1997 European Simulation Multiconference ESM'97. Istanbul, June 1-4, 1997" - Istanbul, SCS, 1997, p. 23-26.

17. Anoprienko A. Interpretation of some artefacts as special simulation tools and environments / “Short Papers Proceedings of the 1997 European Simulation Multiconference ESM'97. Istanbul, June 1-4, 1997" - Istanbul, SCS, 1997, p. 23-26.

18. Anoprienko A. Tetralogic and tetracodes: an effective method for information coding // 15th IMACS World Congress on Scientific Computation, Modelling and Applied Mathematics. Berlin, August 24-29, 1997. Vol. 4. Artificial Intelligence and Computer Science. - Berlin: Wissenschaft und Technik Verlag. - 1997. - P. 751-754.

19. Аноприенко А.Я. Компьютерное исследование феноменов астроморфного моделирования в контексте когнитивно-культурной эволюции // Научные труды Донецкого государственного технического университета. Выпуск 29. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" - Севастополь: «Вебер». - 2001. - С. 327-345.

20. Аноприенко А.Я. От вычислений к пониманию: когнитивное компьютерное моделирование и его практическое применение на примере решения проблемы Фестского диска / В кн. “Информатика, кибернетика и вычислительная техника (ИКВТ-99). Сборник научных трудов ДонГТУ.” Выпуск 6. Донецк, ДонГТУ, 1999, с. 36-47.

21. Аноприенко А.Я. Восхождение интеллекта: эволюция монокодовых вычислительных моделей // Научные труды Донецкого государственного технического университета. Выпуск 15. Серия "Информатика, кибернетика и вычислительная техника" (ИКВТ-2000). - Донецк: ДонГТУ. - 2000. - С. 87-107.

22. Anoprienko A. Archaeosimulation: new sight on ancient society and lessons for computer era / Problems of Simulation and Computer Aided Design of Dynamic Systems. Scientific Papers of Donetsk State Technical University. Vol. 29. – Sevastopol: Weber, 2001. P. 320-326.

23. Anoprijenko A. The early history of simulation in Europe: scale planetariums and astromorphic models // EUROSIM 2004: 5th EUROSIM Congress on Modeling and Simulation. 06–10 September 2004. ESIEE Paris, Marne la Vallee, France. Book of abstracts. S. 146-147.

24. Аноприенко А. Я. Модельная и компьютерная поддержка принятия решений в ситуации когнитивного конфликта: рассмотрение на примере сравнительного анализа гипотез о локализации Атлантиды Платона // Научные труды Донецкого национального технического университета. Выпуск 52. Серия "Проблемы моделирования и автоматизации проектирования динамических систем" (МАП-2002): Донецк: ДонНТУ, 2002. – C. 177-243.

25. Gilles E.D., Kienle A., Waschler R., Sviatnyi V., Anoprienko A., Potapenko V. Zur Entwicklung des Trainingssimulators einer gro?chemischen Anlage // Problems of Simulation and Computer Aided Design of Dynamic Systems (SCAD-2002). Scientific Papers of Donetsk National Technical University. Volume 52. Donetsk, 2002, pages 23-26.

26. Аноприенко А.Я., Забровский С.В., Потапенко В.А. Использование технологии CORBA в распределенном моделировании сложных технологических систем / Наукові праці Донецького державного технічного університету. Серія “Обчислювальна техніка та автоматизація”. Випуск 38. - Донецьк, ДонДТУ, 2002, с. 186-190.

27. Аноприенко А.Я., Потапенко В.А. Опыт создания распределенных моделирующих сред // Труды международной научно-технической конференции «Современные средства автоматизации и компьютерно-интегрированные технологии». - Краматорск 2003.

28. Святный В.А., Аноприенко А.Я., Потапенко В.А. Модульные среды для сетевого распределенного моделирования сложных динамических систем // Труды международной конференции «Современные проблемы информатизации в технике и технологиях»: Выпуск 8. – Воронеж, 2003. – С. 122-123.

29. Anoprienko A., Potapenko V. Web-basierte Simulationsumgebung mit DIVA-Serverkomponente fur komplexe verfahrenstechnische Produktionsanlagen // 17. Symposium “Simulationstechnik” ASIM 2003, Magdeburg, 16.09 bis 19.09.2003. – SCS-Europe, 2003. S. 205-208.

30. Карпенко А.С. Логика на рубеже тысячелетий // Online Journal “Logical Studies”, N5 (2000) < http://ihtik.lib.ru/philsoph/ihtik_131.htm>.

31. Gabbay D. M. (ed.) What is a logical system? Oxford: Clarendon Press (and New York), 1994.

32. Wang Hao. What is logic? // The Monist. 1994. Vol. 77. N 3. P. 261-277.

33. Hintikka J. What is true elementary logic? // Gavroglu K., Stachel J., Wartofsky M. (eds.), Physics, philosophy and the scientific community. Dordrecht: Kluwer. 1994. P. 301-326.

34. Batens D. Inconsistency-adaptive logics and the foundation of non-monotonic logic // Logique et Analyse. 1994. N 145. P. 57-94.

35. Zadeh L. A. Soft computing and Fuzzy Logic. Software Engineering Journal, November, 1994.

36. Bezdek. Editional . Fuzzy models – what are they and why? IEEE Trans. on Fuzzy systems. Vol. 1. No. 1, February, 1993.

37. Ященко А. NexGen History

38. Виджаян Дж. В ожидании Itanium // Еженедельник "Computerworld", #05, 2001 год // Издательство "Открытые системы"

39. Воеводин В.В., Воеводин В.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002. – 608 с.

40. Куроуз Дж., Росс К. Компьютерные сети: Многоуровневая архитектура Интернет. – СПб.: Питер, 2004. - 765 с.

41. Кастельс М. Галактика Интернет. – Екатеринбург: У-Фактория, 2004. 328 с.

42. Немнюгин С., Стесик О. Параллельное программирование для многопроцессорных вычислительных систем. – СПб.: БХВ-Петербург, 2002. 400 с.

43. Орфали Р., Харки Д., Эдвардс Д. Основы CORBA. –М.: МАЛИП, Горячая Линия – Телеком, 1999. – 318 с.

44. История логики. – Мн.: Новое знание, 2001. – 170 с.

45. Кнут Д.Э. Искусство программирования, томи 2. Получисленные алгоритмы. – М.: Издательский дом «Вильямс», 2000. – 832 с.

46. Курант Р., Роббинс Г. Что такое математика? – М.: Просвещение, 1967. – 558 с.

47. Даан-Дальмедико А., Пейффер Ж. Пути и лабиринты. Очерки по истории математики. – М.: Мир, 1986. – 432 с.

48. Сигорский В.П. Математический аппарат инженера. – К.: «Техника», 1975. – 768 с.

49. Новиков Ф.А. Дискретная математика для программистов. – СПб: Питер, 2000. – 304 с.

50. Белов В.М., Евстигнеев В.В., Королькова С.М., Лагуткина Е.В., Суханов В.А. Интервальная кинетика химических реакций. Обратимые реакции первого порядка // Химия растительного сырья. Т. 1 (1997), N3, с.32-35 .

51. Буч Г., Рамбо Дж., Джекобсон А. Язык UML. Руководство пользователя. – М.: ДМК, 2000. – 366 с.

52. Нариньяни А.С. Модель или алгоритм: новая парадигма информационной технологии // Информационные Технологии, 1997, № 4, стр.11-16 .

53. Нариньяни А.С. Информационные технологии 21 века: на пороге революции .

54. Марков Е. Архитектура, управляемая моделью // CitCity, 15 декабря 2005 г .

EvgeniyaBV@gmail.com
http://evgeniya.dn.ua/