Моделирование постбинарных арифметических операций

Источник: Iнформатика та комп'ютернi технологiї - 2010 / Матерiали VI мiжнародної науково-технiчної конференцiї студентiв, аспiрантiв та молодих вчених. - Донецьк, ДонНТУ - 2010, с. 184-188.

В настоящее время все ЭВМ практически полностью базируются на бинарной логике и арифметике, и до недавнего времени это являлось достаточным критерием для реализации практически всех потребностей компьютерных вычислений. Но в конце ХХ века произошли качественные изменения, как в развитии логических основ, так и в области компьютерных технологий, что привело к актуальности использования вместо стандартной двоичной логики системы с другими логическими принципами [1].

Одним из таких вариантов является переход к многозначной логике, а именно к тетралогике, что позволяет реализовать свойство адаптивности в рамках подходов, характерных для традиционной бинарной логики. Тетралогика - это логика четвертого порядка, которая включает в себя кроме классических 1 ("истина") и 0 ("ложь"), также и различные парные комбинации, в частности, такие как А ("неопределенность", "неоднозначность") и М ("множественность", "многозначность").

В данной статье рассматривается идея представления данных с помощью тетракодов, в частности при представлении вещественных чисел в виде интервалов (интервальных чисел). Такой подход влияет на точность вычислений, что обеспечивает более достоверные результаты арифметических операций в ЭВМ.

На начальном этапе исследования была реализована демонстрационная flash-модель. Она позволяет наглядно увидеть актуальность применения тетралогики для представления чисел в формате с плавающей запятой в арифметических операциях. Данная модель демонстрирует операции сложения и вычитания поэтапно, точно так же, как это выполняется в арифметическом процессоре компьютера.

Вышеописанные операции, как известно, включают в себя сдвиги разрядов. А это, в свою очередь, может приводить к уменьшению точности либо потере значимости результата. Так, например, при выполнении операции вычитания на языке ActionScript может возникнуть ситуация аналогичная следующей:
20.5-20=0.4999999:

Это возникает по той причине, что даже целые числа хранятся в памяти компьютера в вещественном формате.

Другим примером может служить считывание информации из внешней среды датчиком, который хранит данные строго фиксированной разрядности. Это приводит к тому, что при поступлении на него информации, превышающей его разрядность, лишние биты будут просто отброшены, что может значительно повлиять на точность результата.

Благодаря применению тетракодов аналогичные ситуации можно отслеживать с помощью состояний "неопределенность" и "многозначность".

В разработанной модели продемонстрировано использование всех четырех состояний тетралогики. Пользователь имеет возможность запустить уже готовый пример, либо ввести числа по своему усмотрению (рис.1).

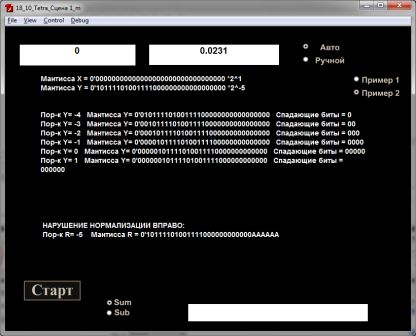
В данной модели для большей наглядности арифметических операций присутствуют два режима: авто и ручной. В режиме "авто" все этапы от начала и до конца выполняются сразу. В режиме "ручной" по каждому нажатию кнопки "Старт" выполняется один этап, что позволяет отследить принципы арифметических операций.

В будущем планируется также реализация демонстрационных моделей операций умножения и деления. Помимо этого будет создана модель, в которой будет возможность вычисления математических функций, т.к. на их примере можно исследовать интервальные вычисления.

Таким образом, хоть и данный подход влечет за собою увеличение количества бит для кодирования тетракодов в 2n раз, повышение степени информативности получаемых за счет этого кодов вполне оправдывает увеличение затрат.

Литература

[1] Аноприенко А.Я. Эволюция алгоритмического базиса вычислительного моделирования и сложность реального мира /А.Я. Аноприенко // Научные труды Донецкого национального технического университета. Серия: Проблемы моделирования и автоматизации проектирования динамических систем (МАП-2002). - 2002. - Вып. 52. - C. 6-9.

[2] IEEE Standard for Floating-Point Arithmetic (IEEE 754) http://en.wikipedia.org/wiki/IEEE_754-2008

[3] Аноприенко А. Я. Археомоделирование: модели и инструменты докомпьютерной эпохи / А. Я.Аноприенко. - Донецек: УНИТЕХ, 2007. - 318 с.

[4] Аноприенко А. Я. Тетралогика и тетракоды / А. Я. Аноприенко // Сборник трудов факультета вычислительной техники и информатики. - 1996. - Вып.1.

[5] 5. Аноприенко А.Я., Иваница С.В. Особенности постбинарного кодирования на примере интервального представления результатов вычислений по формуле Бэйли-Боруэйна-Плаффа /А.Я. Аноприенко // Научные труды Донецкого национального технического университета.Серия: Информатика,кибернетика и вычислительная техника. - 2010. - Вып.11(164). - С. 19-23.

EvgeniyaBV@gmail.com
http://evgeniya.dn.ua/