| ОБ АВТОРЕ | БИОГРАФИЯ | РЕФЕРАТ | БИБЛИОТЕКА | ССЫЛКИ | ОТЧЕТ О ПОИСКЕ | ИНДИВИДУАЛЬНЫЙ РАЗДЕЛ |
Sun Microsystems, Inc., 901 San Antonio Road, UMPK16-304, Palo Alto, CA 94303-4900, USA
Источник: E. Loh and G. W. Walster. Rumps example revisited. Reliable Computing, 8:245248, 2002.
Введение
Пример Румпа - это компьютерное выражение:
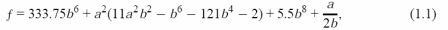
где a = 77617 и b = 33096. На IBM S/370 вычисление функции (1.1) с использованием арифметики одинарной, двойной и расширенной точности дает результат:
Одинарная точность: f = 1.172603...
Двойная точность: f = 1.1726039400531...
Расширенная точность: f = 1.172603940053178...
Это позволяет предположить, что надежный результат - примерно 1.172 603
или даже 1.1726039400532. Однако на самом деле, правильный результат (в пределах одной единицы
последней цифры) является:
f = -0. 827396059946821368141165095479816...
Даже знак был не правильный.
Этот пример часто приводится (см., например, [1], [3]) в литературе для иллюстрации того, что увеличение точности не всегда выявляет численную нестабильность там, где должна интервальная арифметика. Другие подобные примеры не известны авторам. Как отмечалось в [1], ** поразительные результаты установленные Румпом , не появляются на различных современных компьютерах. Для настоящей работы, авторы проверили результаты Румпа и выяснили, что они не дублируются при использованием арифметики стандарта IEEE 754 и любых режимов округления, в том числе наиболее распространенного - округлые до ближайшего. Результаты, полученные в Forte Developer 6 Update 2 Fortran 95 compiler from Sun microsystems Inc. [2]:
32-bit: f = -6.338253E + 29
64-bit: f = -1.1805916207174113E + 21, (1.3)
128-bit: f = +1.1726039400531786318588349045201838.
Эти результаты еще менее правильны, чем результаты Румпа. Тем не менее, использование расширенной точности предупреждает, что вычисления нестабильно. Это говорит о том, что, возможно IEEE арифметика, в отличие от S/370 IBM, показывает численную неустойчивость. Хотя во многих случаях увеличение точности числа с плавающей запятой может привести к численной неустойчивости. Существуют численные примеры. Например, следующие перестановки в выражении Румпа приводят к начальным результатам на IEEE-754 компьютерах:
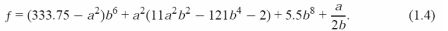
32-bit: f = 1.172604
64-bit: f = 1.1726039400531786, (1.5)
128-bit: f = 1.1726039400531786318588349045201838.
Даже это переформулированное выражение не вполне стабильно. Разные вариации в результате могут возникнуть и для альтернативных способов округления, округление точности, арифметических форматов (таких как 96-разрядных слов), или экспоненциального метода оценки.
Анализ
Значения a и b в (1.1.) удовлетворяют уравнению:
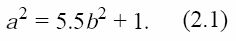
Анализ, использовавший (2.1) показывает, что члены высшего порядка
в (1.1) и (1.4) в результате приводят к
f = a/2b - 2 = -0.827396059946821368141165095479816... (2.2)
Член a/2b в оригинальном выражение Румпа и в (1.4) бросается в глаза. Член -2 возникает только после сокращения членов a2 и b2. Это свидетельствует о более понятной форме выражения в (1.1) и (1.4):

| IEEE длина слова | Диапазон | Точность |
| 32 бита | 2^127 | 23 бита |
| 64 бит | 2^1023 | 52 бита |
| 128 бит | 2^16383 | 112 бит |
| Выражение | ||||
| (1.1) | (1.4) | (2.3) | (2.2) | |
| 32 бита | 6.3E+30 | 4.4E+30 | 3.2E+30 | 1.2E-07 |
| 64 бит | 1.1E+22 | 7.1E+21 | 5.9E+21 | 2.2E-16 |
| 128 бит | 5.1E+03 | 3.1E+03 | 5.1E+03 | 1.9E-34 |
Из всех четырех режимов округления IEEE, режим с плавающей точкой в (2.3)
находятся в пределах 1 ulp от того, чтобы быть такими же, как в (1.5). Однако, (2.3) выявляет
катастрофическую потерю значащих разрядов, которая скрыта в исходном примере Румпа.
Отметим, что окончательный результат в (1.1), (1.4) и (2.3) имеет порядок 1, но самые большие
члены имеют размер 5.5b^8 = 7.9171105E + 36, что почти равно 2^123.
Таким образом, пример Румпа требует арифметику с плавающей запятой, которая имеет динамический диапазон по меньшей мере 2123 бита, чтобы не возникло переполнение. Точность, которая меньше 123 бит, вызывает потерю значащих разрядов. Эти условия выполняются по стандарту IEEE арифметики с 32 -, 64 - и 128-битной точности, как указано в таблице 1.
Однако, как упомянуто в обсуждении после (1.5), вышеупомянутые условия только необходимы и не достаточны для того, чтобы привести к результату Румпа.
Надо сказать, что оценивая (1.1), (1.4), и (2.3) с использованием интервальной арифметики в компиляторе f95 [5], производит к широким интервалам, которые содержат корректный ответ, и, таким образом, выявляет нестабильность. Как и ожидалось, увеличения точности сужает ширину результирующих интервалов. См. таблицу 2.
Благодарности
Благодарим Рууд Ван-дер-Пас за проверку исходного примера Румпа с использованием IEEE арифметики и обнаружения того, что ожидаемые результаты не производятся.
Благодарим Алексея Агафонова за выполнение различных тестов с разной точностью чисел с плавающей запятой.
Благодарим рецензентов за полезные замечания и предложения.
Литература
1. Cuyt A., Verdonk, B., Becuwe S., and Kuterna, P.: A Remarkable Example of Catastrophic
Cancellation Unraveled, Computing 66 (2001), pp. 309-320
2. ForteT Developer 6 Fortran 95 Update 2, Sun Microsystems, 2001.
3. Hansen, E. R.: Global Optimization Using Interval Analysis, Marcel Dekker, New York, 1992.
4. Rump, S. M.: Algorithms for Verified Inclusions: Theory and Practice, in: Moore, R. E. (ed.),
Reliability in Computing: The Role of Interval Methods in Scientific Computing, chapter 1, Computer
Arithmetic and Mathematical Software, Academic Press, Boston, 1988, pp. 109-126.
5. Walster, G. W.: Interval Arithmetic Programming Reference: ForteT WorkShop 6 Update 2
Fortran 95, Sun Microsystems, 2001.

