Использование fuzzy-фильтрации для понижения импульсного и гауссовского шумов в черно-белых и цветных изображениях
Авторы: Arunkumar S., Tej Akula R., Gupta R., Vimala Devi M.R.Перевод с английского языка: Гридин Д.А.
Источник: International Journal of Recent Trends in Engineering, Vol. 1, No. 1, May 2009
1. Введение
Обработка изображений является обычным приемом для того чтобы сделать изображение более детализированным и четким для человеческого глаза. Каналы передачи, из-за присущих им дефектов, могут являться причиной искажений цифровых изображений. Во многих случаях изображения зашумлены, т.е. изображения искажены в некоторых местах, в других же они свободны от шумов. Существуют три основные разновидности шумов: импульсный, гауссовский и мультипликативный. В данной статье рассматривается понижение импульсного и гауссовского шумов. Мультипликативный шум возникает, когда изображение искажено с различной степенью интенсивности в зависимости от уровней сигналов исходного изображения. С такими шумами значительно труднее бороться. В литературе [3], [4], встречается большое количество методов для удаления импульсных шумов в черно-белых и цветных изображениях. Но очень мало методов разработано для удаления гауссовского шума в цветных изображениях [1]. Большинство предложенных на данный момент фильтров применяюстя только для черно-белых изображений. Известно, что разработанные методы фильтрации могут быть применены для цветных изображений для каждой из цветовых компонент отдельно, но так же ясно, что это может привести к частичной потере деталей изображения. В этой статье мы предлагаем новый метод fuzzy фильтрации для удаления гауссового шума из цветных изображений. Он так же может быть эффективно использован для понижения импульсного шума. Возможности классических фильтров часто колеблются, в отличии от fuzzy-фильтров. Структура статьи следующая: в разделе 2а рассмотрены уже существующие методы [1], [2], [3], а раздел 2б посвящен разъяснениям предложенных фильтров. Наблюдения, сравнительный анализ и результаты экспериментов приведены в разделе 3. Выводы в разделе 4.
2. Fuzzy-фильтры2.A Существующие методы
Предположим, что исходное изображение I(x,y) повреждено гауссовским шумом со значением дисперсии σ. Тогда после обработки зашумленного изображения получаем
(1)
где О(х,у) – результат fuzzy-фильтрации, W(x,y) – взвешенная функция. Окрестность пикселя определяется координатами 'i' и 'j'. Имея различные взвешенные функции W, можно разработать разные fuzzy-фильтры [3].
2.A.1 Медианный фильтр
В случае обычного медианного фильтра значение центрального пикселя окна заменяется срединным значением соответствующей окрестности.
2.А.2 Фильтр скользящее среднее
В случае обычного фильтра скользящего среднего значение центрального пикселя окна заменяется средним значением соответствующей окрестности.
2.А.3 ATMED
АTMED – аббревиатура от Ассиметрического Триангулярного Медианного фильтра. В окрестности пикселя фильтр учитывает отклонение значения пикселя от срединного значения и заменяет пиксель шума результирующим пикселем, который получается посредством использования триангулярных функций принадлежности.
(2)
где Imax(x,y), Imin(x,y), Imed(x,y) – максимальное, минимальное и срединные значения в окрестности.
2.A.4 ATMAV ATMAV – аббревиатура от Ассиметрического Триангулярного фильтра скользящее среднее. В окрестности пикселя фильтр учитывает отклонение значения пикселя от среднего значения и заменяет пиксель шума результирующим пикселем, который получается посредством использования триангулярных функций принадлежности.
(2)
где Imax(x,y), Imin(x,y), Imav(x,y) – максимальное, минимальное и среднее значения в окрестности.
3.Предложенные фильтры3.Б.1 Фильр Probor
Фильтр Probor выполняет усредняющую операцию, но он так же учитывает важные детали изображения, такие как контуры, которые не должны уничтожаться после фильтрации. Первый под-фильтр должен отличать различия в разных областях изображения, вызванные шумом или контурами. Это может быть достигнуто при помощи использования двумерных расстояний между парами цветов и парами цветов вида (красный-зеленый), (красный-синий) и (синий-зеленый). Основная идея заключается в назначение больших весовых коэффициентов к пикселям окрестности, значения которых похожи на значение центрального пикселя и малых весов пикселям, значения которых сильно отличаются. Расстояния рассчитываются для всех пикселей окна, так же определяется максимальное значение во всей окрестности и вычисляются значения весов маски. В зависимости от расстояний маска имеет разные значения для разных позиций. Расстояние рассчитывается с помощью формулы Эвклида для всех комбинаций цветов. Затем определяется степень активности как разность между суммой и произведением весов. Это правило широко известно как “правило Probor”. Основные этапы реализации первого и второго под-фильтра показаны на Рис.1 и Рис.2. Причиной использования элемента коррекции (второго под-фильтра) является понижение компонент шума без уничтожения ценных деталей изображения. Так же его использование помогает в устранении возможных ошибок и помогает усреднить значение шума в изображении. Так же при использовании элемента коррекции может быть выполнен количественный анализ. Fuzzy-фильтр, описанный в [1], работает так же как и Probor фильтр в котором степень активности определяется как произведение весов пар.
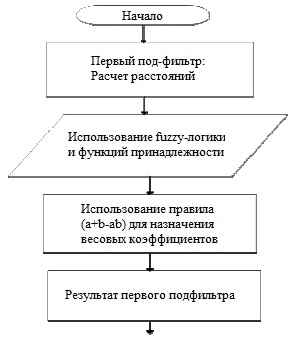 Рисунок 1 – Блок –схема первого под-фильтра (Probor фильтр)
Рисунок 1 – Блок –схема первого под-фильтра (Probor фильтр)
Результат первого под-фильтра подается в качестве входных данных на второй под-фильтр. Блок-схема представлена ниже.
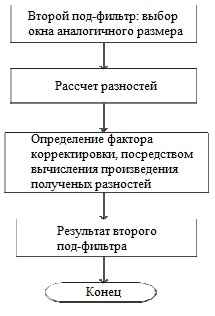 Рисунок 2 – Блок-схема второго под-фильтра (Probor фильтр)
Рисунок 2 – Блок-схема второго под-фильтра (Probor фильтр)
3.Б.2 Fuzzy-фильтр c тремя состояниями (FTS)
В этой статье предлагается новый нелинейный фильтр – Fuzzy-фильтр с тремя состояниями. Он предусмотрен для сохранения деталей изображения и вместе с тем для эффективной борьбы с гауссовским шумом. Объединим ATMED, ATMAV и медианный фильтры, в структуру обнаружения шума для определения является ли пиксель поврежденным или нет до того как будет применена фильтрация. Фильтр заменяет пиксель зашумленного изображения на результирующий, который вычисляется на основании порога определяемого fuzzy-логикой.
 Рисунок 3 – Схема FTS фильтра
Рисунок 3 – Схема FTS фильтра
Обнаружение шума реализовано с помощью гауссовского детектора, который сравнивает результаты ATMED и ATMAV фильтров с исходным или центральным пикселем для выбора одного из трех вариантов. Логика переключения приведена на рисунке выше. После того как выбор осуществлен, fuzzy-фильр использует следующее правило для получение результатов.

где, d1=abs(I(x,y)-Atmav(x,y)), d2=abs(I(x,y)-Atmed(x,y)), T – порог. Порог рассчитывается с использованием fuzzy-логики и принимает значения в пределах [0,1]. Переменные d1 и d2 разделяются на три региона: малый, средний и большой. Это реализуется простыми правилами, например “Если d1 малый и d2 малый, то результат - малый”. Похожие правила используются и для других регионов. Всего для определения порога используется девять правил. Для цветных изображений они применяются отдельно для каждой компоненты R, G, и B.
4.Результаты экспериментовФильтры, описанные в разделах 2 и 3 хорошо работают как с цветными так и с черно-белыми изображениями. Для демонстрации эффективность работы фильтров предоставлены результаты работы с цветными изображениями. Фильтры были применены к набору цветных изображений и соответствующие значения среднеквадратичного отклонения определены для различных уровней гауссовского шума. Все фильтры реализованы в Matlab 7. Результаты испытаний показаны на изображении “Lena”, поврежденном гауссовским шумом, и на изображении “Flower”, поврежденном импульсным шумом на Рис.3 и Рис.4. Среднеквадратичное отклонение используется в качестве показателя эффективности работы фильтра. Значения PSNR для изображения “Flower”, поврежденного импульсным шумом, показаны в таблице 1. Фильтр Probor позволяет получить лучшее среднеквадратичное отклонение. Значения PSNR для изображения “Lena”, поврежденного гауссовским шумом, показаны в таблице 2 для различных значений дисперсии σ.
 Рисунок 4 – Результаты эксперимента над изображением поврежденным импульсным шумом а) Зашумленное изображение (20%) б) ATMED в) ATMAV г) Fuzzy-фильтр д) фильтр Probor е) FTS фильтр
Рисунок 4 – Результаты эксперимента над изображением поврежденным импульсным шумом а) Зашумленное изображение (20%) б) ATMED в) ATMAV г) Fuzzy-фильтр д) фильтр Probor е) FTS фильтр
Таблица 1 – Результаты для изображения “Flower”
| Тип фильтра | 5% | 15% | 20% | 25% |
| ATMED | 28.29 | 26.45 | 25.26 | 23.55 |
| ATMAV | 27.55 | 26.85 | 26.72 | 26.65 |
| Fuzzy filter | 24.09 | 21.06 | 19.89 | 19.49 |
| FTS | 27.18 | 27.68 | 26.71 | 25.99 |
| Probor | 24.49 | 20.89 | 18.73 | 18.5 |
Таблица 2 – Результаты для изображения “Lena”
| Тип фильтра | σ(10) | σ(200) | σ(500) | σ(650) |
| ATMED | 179.7 | 180.2 | 182.2 | 184.5 |
| ATMAV | 179.8 | 180.1 | 182.2 | 184.3 |
| Fuzzy filter | 179.8 | 181.1 | 184.2 | 185.9 |
| FTS | 163.4 | 164.4 | 169.3 | 177.7 |
| Probor | 138.5 | 139.0 | 141.3 | 144.3 |
 Рисунок 5 – Результаты эксперимента над изображением поврежденным гауссовским шумом
Рисунок 5 – Результаты эксперимента над изображением поврежденным гауссовским шумом