|
ГЕНЕТИЧЕСКИЕ АЛГОРИТМЫ перевод Гришковец В.А. Донецкий национальный технический университет Кафедра автоматизированных систем управления |
|
Источник: http://citeseerx.ist.psu.edu |
|
Введение Генетические алгоритмы - поисковые методы, базирующиеся на принципах природной селекции и генетики. Мы начнем с краткого введения в простые генетические алгоритмы и связанную с ними терминологию. Генетические алгоритмы кодируют переменные решения поиска проблем в строках конечной длины определенного количества элементов. Строки, которые являются вариантами решений поиска проблем передаются как хромосомы, алфавит передается как гены и значения ген называются аллели. Например, в такой проблеме как путешествие коммивояжера, хромосомы представляют путь, и ген должен представлять город. В отличии от традиционны оптимизирующих методов, генетические алгоритмы работают с кодируемыми параметрами вместо непосредственно самими параметрами. Чтобы выделить хорошие решения и реализовать естественный отбор, мы нуждаемся в критерии для того, чтобы отличить хорошие решения от плохих решений. Критерий должен быть целевой функцией, которая является математической моделью или компьютерным моделированием, или это может быть функцией подцели, где люди выбирают лучшее решение из худших. В основном, критерий фитнес функции должен определять родителя относительно решения функции, которая будет впоследствии пользоваться генетическим алгоритмом для развития хороших решений. Другая важная концепция генетического алгоритма в понятии популяции. В отличии от традиционных методов поиска, генетические алгоритмы полагаются на популяцию родительских решений. Размер популяции, который есть обычным пользовательским специфическим параметром, одним из важных факторов, влияющих на масштабируемость и производительность генетического алгоритма. Например, популяция маленьких размеров может вести к преждевременной сходимости и привести к нестандартным решениям. С другой стороны, популяции большого размера ведут к ненужным расходам ценного вычислительного времени. Как только проблема решена способом хромосом и был выбран критерий, чтобы отличить хорошее решение от плохого, мы можем начать развивать поиск проблемы используя следующие шаги: 1. Инициализация. Начальная популяция искомого решения обычно генерируется в случайном порядке в пространстве поиска. Однако, знание уникальной области или другой информации может быть легко объединены. 2. Оценка. После того как популяция была проинициализирована или совокупность популяции была создана, оценивается значение фитнесс-функции варианта решения. 3. Селекция. Выбор выделяет больше копий тех решений, чем выше значения фитнесс-функции, и таким образом помещает механизм "выживания" наиболее приспособленного на варианты решения. Отдать предпочтение лучшим решениям является основной идеей селекции, и многие процедуры селекции были предложены, чтобы выполнить эту идею, включая выбор колеса рулетки, стохастический универсальный выбор, оценивая выбор и выбор турнира, некоторые из которых описаны в следующем разделе. 4. Рекомбинация. Рекомбинация комбинирует часть двух или более родительских решений, создавая новое, возможно лучшие решения. Много путей выполнения этого (некоторые из которых обсуждены в следующем разделе), и соответствующая производительность зависит от разработанного механизма рекомбинации. Потомство после рекомбинации не будет идентично любому определенному родителю, а вместо этого объединит родительские черты в новый образ. 5. Мутация. После операции рекомбинации на двух или более родительских хромосом, производится мутация локально, но произвольно модифицируя решение. Снова, большое количество вариантов решений, но это обычно включает одно или более изменений, произведенных в черте или чертах индивидуумов. Другими словами, мутация выполняет случайный обход в близи варианта решения. 6. Замена. Совокупность популяции, создаваемая селекцией, рекомбинацией, и мутацией, заменяет исходную родительскую популяцию. Много методов замены, таких как элитарная замена, замена генерацией и установившиеся заменяющие методы используются в генетических алгоритмах. 7. Повторять шаги 2-6 пока не будет соблюдено завершающее условие. Голдберг(1983, 1999, 2002) уподобил генетические алгоритмы механистическим версиям определенных режимов человеческого новшества и показал, что эти операторы, когда анализируют индивидуально – неэффективны, но когда объединены вместе они могут хорошо работать. Этот аспект был объяснен с понятием фундаментальной интуиции и интуиции новшества. То же самое исследование сравнивает комбинацию селекции и мутации к непрерывному совершенствованию (форма восхождения на вершину), и комбинация селекции и рекомбинации к новшеству(перекрестное оплодотворение). Эти аналогии были использованы при разработке методологии разложения проекта и так названы соответствующие генетические алгоритмы, которые решают тяжелую проблемы быстро, достоверно. Эта глава организована следующим образом. Следующая секция обеспечивает детали отдельных шагов типичного генетического алгоритма и представляет несколько популярных генетических операторов. Раздел 4.1.2 представляет принципиальную методологию проектирования соответствующих генетических алгоритмов, основанных на принципах разложения. Раздел 4.1.3 дает краткий обзор проектирования принципиальных методов повышения эффективности, чтобы ускорить генетические и эволюционные алгоритмы. Методы селекции Пропорциональный выбор фитнесс-функции. Он включает методы такие как колесо рулетки(Голландия, 1975; Голдберг, 1989) и стохастический универсальный выбор(Бейкер, 1985; Грефенстейт и Бейкер, 1989). Выбор в колесе рулетки, каждый индивид в популяции назначал часть колеса рулетки, измеренную в пропорции к ее фитнесс-функции. Так, в колесе рулетки хорошее решение имеет больший размер сектора чем меньше приспосабливаемые решения. Колесо рулетки крутят, чтобы получить представителя воспроизводства. Колесо рулетки выбирает схему, которая может быть осуществлена следующим способом: 1. Найти значение фитнесс-функции, fi , для каждого индивидуума популяции. 2. Вычислить вероятность(размер сектора), pi ,выбор каждого участника популяции: pi = fi / sum(fj) , где n размер популяции. 3. Вычислить совокупную вероятность, qi ,для каждого индивидуума: qi = sum(pi) 4. Сгенерировать случайное число, r Є (0, 1]. 5. Если r < q тогда выбирается первая хромососма х1, иначе выбирается индивидум Хi, который Qi-1 < r < Qi 6. Повторить шаги 4-5 n раз создавая n представителей в последующую совокупность хромосом. Порядковый Выбор Он включает методы, такие как выбор турнира и выбор усечения. В турнире выбора, s хромосом выбираются случайно( с или без замены) и включаются в турнир друг против друга. Лучшие особи в группе из k хромосом побеждают в турнире и выбираются как родители. Наибольшее используется значение s=2. Используя эту схему выбора, в n турнирах должны выбираться n особей. 4.1.1.2 Оператор рекомбинации(Кроссовер) После отбора, особи из популяции преобразовываются и получаются новые, в надежде на лучшее потомство. В литературе по генетическим алгоритмам, много методов кроссовера имеют разработки и некоторые из них описаны в этой главе. Много операторов рекомбинации использовались в литературе как специфические проблемы и в этой главе мы будем представлять некоторые основные операторы кроссовера. Нужно отметить, что, в то время как для трудных проблем поиска, многие из следующих операторов не масштабируемые, они очень полезные как первый выбор. Недавно, однако, исследователи добились значительного успеха в проектировании масштабируемых операторов рекомбинации, которые приспосабливают редактирование, которое будет кратко обсуждено в разделе 4.1.2.  В большинстве операторов рекомбинации, 2 особи выбираются случайно и рекомбинация происходит с вероятностью pc, которая называется вероятностью кроссовера. Это однородное случайное число r, которое генерируется если r<=pc, две случайные особи подвергаются рекомбинации. Иначе, то есть, если r>pc , 2 потомка являються копиями своих родителей. Значение pc может быть установлено экспериментально, или может быть установлено основываясь на принципах теоремы. k-точечный кроссовер Одноточечный, двухточечный кроссоверы самые простые и наиболее широко использующиеся методы. В одноточечном кроссовере, который изображен на рисунке 1, точка кроссовера выбрана случайно по строковой длине, и аллелями на одной стороне точки обмениваются между особями. В двухточечном кроссовере две точки кроссовера выбираются случайно. Аллели между двумя точками меняются между особями случайно. Двухточечный кроссовер представлен также на рисунке 1. Концепция одноточечного кроссовера может быть влючена в k-точечный кроссовер, где k-точки кроссовера, которые используются вместо только один или два. Универсальный кроссовер Другой общий оператор рекомбинации универсальный кроссовер. В универсальном кроссовере, проиллюстрированном на рисунке 1. Каждая аллеля изменяется между парой в произвольном порядке выбранных хромосом с определенной вероятностью, pc , известной как вероятность свопинга. Обычно значение вероятности свопинга принято, чтобы было 0.5. Кроссовер основанный на универсальном К-точечный и универсальный методы кроссовера описанные выше не хорошо подходят для поисковых проблем с перестановкой генов, таких как используемые в проблеме коммивояжера. Они часто создают потомков, что представляют недопустимые решения для поисковой проблемы. Поэтому, когда решая поисковые проблемы с кодами перестановки, специфическая проблема - механизм восстановления, который часто требуется (и используется) в соединении с вышеупомянутым методы рекомбинации, чтобы всегда создавать допустимые варианты решения. Другая альтернатива – использовать методы рекомбинации, разработанные специально для кодов перестановки, которые всегда генерируют допустимые варианты решения. В кроссовере, основанном на универсальном, 2 родителя (скажем P1 и P2) – случайно выбранные, и случайный двоичный шаблон сгенерирован. Некоторые из генов потомков C1 заполняют беря гены от родителя P1, где он есть в шаблоне есть. В этой точке у нас есть C1 частично заполнен, но у этого есть некоторые "разрывы". Гены родителя P1 в позициях, соответствующих нулям в шаблоне, взяты и сортированы в том же самом порядке, как они появляются в родителе P2. Сортированный список привык к заполненным разрывам в C1. Потомство C2 создается при использовании подобного процесса. Оператор порядко-основанного кроссовера - изменение универсального основанного на порядке кроссовера, в котором в произвольном порядке выбраны два родителя, и сгенерированы две случайные точки. Гены между разрезающими точками копируются в детей. Начиная со второй точки кроссовера копируют гены, которые уже не присутствуют в потомстве от альтернативного родителя (родитель кроме того, гены которого скопированы потомством в начальной фазе) в порядке они появляются. Например, для потомка С1 , с аллель C, D и Е копируются из родителя P1 , мы получаем аллели B, G, F, и А из родителя Р2 . Начиная с второй точки кроссовера, которая является шестым геном, мы копируем аллели B и G как шестой и седьмой гены соответсвенно. Мы тогда переносим и копируем аллели F и А как первый и второй гены. Частично соответствующий кроссовер(ЧСК) Кроме генерирования допустимого потомства, оператор ЧСК также сохраняет упорядочивания в пределах хромосомы. В ЧСК два родителя выбираются случайно и генерируются точки кроссовера. Аллелями в двух точках кроссовера родителя обмениваются с аллелями, соответствующими отображенным другим родителем. Например, как показано на рисунке 3, посмотрим на родителя P1 , первый ген в двух точках кроссовера. Поэтому гены меняются в родителе P1. Так же мы подкачиваем 6 и 3, и 10 и 7, чтобы создать потомство C1.  После всех обменов можно заметить, что мы достигли дублирования упорядочивания одного из генов между точками кроссовера в пределах противоположной хромосомы, и наоборот. 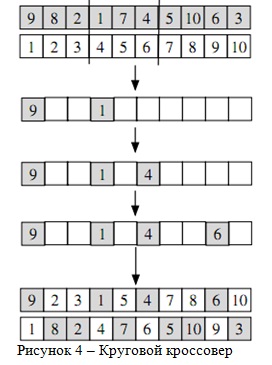 Круговой кроссовер Мы опишем круговой кроссовер с помощью простой иллюстрации. Считайте двух в произвольном порядке выбранных родителей P1 и P2 как показано в рисунке 4.5, которые являются решениями проблемы коммивояжера. Потом С1 получает первую переменную (город представления 9) от P1. Мы также выбираем переменную которая отображается на ту же самую позицию в P2. С 9 города выбираем из P1 , который находится на первом месте в P2 , мы выбираем город 1 и место это в С1 в некоторой позиции поскольку это появляется в P1 (четвертый ген), как показано в рисунке 4. Город 1 в P1 сейчас находится как город 4 в P2, так мы поставили город 4 в С1 в некоторую позицію это занимает в P1 (шестой ген). Мы продолжаем этот процесс еще раз и копируем город 6 в девятый ген C1 из P1. В этой точке. Начиная с города 6 в P1 до города 9 в P2, мы должны взять город 9 и поставить на место в С1., но это было уже сделано, таким образом, мы завершили цикл; который является, где этот оператор получает его имя. Недостающие города в потомстве C1 являются заполненными из P2. Потомства C2 создается таким же образом, начиная с первого города родителя P2 (см. рисунок 4). 4.1.1.3 Оператор мутации Если мы используем оператор кроссовера, такой как одноточечный кроссовер, мы можем взять лучшие и лучшие хромосомы, но проблема, если два родителя (или хуже, вся популяция) будут иметь ту же самую аллель в данном гене тогда одноточечный кроссовер не будет изменять это. Другими словами. у того гена будет та же самая аллель навсегда. Мутация разработана, чтобы преодолеть эту проблему, чтобы добавить разнообразие к популяции и гарантировать, что возможно исследовать все пространство поиска. В эволюционных стратегиях мутация - ключевое изменение/оператор поиска. В отличие от эволюционных стратегий, мутация часто - вторичный оператор в генетическом алгоритме, выполняемый с низкой вероятностью. Одна из наиболее распространенных мутаций – мутация «бит-щелчек». В поразрядной мутации каждый бит в двоичной строке менялась ( о преобразовывался в 1 и наоборот) с определенной вероятностью, pm , зная вероятность мутации. Как отмечалось ранее, мутация выполняет случайный обход около особи. Другие операторы мутации, такие как специфические проблемы, могут также быть разработаны и часто используются в литературе. 4.1.1.4. Замена Как только создаются новые решения потомства, используя кроссовер и мутацию, мы должны ввести их в родительскую популяцию. Есть много способов, с помощью которых мы можем приблизиться к этому. Примите во внимание, что родительские хромосомы были уже выбраны согласно их фитнесс-функции, таким образом, мы надеемся, что дочерние элементы (которые включают родителей, которые не подвергались кроссоверу) среди самых приспособленных в популяции и таким образом, мы надеялись бы что популяция будет постепенно, в среднем, увеличивать свои значения фитнесс-функции. Некоторые из наиболее распространенных заменяющих методов представлены в общих чертах ниже.
4.1.2 Компетентный генетический алгоритм В то время как использование новшества для того, чтобы объяснить рабочие механизмы генетических алгоритмов очень полезно, как метафора проекта это излагается тяжело, поскольку процессы новшества самостоятельно не хорошо поняты. Однако, если мы хотим, чтобы генетические алгоритмы все более и более успешно решали трудные проблемы через широкий спектр областей, мы нуждаемся в принципиальном, но механистическом способе разработать генетические алгоритмы. Прошлые несколько десятилетий засвидетельствовали большие шаги к разработке так называемых компетентных генетических алгоритмов — генетические алгоритмы, которые решают тяжелые проблемы, быстро, достоверно, и точно (Голдберг, 1999a). С вычислительной точки зрения, существование компетентного генетического алгогритма предполагает, что много тяжелых проблем могут быть решены масштабируемым способом. Кроме того это значительно уменьшает бремя на пользователе, чтобы выбрать хорошее кодирование или хороший генетический оператор, который сопровождает много приложений генетического алгоритма. Если генетический алгоритм может адаптироваться к проблеме, тогда есть меньше причин для пользователя, который должен адаптировать проблему, кодирование, или операторы к генетическому алгоритму. В этом разделе мы кратко рассмотрели некоторые из ключевых уроков описания компетентного генетического алгоритма. Значительно мы ограничиваем обсуждение выбора и рекомбинации генетического алгоритма и сосредоточились на типе перекрестного опыления новшества, и кратко обсудили ключевые аспекты описания компетентного генетического алгоритма . Используя Голландскую нотацию стандартного блока (Голландия, 1975), Голдберг предложил анализировать проблему разработки компетентного генетического алгоритма (Голдберг и др., 1992a). Это описание декомпозиции было объяснено подробно в другом месте (Голдберг, 2002), и кратко рассмотренно ниже. Рассмотрим процесс построения блоков генетичеких алгоритмов Ключевая идея в выборе рекомбинации в генетических алгоритмах теория состоит в том, что генетические алгоритмы работают через механизм декомпозиции и повторной сборки. Холланд (1975) названнл хорошо адаптированные наборы функций, которые были компонентами эффективных стандартных блоков решений (СБ). Основная идея состоит в том, что генетические алгоритмы неявно идентифицирует стандартные блоки, или подсистемы хороших решений, и повторно объединяются в подсистемы, чтобы сформировать очень высокопроизводительные решения. Понимание тяжелых проблем стандартних блоков С точки зрения перекрестного оплодотворения новшества, проблемы, которые трудны, есть в стандартных блоках, которые трудно получить. Это может быть то, потому что стандартне блоки сложны, трудно искать, или потому что различные стандартне болки трудно разделить, или потому что стандартне болки младшего разряда могут вводить в заблуждение или обман. Понимание стандартних блоков Рост и Синхронизация Другой ключевой идеей в этих стандартних блоках или понятия существуют в своего рода экономии конкурентного рынка идей, и шаги должны быть сделаны, чтобы гарантировать что лучшие вырастут и приймут доминирующую долю на рынке популяции, и темп роста не может быть слишком быстрым, не слишком медленным. Рост в доле на рынке может быть довольно легек (Голдберг и Сэстри, 2001), соответственно устанавливая вероятность кроссовера, pc, и давление выбора, s, так, чтобы: Понимание стандартних блоков как предоставление и принятие решений Одна роль популяции должна гарантировать достаточный запас необработанных стандартных блоков в популяции. В произвольном порядке сгенерированные популяции увеличивающегося размера, с более высокой вероятностью, будут содержать большее число более сложных стандартних блоков (Голланд, 1975; Голдберг, 1989c; Голдберг и др., 2001). Для проблемы с m стандартных блоков, каждый состоящий из k алфавитов количества элементов ?, размер популяции, n, требуемый гарантию присутствия по крайней мере одной копии всех необработанных стандартных блоков дана Голдбергом и др. (2001) как: |
 где є – вероятность срыва стандартного блока. Два других подхода использовались в понимании времени. Не уместно в основном учебном руководстве как это описать их подробно, но мы даем несколько ссылок в качестве примера для заинтересованного читателя. Модели времени поглощения, где смоделирована динамика лучшей особи. Модели интенсивности выбора, где подходы, подобные тем в количественной генетике (Bulmer, 1985), используются и смоделирована динамика среднего значения фитнесс-функции популяции. Модели времени предполагают это для проблемы размера L со всеми стандартными блоками равной важности или отчетливости, время сходимости, tc, генетического алгоритма дано Миллером и Голдбергом (1995), должно быть:
где є – вероятность срыва стандартного блока. Два других подхода использовались в понимании времени. Не уместно в основном учебном руководстве как это описать их подробно, но мы даем несколько ссылок в качестве примера для заинтересованного читателя. Модели времени поглощения, где смоделирована динамика лучшей особи. Модели интенсивности выбора, где подходы, подобные тем в количественной генетике (Bulmer, 1985), используются и смоделирована динамика среднего значения фитнесс-функции популяции. Модели времени предполагают это для проблемы размера L со всеми стандартными блоками равной важности или отчетливости, время сходимости, tc, генетического алгоритма дано Миллером и Голдбергом (1995), должно быть: 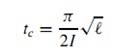 где I – интенсивность селекции, которая является параметром, зависящий от метода выбора и давления выбора. Для выбора турнюра, I может быть приближен с точки зрения s следующим отношением (Бликл и Тиле, 1995):
где I – интенсивность селекции, которая является параметром, зависящий от метода выбора и давления выбора. Для выбора турнюра, I может быть приближен с точки зрения s следующим отношением (Бликл и Тиле, 1995):  С другой стороны, если у стандартних блоках проблемы с различной отчетливостью, то время сходимости увеличивается по-другому. Например, когда проблемы по экспоненте масштабируются с определенным стандартным блоком, являющимся по экспоненте лучше, чем другие, тогда время сходимости, tc, генетического алгоритма линейно с проблемным размером и может бать представлено следующим образом:
С другой стороны, если у стандартних блоках проблемы с различной отчетливостью, то время сходимости увеличивается по-другому. Например, когда проблемы по экспоненте масштабируются с определенным стандартным блоком, являющимся по экспоненте лучше, чем другие, тогда время сходимости, tc, генетического алгоритма линейно с проблемным размером и может бать представлено следующим образом: 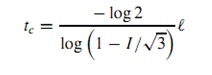
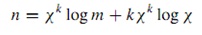 Только обеспечение необработанного предоставления недостаточно, принятие решений среди различных, конкурирующих понятий является статистическим в природе, и поскольку мы увеличиваем размер популяции, мы увеличиваем вероятность принятия самых лучших решений (Де Жонг, 1975; Голдберг и Радник, 1991; Голдберг и др., 1992a; Harik и др., 1999). Аддитивным образом проблема декомпозиции с m стандартных блоков размера k каждый, размер популяции, требуемый не только предоставление, но также и гарантирует, что корректное принятие решений приблизительно дано Harik и др. (1999) как:
Только обеспечение необработанного предоставления недостаточно, принятие решений среди различных, конкурирующих понятий является статистическим в природе, и поскольку мы увеличиваем размер популяции, мы увеличиваем вероятность принятия самых лучших решений (Де Жонг, 1975; Голдберг и Радник, 1991; Голдберг и др., 1992a; Harik и др., 1999). Аддитивным образом проблема декомпозиции с m стандартных блоков размера k каждый, размер популяции, требуемый не только предоставление, но также и гарантирует, что корректное принятие решений приблизительно дано Harik и др. (1999) как: 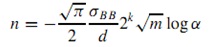 Где
Где  отношение сигнал-шум (Голдберг и др., 1992a), и a - вероятность неправильного решения среди конкурирующего, создавая блоки.
отношение сигнал-шум (Голдберг и др., 1992a), и a - вероятность неправильного решения среди конкурирующего, создавая блоки.