|
РАЗРАБОТКА КОМПЬЮТЕРИЗИРОВАННОЙ ИНФОРМАЦИОННОЙ ПОДСИСТЕМЫ ОПЕРАТИВНО-КАЛЕНДАРНОГО ПЛАНИРОВАНИЯ С ПОМОЩЬЮ МУРАВЬИНЫХ АЛГОРИТМОВ Авторы: Черный М.С, Скобцов Ю.А. Донецкий национальный технический университет Кафедра автоматизированных систем управления |
|
Общая постановка проблемы Качество функционирования современного производства во многом определяется решениями, принимаемыми на этапах календарного планирования и оперативного управления. Планирование обеспечивает взаимодействие совокупности элементов управляемого объекта для достижения заданных целей, главная из которых заключается в организации согласованного во времени и маршрутно-ориентированном пространстве движения частей и изделий в производстве. В рамках оперативного управления одной из важнейших проблем является проблема планирования загрузки оборудования, т.е. упорядочение работ на выбранной структуре производственных модулей (календарное планирование) [1]. Особенностью машиностроительной сферы является тот факт, что в процессе работы некоторое оборудование может выйти из строя, вследствие этого необходимо иметь возможность динамически перераспределять нагрузки между оставшимся оборудованием, чтобы не останавливать все производство. Постановка задачи исследования На данный момент разработано множество алгоритмов и моделей для решения задачи оперативно-календарного планирования. Большая часть этих методов не дает точного решения, а те методы, что дают точное решение, требуют больших вычислительных ресурсов и не применимы во многих случаях. В данной работе исследуется возможность применения муравьиных алгоритмов для оперативно-календарного планирования, вследствие их простоты в применении и возможности их адаптации к динамическим изменениям среды. Проблема оперативно-календарного планирования может быть характеризована как n деталей, которые должны быть обработаны на m станках. Все детали должны быть обработаны, используя конечный набор ресурсов, где ресурсами называются станки. Каждая деталь представляет собой запрос планирования ряда операций, согласно плану технологического процесса, который определяет ограничения предшествования. Мы имеем:  Для каждой операции Приведенный пример задачи мы можем связать с дизъюнктивным графом G=(V, A, E), где V набор узлов, A - соединительный набор дуг, и E - дизъюнктивный набор дуг. Узлы V соответствуют всем операциям и двум фиктивным узлам, источнику и выходом. Соединительные дуги A представляют отношения предшествования между операциями для каждой детали, а дизъюнктивные дуги E представляют все пары операций, которые будут выполнены на том же самом станке. Всем дугам, исходящих от узла, присваивается продолжительность обработки операции. У источника есть соединительные дуги с нулевой длинной для всех первых операций каждой детали, а у выхода есть соединительные дуги, исходящие из всех последних операций. Выполняемое планирование соответствует выбору одной дуги от каждой дизъюнктивной дуги и соединяется таким образом, чтобы получающийся направленный граф был нециклическим, то есть чтобы в нем не было петель. Проблема уменьшения периода обработки сводится к обнаружения ряда дизъюнктивных дуг которые минимизируют длину критического пути в направленном графе.[2] Описание муравьиных алгоритмов Для решения данной задачи были выбраны муравьиные алгоритмы (МА), которые основаны на использовании популяции потенциальных решений и разработаны для решения задач комбинаторной оптимизации, прежде всего, поиска различных путей на графах. Кооперация между особями (искусственными муравьями) здесь реализуется на основе моделирования «stigmergy». При этом каждый агент, называемый искусственным муравьем, ищет решение поставленной задачи. Искусственные муравьи последовательно строят решение задачи, передвигаясь по графу, откладывают феромон и при выборе дальнейшего участка пути учитывают концентрацию этого фермента. Чем больше концентрация феромона в последующем участке, тем больше вероятность его выбора.[3] В качестве иллюстрации возьмем задачу поиска кратчайшего пути между двумя узлами графа G=(V, E), где V – множество узлов (вершин), а E – матрица, которая представляет связи между узлами. Пусть 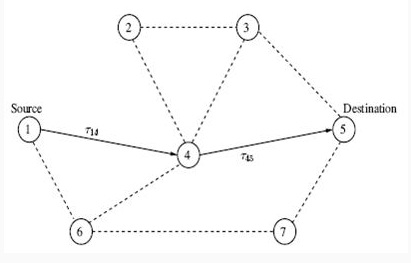 Рисунок 1 Пример продвижения по графу. Строго говоря, в начальный момент времени концентрация феромона для каждой дуги графа нулевая, но для удобства каждой дуге присваивается небольшое случайное число Муравей выбирает следующую дугу пути следующим образом. Множество муравьев
Где
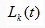 – длина пути, построенного k-м муравьем в момент времени t. Таким образом, для каждой дуги графа концентрация феромона определяется следующим образом – длина пути, построенного k-м муравьем в момент времени t. Таким образом, для каждой дуги графа концентрация феромона определяется следующим образом
где В настоящее время на основе применения муравьиных алгоритмов получены хорошие результаты для таких сложных оптимизационных задач, как задача коммивояжёра, транспортная задача, задача календарного планирования, задача раскраски графа, квадратичная задача о назначениях, задача оптимизации сетевых трафиков и ряд других. Решение задачи и результаты исследований. Для обеспечения высокой эффективности работы производственных участков необходимо составлять близкие к оптимальному расписания работы оборудования. Поэтому необходимо разработать компьютеризированную подсистему оперативно-календарного планирования работы производственного участка машиностроительного производства для повышения эффективности работы за счет составления субоптимальных расписаний работы, на основе выбранных критериев оптимизации. Поскольку в основе муравьиного алгоритма лежит моделирование передвижения муравьёв по некоторым путям, то такой подход может стать эффективным способом поиска рациональных решений для задач оптимизации, допускающих графовую интерпретацию. Был разработан алгоритм для решения задачи оперативно-календарного планирования с использованием муравьиных алгоритмов. Обобщенная схема работы алгоритма сводится к следующему:
Каждый проход по данному алгоритму формирует решение только для данного состояния цеха, т.е. при каких либо изменениях алгоритм запускается сначала, при этом возможны варианты, когда при построении нового решения есть смысл отталкиваться от прошлого оптимального решения. Определяющими при построении алгоритма является:
Приведем формализованный алгоритм работы данной системы:
Пункты 3) – 6) повторяются до тех пор, пока не будет достигнут необходимый результат. В алгоритме могут быть использованы различные критерии окончания, например:
Выводы В свете быстрых темпов развития современного производства и высоких требованиях к гибкости и способности адаптироваться к изменяющимся условиям оперативно-календарное планирование является неотъемлемой частью любого производства. Математический аппарат муравьиных алгоритмов способен удовлетворить все требования, предъявляемые современным производством, вследствие того, что он реализует поведение реальных муравьев, чье способность к адаптации к любым условиям столетиями оттачивала природа. Благодаря своей простоте, масштабируемости и динамичности муравьиные алгоритмы целесообразно использовать для решения задачи оперативно-календарного планирования.
|
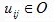 есть деталь
есть деталь 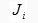 , которой она принадлежит, станок
, которой она принадлежит, станок 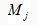 , на котором она должна быть обработана и продолжительность обработки
, на котором она должна быть обработана и продолжительность обработки 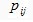 операции
операции  , где
, где 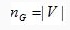 - число узлов в графе. Обозначим
- число узлов в графе. Обозначим 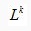 – длину пути в графе, пройденного k-м муравьем, которая равна числу пройденных дуг (скачков между вершинами) от первой до последней вершины пути. Пример графа с выделенным путем представлен на рисунке 1. С каждой дугой, соединяющей вершины (i, j) ассоциируем концентрацию феромона
– длину пути в графе, пройденного k-м муравьем, которая равна числу пройденных дуг (скачков между вершинами) от первой до последней вершины пути. Пример графа с выделенным путем представлен на рисунке 1. С каждой дугой, соединяющей вершины (i, j) ассоциируем концентрацию феромона  .
.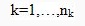 помещаются в начальную вершину. В каждой итерации МА каждый муравей пошагово строит путь до конечной вершины. При этом в каждой вершине каждый муравей должен выбрать следующую дугу пути. Если муравей k находится в вершине i, он выбирает следующую вершину
помещаются в начальную вершину. В каждой итерации МА каждый муравей пошагово строит путь до конечной вершины. При этом в каждой вершине каждый муравей должен выбрать следующую дугу пути. Если муравей k находится в вершине i, он выбирает следующую вершину 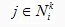 на основе вероятностей перехода
на основе вероятностей перехода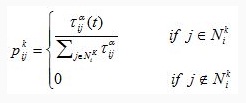 (1)
(1) представляет множество возможных вершин, связанных с вершиной i, для муравья k. Если для любого узла i и муравья k
представляет множество возможных вершин, связанных с вершиной i, для муравья k. Если для любого узла i и муравья k 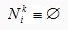 , тогда предшественник узла i включается в
, тогда предшественник узла i включается в  - положительная константа, которая определяет влияние концентрации феромона. Очевидно, большие значения
- положительная константа, которая определяет влияние концентрации феромона. Очевидно, большие значения  (2)
(2) (3)
(3) - число муравьев. Из (3) следует, что общая концентрация феромона для данной дуги пропорциальна «качеству» путей, в которые входит эта дуга, поскольку откладываемое отражает «качество» соответствующего пути [5].
- число муравьев. Из (3) следует, что общая концентрация феромона для данной дуги пропорциальна «качеству» путей, в которые входит эта дуга, поскольку откладываемое отражает «качество» соответствующего пути [5]. ;
;