УДК 681.3
РЕАЛИСТИЧНАЯ СТЕРЕО–ВИЗУАЛИЗАЦИЯ ТРЕХМЕРНЫХ СЦЕН МЕТОДОМ ТРАССИРОВКИ ЛУЧЕЙ НА СПЕЦИАЛИЗИРОВАННЫХ ПАРАЛЛЕЛЬНЫХ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМАХ
Гуров А.В., Зори С.А.
Донецкий национальный технический университет
кафедра прикладной математики и информатики
E–mail: al_gurov@mail.ru, zori@pmi.donntu.ru
Аннотация:
Гуров А.В., Зори С.А. Реалистичная стерео–визуализация трехмерных сцен методом трассировки лучей на специализированных параллельных вычислительных системах. Рассмотрена классификация методов получения стерео–изображений. Описан алгоритм обратной трассировки лучей. Определен метод ускорения алгоритма трассировки лучей, поставлены цели для дальнейшего анализа и реализации реалистичной стерео–визуализации.
Общая постановка проблемы
На сегодняшний день построение стереоизображений является одним из перспективных направлений компьютерной графики. Возможность стереопредставления изображений порождает новые направления прикладных исследований – создание программно–аппаратных комплексов виртуальной и расширенной реальности, обучающих комплексов, построение реалистичных презентаций и анимаций и пр. При этом в таких системах возникает необходимость эффективного, по скоростным параметрам, применения и совмещения как методов реалистичной трехмерной графики, использующих традиционный механизм визуализации, так и методов нетрадиционной визуализации – стереовизуализации.
Методы трассировки лучей на сегодняшний день считаются наиболее мощными и универсальными методами создания реалистичных изображений. Известно множество примеров реализации алгоритмов трассировки для качественного отображения самых сложных трехмерных сцен. Универсальность методов трассировки в значительной степени обусловлена тем, что в их основе лежат простые и ясные понятия, отражающие опыт человека по восприятию окружающего мира. Методы реализации стерео также хорошо известны и проработаны и применяются во многих практических реализациях графических систем. Целью работы является исследование возможности эффективной, по скоростному критерию, реализации реалистичного синтеза стереоскопических изображений методом трассировки лучей и возможности его реализации на параллельных архитектурах специализированных вычислительных систем.
Обзор методов построения стерео–изображений
Стерео–изображение — картина или видеоряд, использующий два отдельных изображения, позволяющих достичь стереоэффекта.
Стереоэффект (зрительный) — ощущение протяжённости пространства и рельефности, возникающие при наблюдении реальных объектов, рассматривании стереопар, стереофотографий, стереоизображений и голограмм.
Бинокулярная стереоскопия (анаглифовые очки)
Этот метод использует очки, вместо линз у которых вставлены светофильтры дополнительных цветов. Дешёвый, но достаточно эффективный метод, физически он не обеспечивает правильную передачу цвета стереоизображения, однако нервная система довольно хорошо интерпретирует его. Время адаптации зрения к этому методу составляет около 30 секунд, после длительного использования на пропорциональный период нарушается цветовосприятие.
В одном цветовом канале (например красном) передается изображение для левого глаза, в другом или двух других (например в синем и зеленом) – для правого. Для того чтобы правый глаз не увидел изображение из красного канала, а левый из сине–зеленого используются анаглифические очки в которых установлены светофильтры вместо линз (в рассматриваемом случае – для левого глаза – сине–зеленый, а для правого – красный). Как правило для создания анаглифа используются цвета стандартной схемы RGB, но возможны и другие раскладки. Распространены следующие варианты анаглифа:
– red–cyan (красный и сине–зеленый) – самый распространенный формат;
– optimized red–cyan – используется оптимизированный алгоритм получения стереоизображения, с целью достижения лучшей цветопередачи. Данный метод требует большей вычислительных мощностей видеоподсистемы;
– black–white (чернобелый) – анаглиф с оттенками серого, используется с целью получения более равномерной яркости изображения в ущерб цветопередачи;
– yellow–blue (желтый и синий) – данная комбинация цветов RGB позволяет получить неплохую цветопередачу, однако изображение получится более холодным из–за использования синего, для данного варианта необходимо использовать очки с синим и желтым светофильтрами.
Монокулярная «псевдостереоскопия»
«Качающаяся» стереоскопия. Восприятие объёма может быть получено не только с помощью одновременного рассматривания объекта или изображения двумя глазами одновременно, но и путём достаточно быстрой смены изображений в одном канале изображения (при монокулярном зрении). Похожий механизм восприятия объёма реализует и природа — например, куры, качая головой, обеспечивают высококачественное восприятие (хотя поля зрения их глаз перекрываются очень мало). Так, технология GIF–анимации позволяет создавать псевдостереоскопические объёмные изображения.
Аналогичный метод предложен и для «псевдостереотелевидения» — путём создания анаглифического изображения для движущихся, динамических объектов. Вместо одновременного рассматривания изображения, видеосигнал расщепляется по двум цветовым каналам (обычно — красный и голубой, с применением соответствующих очков). Динамическое плоское цветное монокулярное изображение обрабатывается таким образом, что на один глаз (например, красный канал) подаётся неизменный видеосигнал, а на второй (голубой канал) — подают сигнал с небольшой временно́ й задержкою, от изменившейся динамической сцены. За счёт движения объектов в сцене, человеческий мозг получает «объёмное изображение» (но только если объекты переднего плана либо смещаются, либо поворачиваются). Недостатком данного метода является ограниченность типа сцен, в которых может возникнуть стереоэффект, а также заметная потеря качества цветной картинки (каждый глаз получает почти монохроматическое цветное изображение).
Принцип работы алгоритма обратной трассировки лучей
Алгоритм работает следующим образом: из виртуального глаза через каждый пиксель изображения испускается луч и находится точка его пересечения с поверхностью сцены. Лучи, выпущенные из глаза, называют первичными. Допустим, первичный луч пересекает некий объект 1 в точке H1 (рис. 1).
Далее необходимо определить для каждого источника освещения, видна ли из него эта точка. Предположим пока, что все источники света точечные. Тогда для каждого точечного источника света, до него испускается теневой луч из точки H1. Это позволяет сказать, освещается ли данная точка конкретным источником. Если теневой луч находит пересечение с другими объектами, расположенными ближе чем источник света, значит, точка H1 находится в тени от этого источника и освещать ее не надо. Иначе, считаем освещение по некоторой локальной модели (Фонг, Кук–Торранс и.т.д.). Освещение со всех видимых (из точки H1) источников света складывается. Далее, если материал объекта 1 имеет отражающие свойства, из точки H1 испускается отраженный луч и для него вся процедура трассировки рекурсивно повторяется. Аналогичные действия должны быть выполнены, если материал имеет преломляющие свойства.
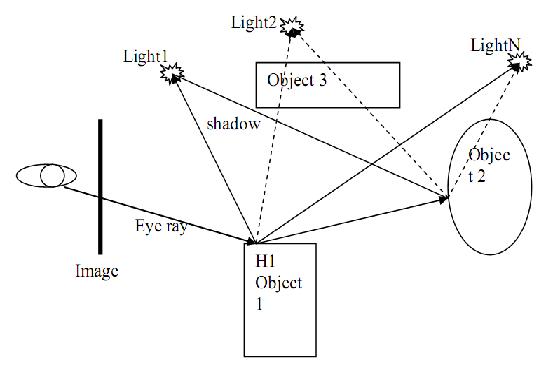
Рисунок 1 – Алгоритм трассировки лучей
Рассмотрим некоторые популярные методы ускорения алгоритма трассировки лучей.
kd–tree
Рассмотрим структуру бинарного пространственного разбиения, называемую kd– дерево. Эта структура представляет собой бинарное дерево ограничивающих параллелепипедов, вложенных друг в друга. Каждый параллелепипед в kd–дереве разбивается плоскостью, перпендикулярной одной из осей координат на два дочерних параллелепипеда. Вся сцена целиком содержится внутри корневого параллелепипеда, но, продолжая рекурсивное разбиение параллелепипедов, можно прийти к тому, что в каждом листовом параллелепипеде будет содержаться лишь небольшое число примитивов. Таким образом, kd– дерево позволяет использовать бинарный поиск для нахождения примитива, пересекаемого лучом.
Построение kd–дерева
Алгоритм построения kd–дерева можно представить следующим образом. Далее по тексту прямоугольный параллелепипед будем называть "бокс" (box).
1) "Добавить" все примитивы в ограничивающий бокс. Т.е построить ограничивающий все примитивы бокс, который будет соответствовать корневому узлу дерева.
2) Если примитивов в узле мало или достигнут предел глубины дерева, завершить построение.
3) Выбрать плоскость разбиения, которая делит данный узел на два дочерних. Будем называть их правым и левым узлами дерева.
4) Добавить примитивы, пересекающиеся с боксом левого узла в левый узел, примитивы, пересекающиеся с боксом правого узла в правый.
5) Для каждого из узлов рекурсивно выполнить данный алгоритм начиная с шага 2. Самым сложным в построении kd–дерева является 3–ий шаг. От него напрямую зависит эффективность ускоряющей структуры. Существует несколько способов выбора плоскости разбиения, рассмотрим их по порядку:
1. Выбрать плоскость разбиения по центру. Самый простой способ – выбирать плоскость по центру бокса. Сначала выбираем ось (x, y или z), в которой бокс имеет максимальный размер, затем разбиваем бокс по центру. Этот способ имеет плохую адаптивность. Интуитивно можно описать причину плохой скорости на таких деревьях тем, что в каждом узле достаточно много пустого пространства, через которое луч трассируется (проходит через дерево во время поиска) в то время как пустое пространство должно сразу же по–возможности отбрасываться.
2. Выбрать плоскость по медиане. Можно подумать, что было бы неплохо разделять узел на два дочерних каждый раз так, чтобы в правом и левом поддереве количество примитивов было одинаково. Таким образом мы построим сбалансированное дерево, что должно ускорить поиск. Однако, все дело в том, что сбалансированные деревья могут помочь только если искомый элемент каждый раз находится в случайном узле, то есть если распределение лучей по узлам во время поиска будет равномерно. В действительности, это не так. Лучей в среднем пойдет больше в тот узел, который больше по своей площади поверхности, а при медианном разбиении эти площади у узлов могут быть разные.
Surface Area Heuristic (SAH)
Введем функцию стоимости прослеживания (cost traversal), которая будет отражать, насколько дорого по вычислительным ресурсам прослеживать данный узел случайным набором лучей. Будем вычислять ее по следующей формуле.
Где CostEmpty – стоимость прослеживания пустого узла (некоторая константа), SurfaceArea – площадь поверхности соответствующего узла, а N – число примитивов в нем. Нужно выбирать плоскость разбиениея так, чтобы минимизировать эту функцию. Аргумент функции x является одномерной координатой плоскости разбиения. Хорошими кандидатами на минимум SAH могут служить границы примитивов. Простой алгоритм построения выглядит следующим образом. Каждый раз при выборе плоскости нужно перебрать всевозможные границы примитивов по трем измерениям, вычислить в них значение функции стоимости и найти минимум среди всех этих значений. Когда мы вычисляем SAH для каждой плоскости, то нам необходимо знать N(left) и N(right) – количества примитивов справа и слева от плоскости. Если вычислять N простым перебором, в итоге получится квадратичный по сложности алгоритм построения.
Surface Area Heuristic порождает более интеллектуальный критерий остановки, чем предел глубины дерева или малое количество примитивов. Если для выбранной плоскости разбиения суммарная стоимость прослеживания дочерних узлов больше, чем стоимость прослеживания текущего узла как листа (то есть по формуле SurfaceArea(Node)*N(Node)), то посторение дерева следует остановить.
Цели дальнейшего исследования
− Разработать модификацию алгоритма трассировки лучей для стереовизуализации;
− Исследовать возможность реализации алгоритма на параллельных архитектурах вычислительных систем, включая архитектуры GPU современных видеокарт ПК;
− Создать прототип программной системы для синтеза реалистичных стереоизображений с использованием метода трассировки лучей на параллельной архитектуре GPU видеокарт ПК, проанализировать характеристики процесса синтеза в сравнении с «классическим» решением задачи.
Выводы
В ходе проведения исследования проблемы были проанализированы существующие подходы к ускорению реализации метода трассировки лучей, выявлены их сильные и слабые стороны, рассмотрены методы создания стерео–изображений. На сегодняшний день реализация трассировки в реальном времени представляется затруднительной.
Однако вычислительные мощности персональных компьютеров и их специализированных подсистем растут каждый день. Трассировка должна вытеснить другие алгоритмы ввиду явного превосходства в качестве изображения и универсальности метода. Следовательно, возможность эффективной по скорости реализации реалистичного синтеза стереоскопических изображений методом трассировки лучей и возможность его реализации на параллельных архитектурах специализированных вычислительных систем является важной задачей.
Литература
1. Михайлюк М.В., Хураськин И.А. Синтез стереоизображения для систем
виртуальной реальности с использованием оптической трекинговой системы. / Программные
продукты и системы, № 3, 2006.
2. «Трехмерная визуализация научной, технической и социальной реальности.
Кластерные технологии моделирования». – Ижевск, 2010.–С.
3. Трассировка лучей, МГУ, 2007. Веб–сайт http://www.ray–tracing.ru/
4. Wald I. Realtime Ray Tracing and Interactive Global Illumination. PhD thesis, Saarland
University, 2004.
5. Shevtsov M., Soupikov A., Kapustin A. Highly Parallel Fast KD–tree Construction for
Interactive Ray Tracing of Dynamic Scenes. In Proceedings of the EUROGRAPHICS conference,
2007.
6. Foley T., Sugerman J. KD–Tree Acceleration Structures for a GPU Raytracer. In
Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hardware, p. 15–
22, 2005.
7. Horn D., Sugerman J., Houston M., Hanrahan P. Interactive k–D Tree GPU Raytracing.
Proceedings of the symposium on Interactive 3D graphics and games on Fast rendering, p. 167–174,
2007.