
|
CV
Biografy
Abstract
|
Theme: Automated subsystem of planning and coordinating the work of commercial agents Aims and objectives The company sells its production to retail outlets (RO). For this purpose, with certain intervals of time commercial agent (CA) visits RO, that he/she is responsible for. Each CA is responsible for 60-100 RO. Each CA is subordinate to his / her supervisor - sales manager (SM), whose task is to define a set of RO, which CA has to visit during the week. About 8-15 CA are under control of one SM. Lets denote a set of RO as ij and a set of CA as Ci. The general scheme of work on present day looks like that:
RO is characterized by a set of parameters: Tij{P,Q,t}. Р – frequency of visiting RO. Q – the importance of visiting the RO at a certain time interval. t – time of a day for visiting RO. Subsystem of scheduling the visits to RO can be represented by the following scheme. 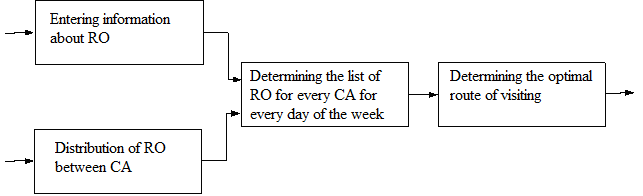
Illustration 1. The general scheme of subsystem’s work Topicality of the work
The solution of the problem of scheduling depends on the problem of determining the list of RO by the following parameters: the time of a visit RO -
tij , frequency of visiting RO - Pij.
Depending on these parameters the number of visits per day can vary because of the changes in the length of the done path. Therefore the topicality of the work lies in identifying the optimal sets of RO for visiting each day of the week. Thus SM has to make sets L{D,T,C} 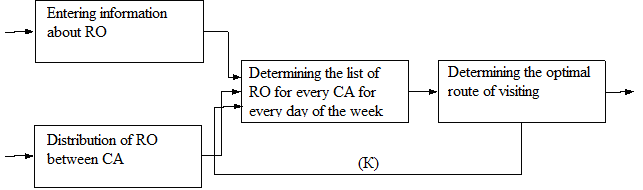
Illustration 2. The general scheme of subsystem’s work after upgrading Thus at the stage of forming a set of RO for visiting L{D,T,C,K} where K – the route’s efficiency factor, SM will be able to take into account the schedule of visiting RO. In this case an already existing subsystem of determining the optimal route by selected points can be the fitness function. 
W – number of working days in a week for the CA. S – the function of determining the length of optimal route by selected RO. Accounting of possible routes and their effectiveness on the stage of forming a set of RO will let increase the efficiency factor of CA, and take into account the requirements for visiting RO, which ultimately will enhance the company's earnings. The main remarkable aspect is the connection of making the optimal schedule’s system with the subsystem of finding the optimal route.
Conclusion At the moment the integration of the subsystem with the corporate database is the most likely direction of development of such systems. This will increase the number of factors taken into account and improve the efficiency of scheduling of visiting retail outlets by commercial agents.
|

