УДК 004.312

 

Источник: 6 международная научно-техническая конференция студентов, аспирантов и молодых ученых "Информатика и компьютерные технологии", 23-25 ноября 2010 года на базе Донецкого национального технического университета.

ОПТИМИЗАЦИЯ ПЛОЩАДИ КРИСТАЛЛА ПРИ РЕАЛИЗАЦИИ УСТРОЙСТВА УПРАВЛЕНИЯ НА CPLD

 

А.В. Хомаха¹, А.С. Лаврик¹, А.А. Баркалов²,

¹ДонНТУ, г.Донецк, ²Зеленогурский университет, Польша.

 

Введение. Известно, что одной из важнейших частей любой цифровой системы является устройство управления (УУ) [1]. В случае представления алгоритма управления в виде линейной граф-схемы алгоритма (ГСА), можно использовать модель композиционного микропрограммного устройства управления (КМУУ) с разделением кодов [2]. В настоящее время для реализации логических схем устройств управления широко используются программируемые логические интегральные схемы (ПЛИС) типа CPLD (Complex Programmable Logic Devices) [4]. Высокая стоимость этого базиса продуцирует актуальную задачу сокращения аппаратурных затрат в схеме. При её решении следует учитывать не только специфику интерпретируемого алгоритма управления, но и особенности элементного базиса. В таком случае, благодаря большому коэффициенту объединения по входу макроячеек ПМЛ, коды классов псевдоэквивалентных операторных линейных цепей (ОЛЦ) могут быть представлены более чем одним источником. В данной работе предлагается метод уменьшения аппаратурных затрат в схеме КМУУ, основанный на использовании двух источников кодов.

 

Основные положения. Пусть ГСА Г представлена КМУУ с разделением кодов   (Рис. 1) .

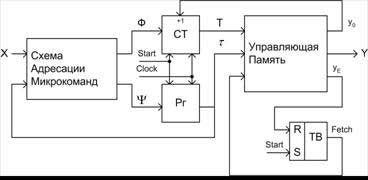
Рисунок 1. Структурная схема КМУУ

В КМУУ , схема адресации микрокоманд (САМ) реализует систему функций возбуждения счётчика CT и регистра Рг. КМУУ  работает следующим образом. По сигналу  начальный адрес (все нули) заносится в Рг и CT. В тоже время, триггер выборки ТВ устанавливается в единичное состояние. При этом , что разрешает выборку микрокоманд из УП. Каждая ячейка УП содержит микрооперации  и специальные переменные  и . Если , то к текущему содержимому СТ прибавляется единица и адресуется следующий компонент текущей ОЛЦ. Иначе – значения СТ и Рг загружаются из САМ. Первый случай соответствует переходу из любого компонента ОЛЦ кроме выхода. Второй случай соответствует переходу из выхода ОЛЦ. Если , триггер выборки обнуляется, сигнал  и работа КМУУ прекращается. Это соответствует переходу из конечной вершины. Отметим, что ОЛЦ  являются псевдоэквивалентными ОЛЦ [4], если их выходы соединены с одной и той же вершиной ГСА Г.

Аппаратурные затраты в логической схеме САМ могут быть уменьшены введением специального блока преобразователя кодов (ПК), преобразующего коды ОЛЦ в коды классов псевдоэквивалентных ОЛЦ [4]. Однако этот блок потребляет некоторые ресурсы микросхемы.

В данной статье предлагается использование свободных ячеек УП для представления кодов классов ПОЛЦ (первый источник), а также использование регистра Рг в качестве второго источника кодов ПОЛЦ.

Основная идея предлагаемого метода. Пусть  будет множеством ОЛЦ, где , если её выход не соединён с конечной вершиной . Пусть  - разбиение множества на классы ПОЛЦ. Закодируем ОЛЦ  таким образом, чтобы большинство классов  было представлено одним интервалом -мерного булева пространства. Для этого может быть использован широко известный алгоритм ESPRESSO [3]. Пусть , где , если класс представлен одним интервалом, иначе .

Если выполняется условие , то регистр Рг является источником всех кодов  для классов . В этом случае САМ реализует  термов, где – число переходов эквивалентного автомата Мили, что является минимально возможным числом переходов [4].

Отметим, что схемы блоков САМ, СТ, Рг и ТВ реализуются на макроячейках ПМЛ. Для реализации УП требуются внешние ППЗУ, имеющие t выходов, где  [2, 3]. При использовании унитарного кодирования микроопераций [4], каждое слово в УП состоит из N+2 бит. Число 2 добавляется к N для учёта дополнительных переменных  и (Рис. 1).

Если каждое ППЗУ имеет t выходов и не менее M слов, то достаточно микросхем для реализации УП, где . Очевидно, что остаётся  свободных выходов микросхем ППЗУ, где . Эти выходы могут быть использованы для кодирования классов , где . Единица добавляется к  для обозначения ситуации . Если выполняется условие , то все классы  могут быть представлены с помощью УП. Иначе может быть представлено лишь  классов, где .Оставшиеся классы  должны быть помещены в  и представлены Рг. В обоих случаях, для интерпретации ЛГСА Г предлагается КМУУ (Рис. 2).

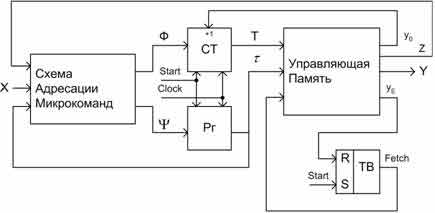
Рисунок 2. Структурная схема КМУУ

 Принципы действия КМУУ  и  практически идентичны.

В работе предлагается следующий алгоритм построения КМУУ :

1. Построение множеств  и  для ЛГСА .

2. Кодирование ОЛЦ  и их компонентов.

3. Построение разбиений  и .

4. Кодирование классов .

5. Построение таблицы переходов КМУУ.

6. Спецификация управляющей памяти.

7. Реализация схемы КМУУ в данном элементном базисе.

Заключение. Предложенный метод направлен на уменьшение числа макроячеек ПМЛ в схеме адресации микрокоманд КМУУ с разделением кодов. Это возможно благодаря таким главным факторам как большой коэффициент объединения по входу современных макроячеек ПМЛ, а также естественная избыточность микросхем ППЗУ, обусловленная тем, что количество их выходов ограничено определённым множеством чисел; существование классов псевдоэквивалентных ОЛЦ.

Исследования показали, что количество макроячеек уменьшается до 12% для КМУУ  в сравнении с эквивалентным КМУУ . Стоит отметить, что данный метод применим лишь для интерпретации линейных ГСА.

Дальнейшие направления наших исследований  связаны с применением предложенного подхода для реализации КМУУ на микросхемах FPGA [3].

 

 

 

Литература

1. Baranov S. Logic Synthesis for Control Automata. – Kluwer Academic Publishers, 1994. – 312 pp.

2. Barkalov A., Titarenko L. Logic Synthesis for Compositional Microprogram Control Units. – Berlin: Springer, 2008. – 272 pp.

3. Maxfield C. The Design Warrior’s Guide to FPGAs. – Amsterdam: Elseveir, 2004. – 541 pp.

4. Соловьев В.В. Проектирование цифровых схем на основе программируемых логических  интегральных схем. – М.: Горячая линия-ТЕЛЕКОМ, 2001. – 636 с.